Назначаем длины участков тихоходного вала в зависимости от крутящегося момента [4 стр. 284]:
f 2 =120мм; e 2 =101мм;.
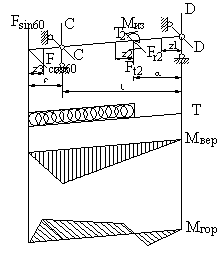 |
1. Определяем реакции опор в вертикальной плоскости из условия равновесия:
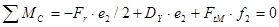 ;
;
откуда
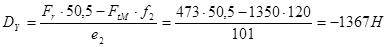 .
.
Условия равновесия:
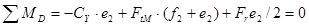 ;
;
откуда
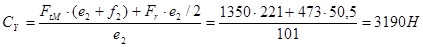 .
.
Выполним проверку из условия равновесия проекций сил на ось Y:
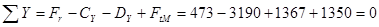 .
.
Реакции С Y и DY найдены верно.
2. Определяем реакции опор в горизонтальной плоскости из условия равновесия:
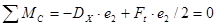 ;
;
откуда
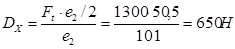
Условия равновесие
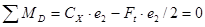 ;
;
откуда
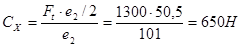
Выполним проверку из условия равновесия проекций сил на ось X:
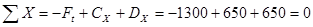 .
.
Следовательно, реакции С X и DX найдены верно.
3. Радиальная нагрузка на опору С
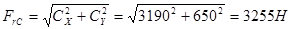 .
.
Радиальная нагрузка на опору D:
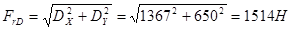 .
.
4. Определяем изгибающие моменты в характерных сечениях вала
(используя формулы сопромата).
а) изгибающий момент в горизонтальной плоскости под подшипником С, D: 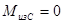 ;
; 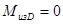
б) изгибающий момент в вертикальной плоскости под подшипником С, D: 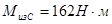 ;
; 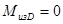
в) изгибающий момент под колесом в горизонтальной и вертикальной плоскостях:
горизонтальная: 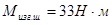 ; вертикальная:
; вертикальная: 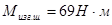
г) изгибающий момент под муфтой в обеих плоскостях: 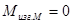
5. Определяем расчетный диаметр вала под подшипником С. Для этого сечения имеем:
Мгор = 0Н·м; Мвер = 162Н·м; Т2=164Н·м;
следовательно 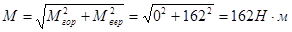 ;
;
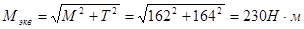 .
.
Тогда
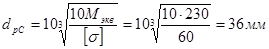 .
.
По ГОСТ 6636-69 принимаем dC = 40мм.
Под подшипником D принимаем такой же диаметр, т.е. dC = dD = d п =40мм.
6. Определяем расчетный диаметр вала под колесом. Для этого сечения имеем:
Мгор = 33Н·м; Мвер = 69Н·м; Т2=164Н·м;
следовательно 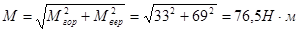 ;
;
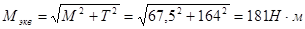 .
.
Тогда
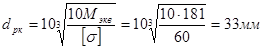 .
.
С учетом ослабление вала шпоночной канавкой, увеличиваем диаметр вала на 10℅. Таким образом, 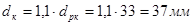 .
.
Полученный диаметр 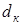 округляем по ГОСТ 6636-69 с таким расчетом, чтобы диаметр под колесом
округляем по ГОСТ 6636-69 с таким расчетом, чтобы диаметр под колесом
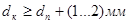 , т.е.
, т.е. 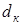
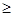 37+2
37+2 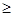 39мм,
39мм,
по ГОСТ 6636-69 принимаем 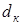 = 42мм.
= 42мм.
7. Диаметр вала под муфту определен [см. п. 5] d м = 35 мм.
Таким образом, для данного вала имеем диаметры: dC= dD= d п = 40мм, dK=42мм, d М = 35мм.
Расчет вала на выносливость
Примем, что нормальные напряжения осей изгиба изменяется по симметричному циклу, а касательные осей кручения – по пульсирующему циклу. Определим коэффициент запаса прочности для опасного сечения вала и сравним с допускаемым значением запаса. Прочность соблюдается при
S > [ S ] = 1,5…2,0.
Коэффициенты запаса определяются по формулам:
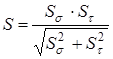 ,
,
где 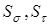 - коэффициенты запаса соответственно по нормальным и касательным напряжениям. Они определяются по формулам:
- коэффициенты запаса соответственно по нормальным и касательным напряжениям. Они определяются по формулам:
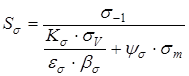 ;
; 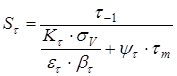 ,
,
где 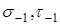 - пределы выносливости материала вала;
- пределы выносливости материала вала; 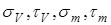 - амплитуда и среднее напряжение циклов нормальных и касательных напряжений. Для симметричного цикла нормальных напряжений
- амплитуда и среднее напряжение циклов нормальных и касательных напряжений. Для симметричного цикла нормальных напряжений 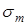 = 0;
= 0; 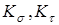 - эффективные коэффициенты концентрации напряжений;
- эффективные коэффициенты концентрации напряжений; 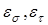 - масштабные факторы;
- масштабные факторы; 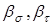 - коэффициенты качества поверхности, принимаем равным единице;
- коэффициенты качества поверхности, принимаем равным единице; 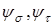 - коэффициенты, учитывающие влияние асимметрии цикла.
- коэффициенты, учитывающие влияние асимметрии цикла.
Проверим на выносливость ведомый (тихоходный) вал, так как крутящий момент этого вала наибольший.
Материал вала – сталь 45, нормализация 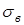 = 570МПа;
= 570МПа; 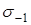 = 246МПа;
= 246МПа;
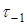 = 142МПа.
= 142МПа.
Рассмотрим сечение под подшипникам на него действуют изгибающие и крутящие моменты. Концентрация напряжений вызвана напрессовкой подшипника.
Суммарный изгибающий момент:
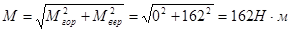 .
.
Моменты сопротивления изгибу и кручению:
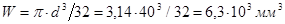 ;
;
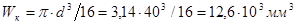 .
.
Коэффициенты понижения пределов выносливости:
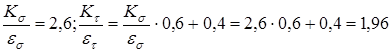
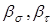 = 1 (шлифование);
= 1 (шлифование); 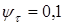 .
.
Амплитуда нормальных напряжений:
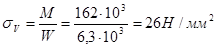 .
.
Амплитуда и среднее напряжение цикла касательных напряжений:
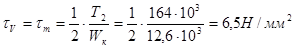 .
.
Определяем коэффициенты запаса прочности:
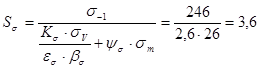 ;
;
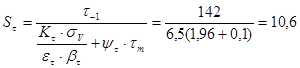 ;
;
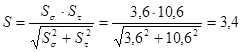 .
.
В рассматриваемом случае условие S > [ S ] = 1,5…2,0 выполняется.
Выбор и расчет подшипников
Дата: 2019-07-24, просмотров: 364.