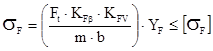Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 (условие работоспособности на изгиб для прямозубых колёс).

    С достаточной степенью точности можно считать, что K_Fb = K_Hb, а K_FV = K_HV.

    Y_F (коэффициент формы зуба) находим в зависимости от числа зубьев рассчитываемого колеса z и коэффициента смещения режущего инструмента x (x₁ = x₂ = 0)

Y_F1 = 4,07; Y_F2 = 3,61.

    На изгибную выносливость проверяются зубья того колеса, для которого отношение 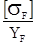 минимально.

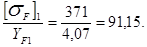
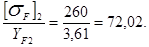
Следовательно, на изгибную прочность проверяем зубья колеса.

s_F2 = 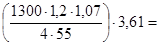26 МПа.

s_F2 = 26 МПа < [s_F]₁ = 260 МПа.

    Проверяем передачу на прочность зубьев при пиковых (кратковременных) перегрузках.

.

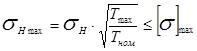s_H =370 МПа, 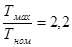, 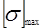=1540 МПа

s_{H max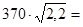} = 550 МПа < [s_H]_max = 1540 МПа.

Следовательно, контактная пластическая деформация зубьев (бринеллирование) будет отсутствовать.

s_{F max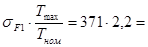} = 816 < [s_F]_max = 900 МПа.

Следовательно, объёмная пластическая деформация будет отсутствовать.

 

Геометрические характеристики зацепления

 

Определяются только те геометрические характеристики, которые необходимы при вычерчивании зубчатого зацепления передачи и рабочих чертежей зубчатых колёс.

Расчёт геометрических размеров передачи внешнего зацепления производится по ГОСТ 16532-70.

Некоторые размеры и параметры передачи уже определены.

m_n = 4 мм; a_w = 160 мм; b₁ = 60 мм; b₂ = 55 мм; d₁ = 72 мм; d₂ = 252 мм; u = 3,5.

Диаметры окружностей выступов

d_a1 = d₁+2·(h 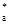+x₁)· m_n; d_a2 = d₂+2·(h 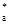+x₂)· m_n.

h 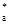= 1 (коэффициент высоты головки зуба исходного контура).

x₁ = x₂ = 0 (коэффициенты смещения режущего инструмента).

d_a1 = 72+2·(1+0)·2 = 76 мм;

d_a1 = 252+2·(1+0)·2 = 256 мм.

    Диаметры окружностей впадин зубьев

d_f1 = d₁-2·(h 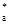+c^*-x₁)· m_n; d_f2 = d₂-2·(h 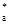+c^*-x₂)· m_n.

c^* = 0,25 (коэффициент радиального зазора исходного контура).

d_f1 = 72-2·(1+0,25-0)·2 = 67 мм;

d_f2 = 252-2·(1+0,25-0)·2 = 247 мм.

 

Ориентировочная оценка КПД редуктора

 

Для одноступенчатого редуктора h_ред = h_пер = 1-y_з-(y_n+y_r).

y_з = 2,3·f· 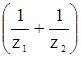 (коэффициент, учитывающий потери в зацеплении; по данной зависимости определяется при x₁ = x₂ = 0).

f = (0,06…0,1) (коэффициент трения в зубчатом зацеплении).

Принимаем f = 0,07.

y_з = 2,3·0,07· = 0,0115.

y_n – коэффициент, учитывающий потери в подшипниках.

y_r – коэффициент, учитывающий потери на разбрызгивание и перемещение масла (гидравлические потери).

(y_n+y_r) = 0,15…0,03.

Так как передача имеет невысокую окружную скорость (V = 2,8 м/с), принимаем (y_n+y_r) = 0,03. h_ред = 1-0,01-0,03 = 0,96.

    Теоретическое определение потерь крайне затруднено, поэтому на практике КПД редукторов определяют на натуральных объектах, пользуясь специальными испытательными установками.

 

Определение усилий, действующих в зацеплении

 

Окружная сила F_t = 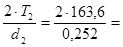1300 Н.

Осевая сила F_a = F_t·tgb = 0, так как b = 0°.

Радиальная сила F_r = 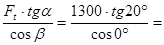473 Н.

Расчёт ремённой передачи

1. Размер сечения выбираем по рекомендации [1, с. 152] в зависимости от T_эд и n_эд.

T_эд = 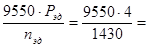26,7 Н·м.

Принимаем клиновой ремень нормального сечения типа А.

2. Назначаем расчётный диаметр малого шкива d_{р1 min}. По рекомендации [1, с. 151] для ремня сечения А имеем d_{р1 min} = 90 мм.

    Следует применять шкивы с большим, чем d_{р min} диаметром. По ГОСТ 20889-75 – ГОСТ 20897-75 принимаем

d_р1 = 100 мм.

3. Определяем расчётный диаметр большего шкива

d_р2 = (1-e)·d_р1·u_рем.

e = 0,02 (коэффициент скольжения).

d_р2 = (1-0,02)·100·2 = 196 мм.

Полученный диаметр округляем до стандартного ближайшего значения по ГОСТ 20897-75

d_р2 = 200 мм.

Уточняем передаточное число

u_рем = 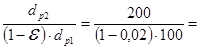2,04.

4. Определяем межосевое расстояние.

Минимальное межосевое расстояние

a_min = 0,55·(d_р1+d_р2)+h.

h = 8 мм (высота профиля ремня для сечения А).

a_min = 0,55·(100+200)+8 = 173 мм.

a_max =2·(100+200) = 600 мм.

    Для увеличения долговечности ремней принимают a > a_min. Причём a назначается в зависимости от передаточного числа u_рем и расчётного диаметра d_р2. По рекомендации [1, с. 153] при u_рем = 2 имеем 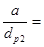1,2.

a = 1,2·d_р2 = 1,2·200 = 240 мм. Учитывая компоновку привода, принимаем окончательное межосевое расстояние a = 430 мм.

5. Определим длину ремня

.

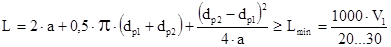V₁ – скорость ремня, равная окружной скорости малого шкива.

V₁ = 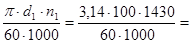7,5 м/с.

L_min = 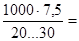(375…250) мм.

L = 2·200+0,5·3,14·(100+200)+ 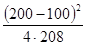= 884 мм.

L > L_min, следовательно ремень будет иметь достаточную долговечность.

    Полученную длину L округляют до стандартного ближайшего значения по ГОСТ 1284.3-80.

    Принимаем L = 900 мм, что находится в рекомендуемом стандартном диапазоне для ремня типа А.Учитывая изменение межосевого расстояния (a=430 мм), полученное при компоновке общего вида привода к горизонтальному валу, получим окончательную длину ремня L = 1250 мм.

6. Уточняем межосевое расстояние передачи

a = 0,25·[L-D₁+ 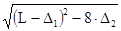], где

D₁ = 0,5·p·(d_р1+d_h2) = 0,5·3,14·(100+200) = 471 мм,

D₂ = 0,25·(d_р1-d_р2)² = 0,25·(200-100)² = 2500 мм².

a = 0,25·[1250-471+ ] = 390 мм.

Округляем полученное значение до ближайшего из стандартного ряда чисел a = 430 мм.

    Принимаем угол обхвата на малом шкиве

.

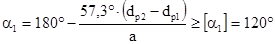a₁ = 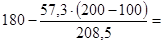152° > [a₁] = 120°.

Следовательно, угол обхвата на малом шкиве имеет достаточную величину.

7. Допускаемая мощность, которую передаёт ремень в заданных условиях эксплуатации

[P] = (P₀·C_a·C_L+10^-4·DT_и·n₁) ·C_р.

Определим P₀ – номинальную мощность, которую передаёт ремень в определённых условиях (a₁ = 180°, u = 1, V = 10 м/с, длина ремня L₀, спокойная нагрузка)

P₀ = 1,3.

Значения коэффициентов C_a, C_L, DT_и, C_р, C_z

C_a = 0,95 (коэффициент, учитывающий влияние на тяговую способность угла обхвата).

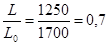
C_L = 0,95 (коэффициент, учитывающий реальную длину ремня).

DT_и = 1,1 (поправка к моменту на быстроходном валу).

C_р = 0,95 (коэффициент, учитывающий режим работы передачи, в данном случаи для односменной работы).

[P] = (1,3·0,95·0,95+10^-4·1,1·1430) ·0,95 = 1,19 кВт.

8. Необходимое количество ремней с учётом неравномерности нагрузки на ремни

.

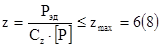C_z = 0,9 (коэффициент, учитывающий неравномерность распределения нагрузки между одновременно работающими ремнями).

z = 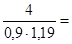3,7.

Принимаем z = 4, что меньше z_max = 6. Следовательно, передача будет иметь допустимое число ремней.

9. Сила предварительного натяжения одного ремня

.

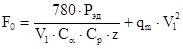q_m = 0,105 кг/м (масса одного метра длины ремня).

F₀ = 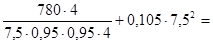121 Н.

10. Нагрузка на валы передачи

F_рем = 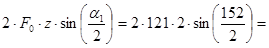940 Н.

Угол между силой и линией центров передачи

Q = 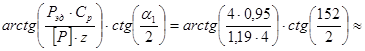10°.

Если Q 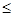 20°, то с достаточной степенью точности можно принимать, что F_рем направлена по линии центров передачи.

11. Проверяем частоту пробегов ремней на шкивах

n_n = 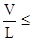[n_n] = 10 с^-1.

n_n = 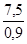=8,3 с^-1 < [n_n].

12. Размеры шкивов клиноремённых передач регламентированы ГОСТ 20889-80 – ГОСТ20897-80, размеры профиля канавок регламентированы ГОСТ 20898-80.

Расчёт муфт

 

Для соединения отдельных узлов и механизмов в единую кинематическую цепь используются муфты, различные типы которых могут также обеспечить компенсацию смещений соединяемых валов (осевых, радиальных, угловых и комбинированных), улучшение динамических характеристик привода, ограничение передаваемого момента и прочее.

Наиболее распространённые муфты стандартизированы или нормализованы. Выбор муфт проводится в зависимости от диаметра вала и передаваемого крутящего момента.

1. Определяем расчётный момент муфты

T_рм = k·T_м, где T_м – номинальный момент на муфте (T_м = T₂ = 163,6 Н·м), k – коэффициент режима работы.

    Принимаем, что поломка муфты приводит к аварии машины без человеческих жертв.

k = k₁·k₂.

k₁ = 1,2 (коэффициент безопасности; поломка муфты вызывает аварию машины).

k₂ = 1,3 (коэффициент, учитывающий характер нагрузки; нагрузка с умеренными толчками).

k = 1,2·1,3 = 1,56.

T_рм = 1,56·163,6 = 255,2 Н·м.

2. Муфта выбирается по каталогу таким образом, чтобы выполнялось условие T_рм 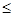T_табл.

    Из упругих компенсирующих муфт наибольшее применение имеют следующие: муфта упругая втулочно-пальцевая типа МУВП по ГОСТ 21424-75 и муфта с резиновой звёздочкой по ГОСТ 14084-76.

    По рекомендации [5, с. 303, с. 304] принимаем муфту упругую втулочно-пальцевую МУВП-40 по ГОСТ 21424-75, так как она обладает большими компенсирующими возможностями и принятая муфта имеет меньшие габариты (тип 2 – на короткие концы валов).

 T_рм 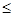T_табл = 400 Н·м.

3. Определяем силу F_rм действующую со стороны муфты на вал, вследствие неизбежной несоосности соединяемых валов.

F_rм = (0,2…0,3)·F_tм, где F_tм – окружная сила на муфте, F_tм = .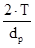

    Для МУВП d_р = D₁ – диаметр окружности, на которой расположены центры пальцев.

d_р = D₁ = 242 мм.

    Окружная сила на муфте

F_tм = 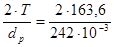= 1350 Н.

    Следовательно, нагрузка от муфты на вал

F_rм = (0,2…0,3)·1350 = (270…405) Н.

Принимаем F_rм = 338 Н.

4. Проверяем возможность посадки муфты на вал редуктора. Определяем расчётный диаметр вала в месте посадки муфты

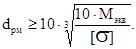
    В данном случае M_гор = 0; M_верт = 0,5·F_rм·f₂.

f₂ = 10+110 = 120 мм. (расстояние от стенки редуктора до муфты или длина полумуфты).

M_верт = 0,5·338·0,12 = 20,28 Н·м.

    Суммарный изгибающий момент

M = 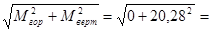20,28 Н·м.

    Эквивалентный момент

M_экв = 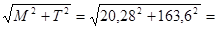165 Н·м.

    Допускаемые напряжения [s] = 55…65 МПа, принимаем [s] = 55 МПа.

    Расчётный диаметр вала в месте посадки муфты

d_рм = 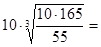31,1 мм.

    С учётом ослабления вала шпоночной канавкой имеем

d_рм = 1,1·d_рм = 1,1·31,1 = 34 мм.

Окончательно принимаем d_рм =35 мм.

Таким образом, муфта проходит по посадочному диаметру вала и в дальнейших расчётах диаметр вала под муфту принимается d_м = 35 мм.

Расчет валов

 

Исходные данные: крутящий момент на быстроходном (входном) валу редуктора T ₁ = 48,19 Н∙м; крутящий момент на тихоходном (выходном) валу редуктора T ₂ = 164 Н∙м; окружная сила в зубчатом зацеплении F_{t 1} = F_{t 2} = 1300 Н; радиальная сила в зубчатом зацеплении F_{r 1} = F_{r 2} = 473 Н; ширина шестерни b ₁ = 60 мм; ширина колеса b ₂ = 55 мм; делительный диаметр шестерни d ₁ = 72 мм; делительный диаметр колеса d ₂ = 252 мм; сила, действующая на вал, от натяжения ремней F _рем = 940 Н; дополнительная сила, действующая со стороны муфты, на вал F_{r м} = 1350 Н.