| Система | ||
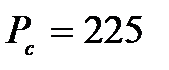 МВт МВт
| 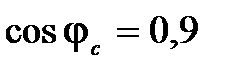
| 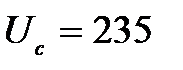 В В
|
| Генератор | ||
 МВА МВА
| 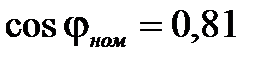
| 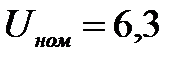
|
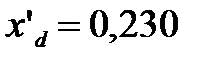
| 
| 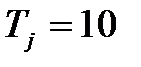
|
| Трансформатор Т -1 | ||
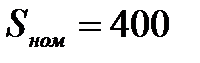 МВА МВА
| 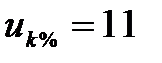
| 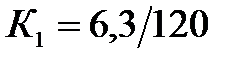
|
| Трансформатор Т -2 | ||
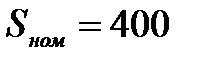 МВА МВА
| 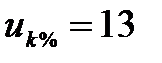
| 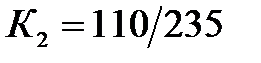
|
| ЛЭП | ||
|
| 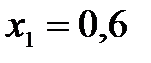 Ом/км Ом/км
| |
| Нагрузка | ||
|
| 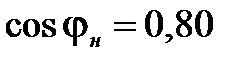
| |
| Вид КЗ | ||
| К2 | ||
Требуется:
определить предельное время отключения КЗ, проведя расчет приближенно без учета активных сопротивлений и зарядной мощности линий. Принять, что переходная ЭДС при нарушении режима неизменна.
Решение
Расчет проведем в относительных единицах. За базисные величины примем
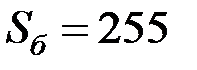 МВА; Uб = 105 кВ.
МВА; Uб = 105 кВ.
1. Приводим исходные параметры к базисным величинам:
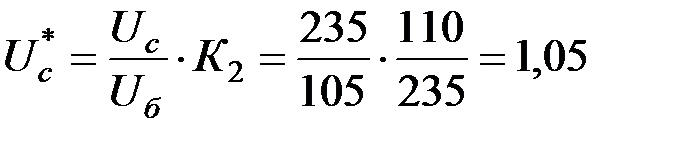 .
.
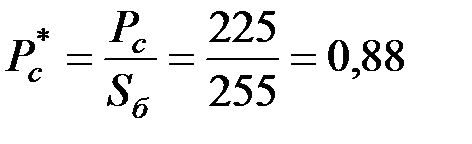 .
.
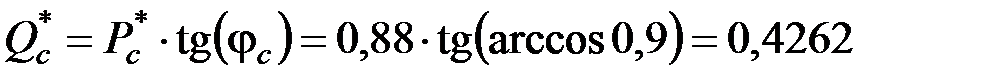 .
.
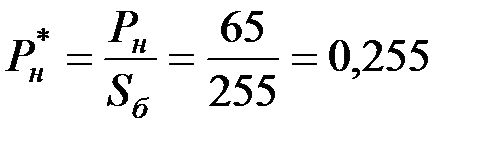 .
.
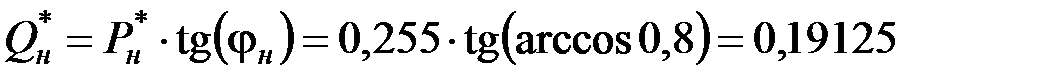 . (6.14)
. (6.14)
Приводим параметры элементов электропередачи к базисным условиям и базисной ступени 110 кВ.
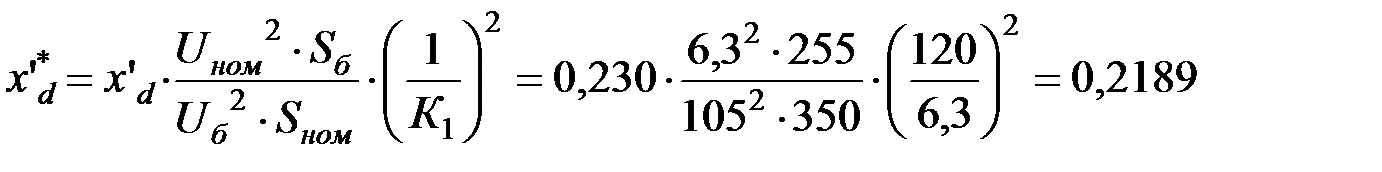 .
.
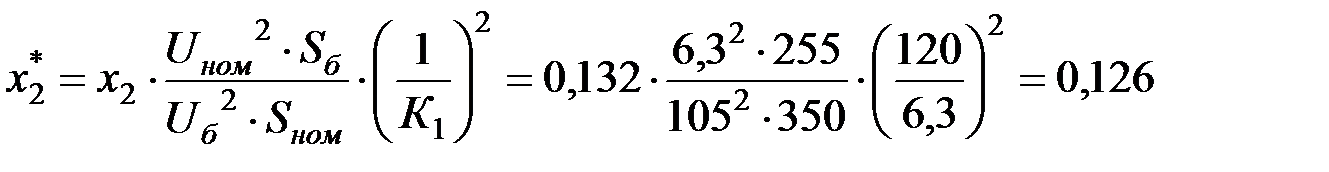 .
.
 .
.
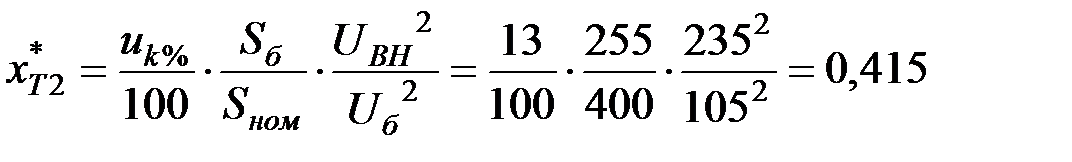 .
.
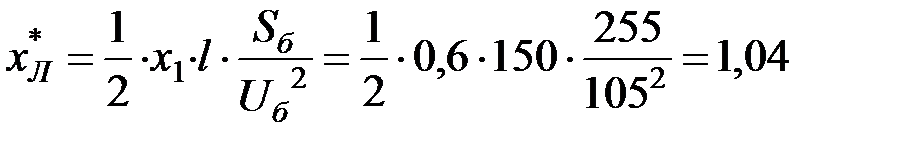 .
.
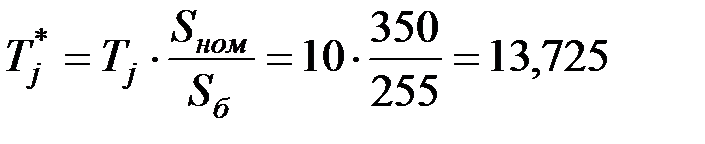 .
.
В дальнейших расчетах опускаем знак «звездочка» (*), так как расчет будет только в относительных единицах (о.е.).
Составим схему замещения для нормального режима и определим ЭДС генератора за переходным реактивным сопротивлением (рис. 6.10).
Рис. 6.10. Схема замещения для нормального режима
2. Рассчитаем нормальный режим работы электропередачи.
Суммарное сопротивление между шинами генератора и шинами бесконечной мощности определяется:
 .
.
Напряжение на шинах генератора:
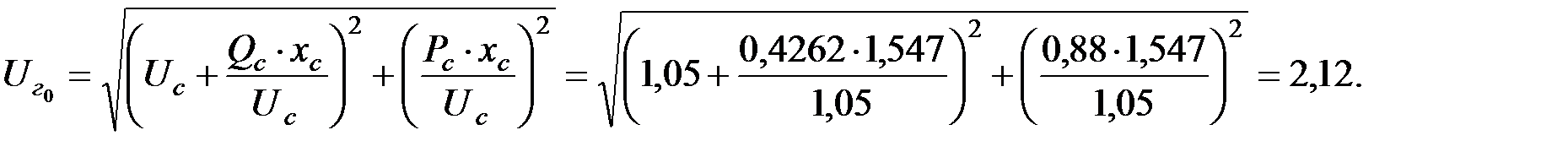
Из формулы (6.22) определим угол нагрузки 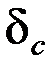 .
.
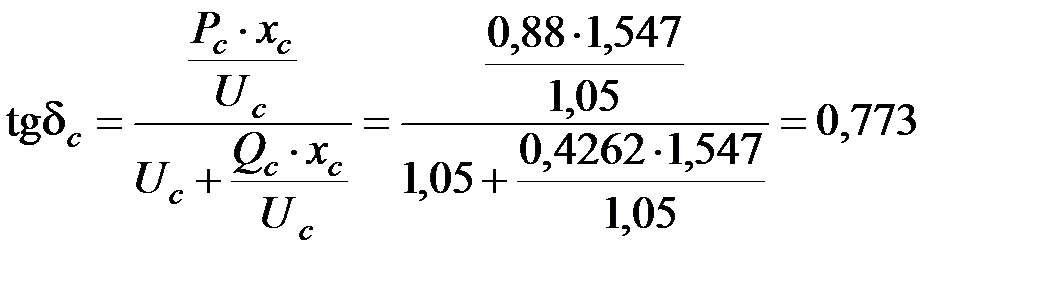 .
.
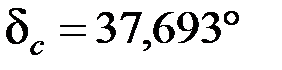 .
.
Посчитаем сопротивление нагрузки:
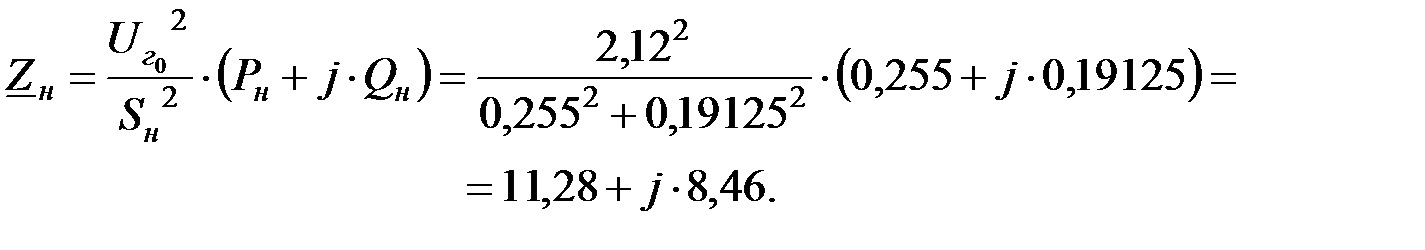
Определим потери реактивной мощности в сети до шин генераторного напряжения:
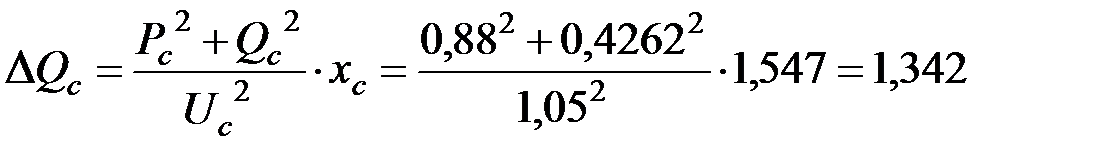 .
.
Тогда мощность, отдаваемая генератором, получится:
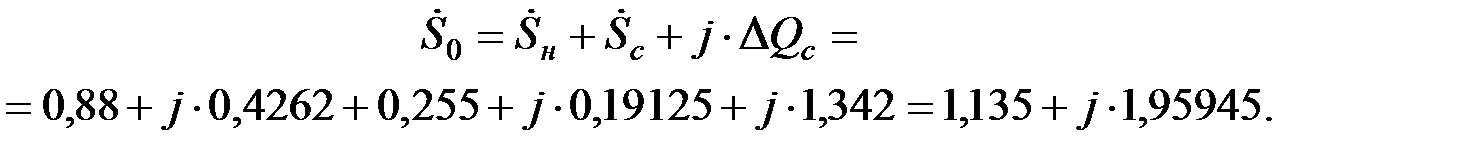
ЭДС за переходным сопротивлением генератора будет равна:
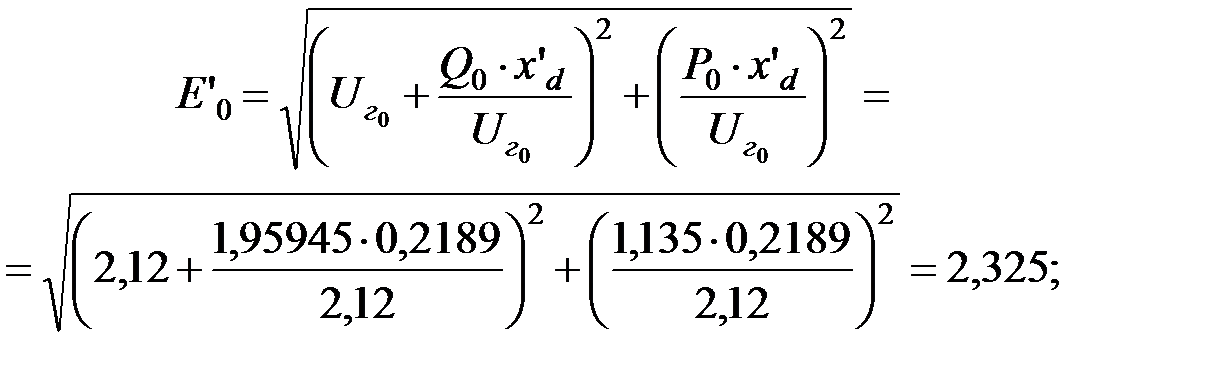
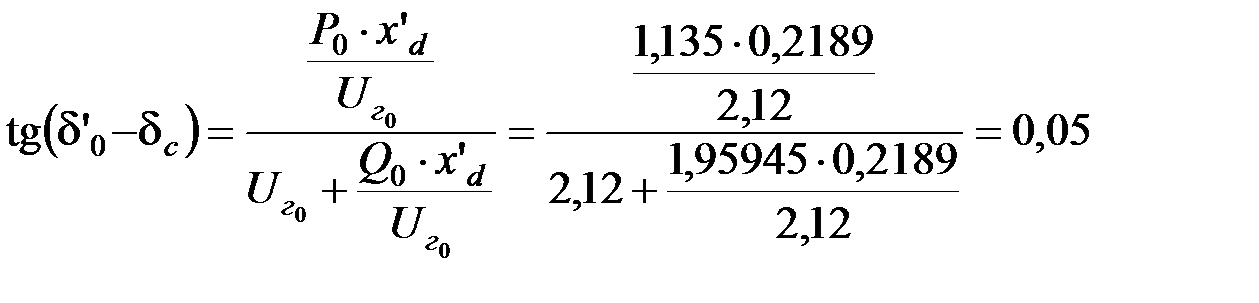 ;
;
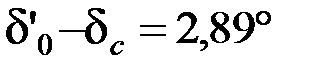 .
.
Тогда угол между ЭДС E’0 и напряжением Uc
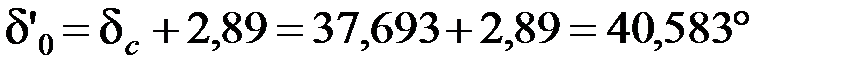 .
.
Определим собственные и взаимные проводимости схемы замещения методом преобразования (рис. 6.11).
Рис. 6.11. Схема замещения в нормальном режиме с учетом сопротивления нагрузки
Собственная проводимость:
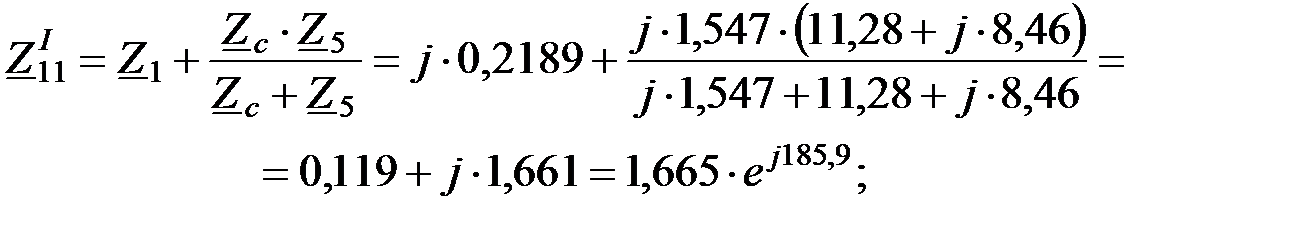
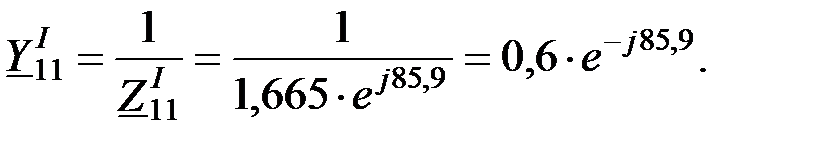
Находим дополнительный угол:
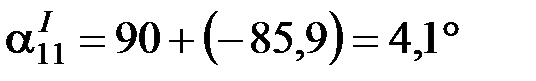 .
.
Взаимная проводимость:
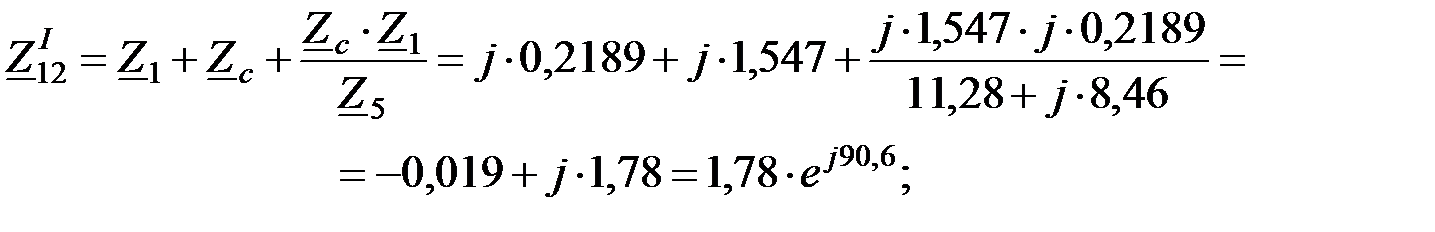
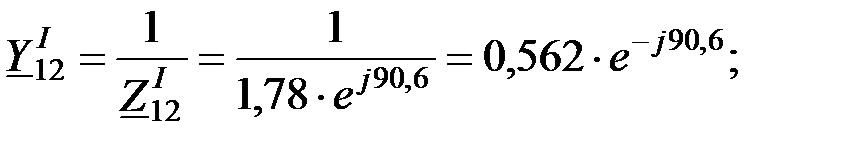
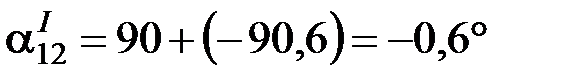 .
.
3. Рассчитаем аварийный режим.
Схема замещения электропередачи для прямой последовательности в режиме двухфазного короткого замыкания отличается от схемы замещения в нормальном режиме включением в точку КЗ аварийного шунта, сопротивление которого равно результирующему сопротивлению обратной последовательности. Значения сопротивлений элементов электропередачи для токов обратной последовательности приведены на рис. 6.12, где сопротивление нагрузки принято равным 0,35 от сопротивления прямой последовательности, а x’d заменяется на x2.
Рис. 6.12. Схема замещения обратной последовательности
Результирующее сопротивление схемы для токов обратной последовательности относительно точки КЗ
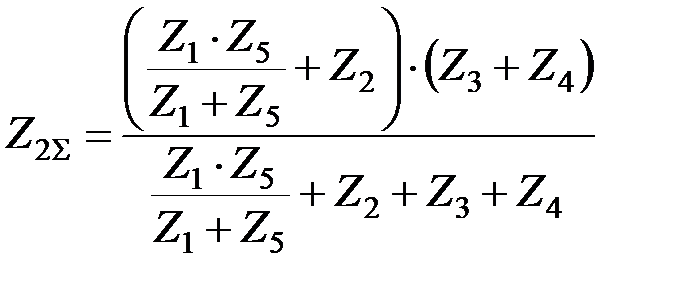 ;
;
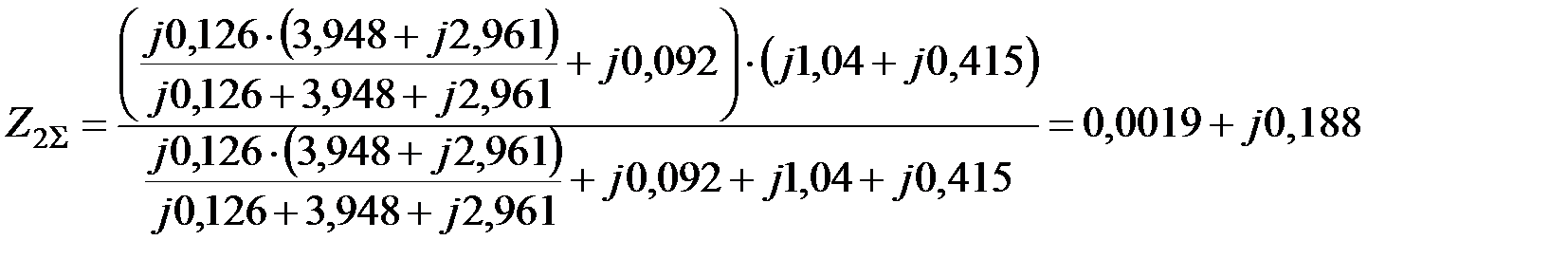 .
.
Результирующее сопротивление аварийного шунта в точке короткого замыкания равно (рис. 6.13):
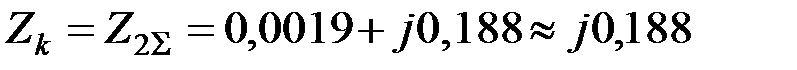 .
.
Рис. 6.13. Эквивалентная схема аварийного режима
Методом единичных токов найдем собственные и взаимные проводимости.
Пусть ток в сопротивлении Z4 равен единице:
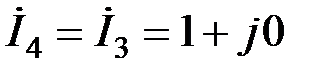 .
.
Напряжение в точке b будет:
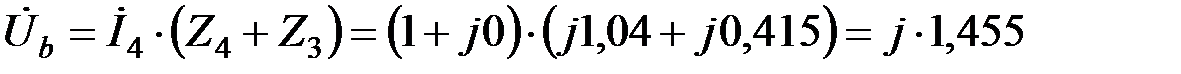 .
.
Ток, протекающий по аварийному шунту, составит:
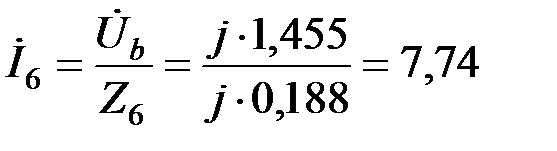 .
.
Ток и падение напряжения на сопротивлении ветви 2 определим по формуле
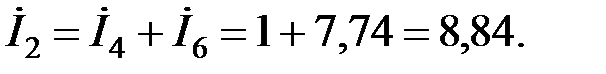
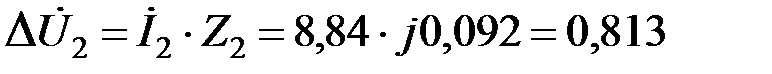 .
.
Напряжение в точке a
 .
.
Ток в ветвях 5 и 1 соответственно
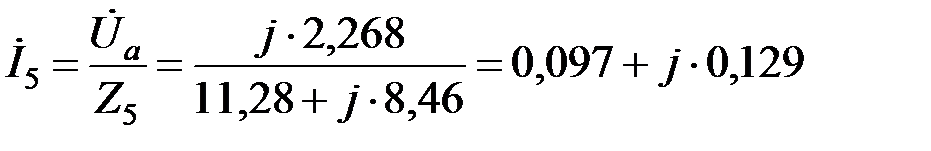 .
.
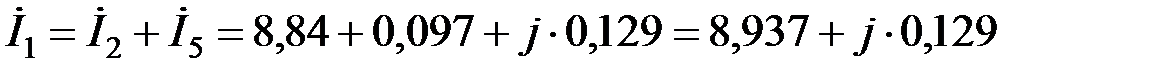 .
.
Падение напряжения на сопротивлении в ветви 1
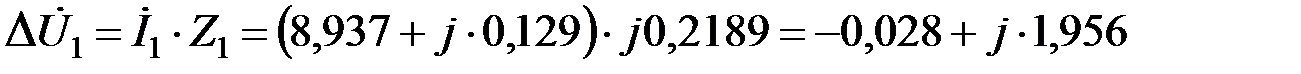 .
.
ЭДС в точке подключения передающей станции
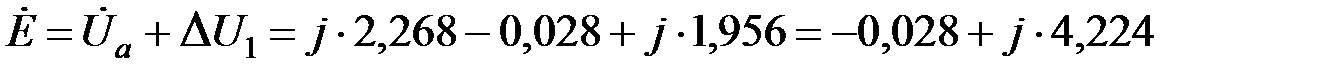 .
.
Собственная проводимость схемы короткого замыкания относительно передающей станции
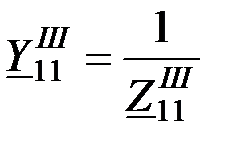 ,
,
где 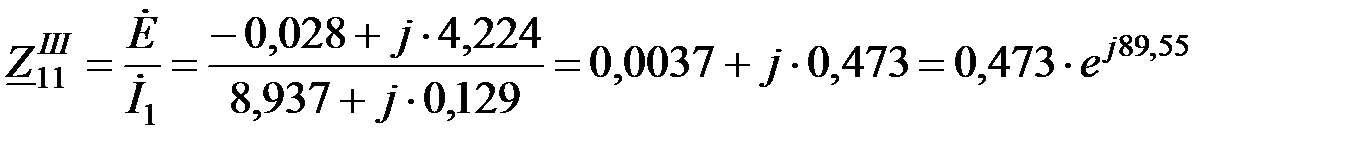 .
.
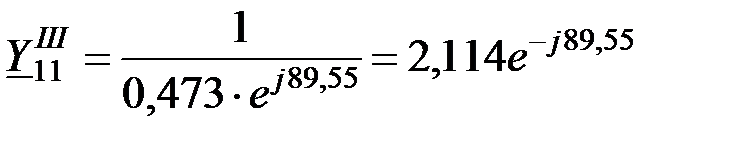 .
.
Дополнительный угол составит
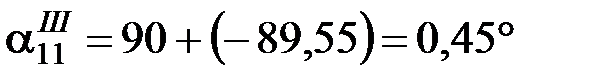 .
.
Взаимная проводимость схемы короткого замыкания:
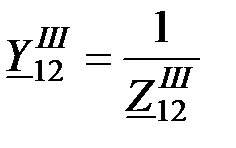 ,
,
где 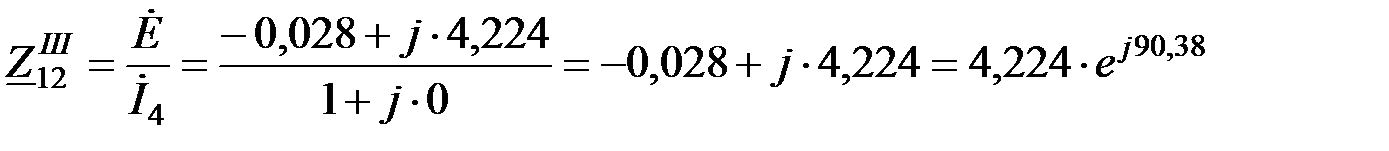 .
.
 .
.
Дополнительный угол
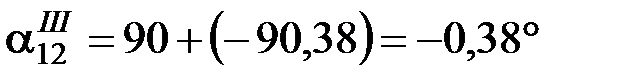 .
.
4. Послеаварийный режим
В схеме замещения электрической цепи для послеаварийного режима (рис. 6.14) аварийный шунт отключен, сопротивление линии электропередачи увеличено вдвое. Собственные и взаимные проводимости для нее определяются так же, как и для схемы нормального режима.
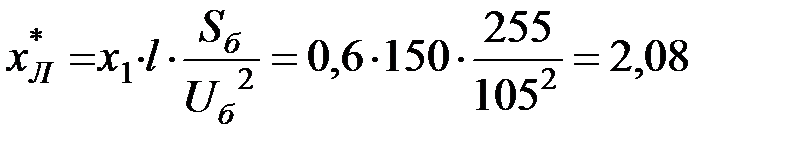 .
.
Рис. 6.14. Схема замещения послеаварийного режима
Суммарное сопротивление между шинами генератора и шинами бесконечной мощности:
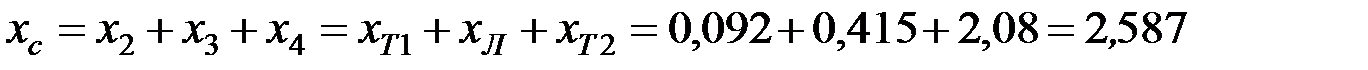 .
.
Напряжение на шинах генератора:

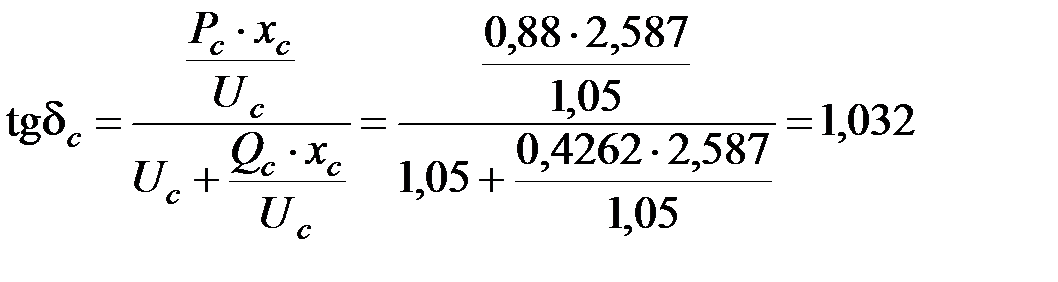 ;
;
 .
.
Сопротивление нагрузок:
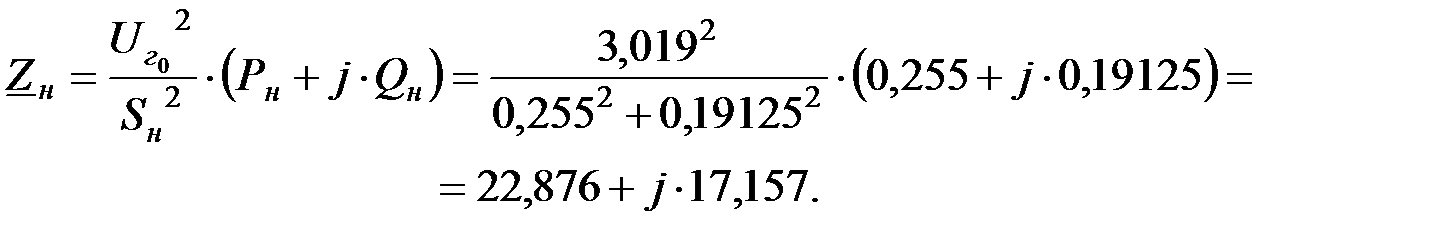
Потери реактивной мощности:
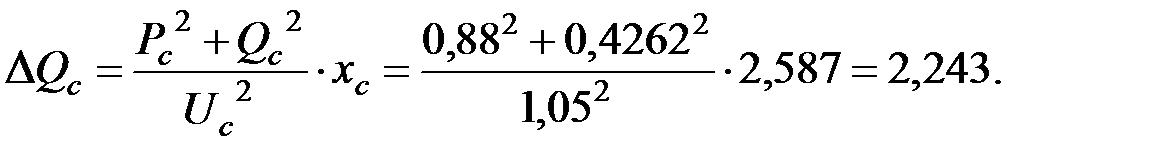
Мощность, отдаваемая генератором:
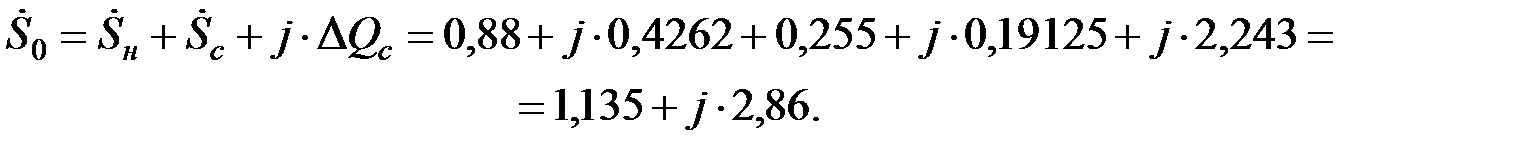
ЭДС за переходным сопротивлением генератора:
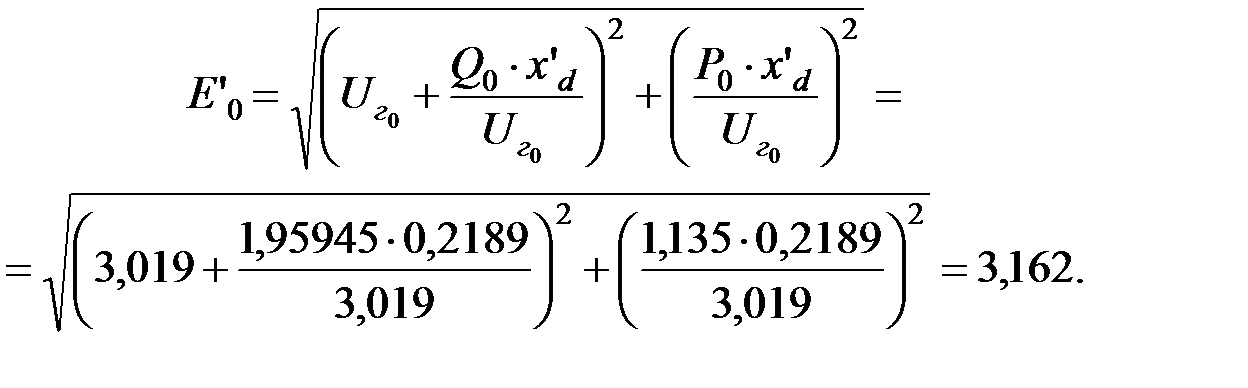
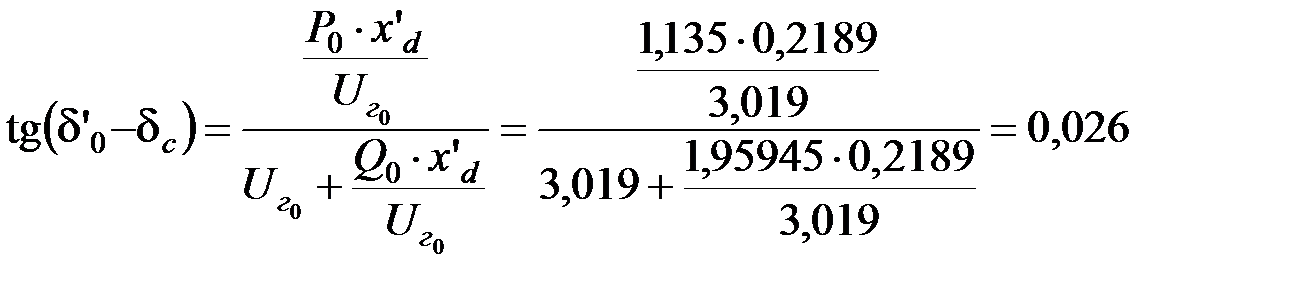 .
.
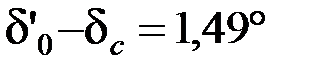 .
.
Угол между ЭДС E’0 и напряжением Uc
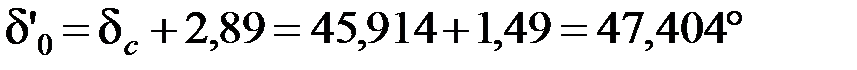 .
.
Собственная проводимость
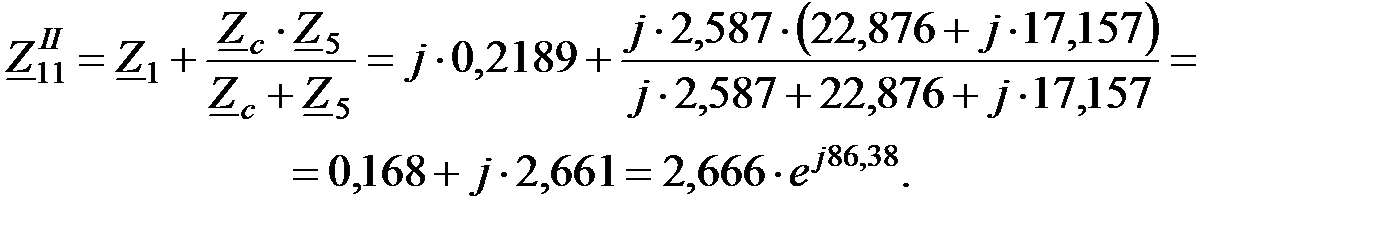
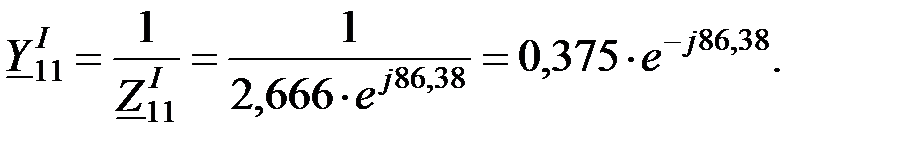
Находим дополнительный угол:
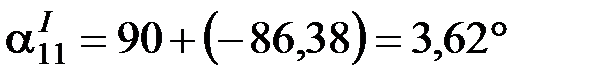 .
.
Взаимная проводимость


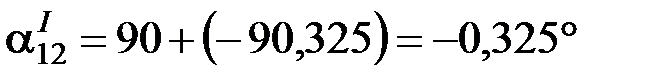 .
.
4. Характеристики электрической мощности генератора передающей станции для различных режимов найдем из следующих выражений:
а) нормальный режим:
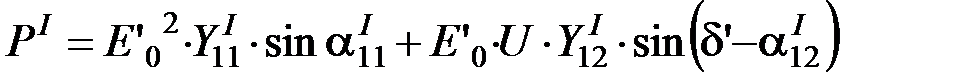 ;
;
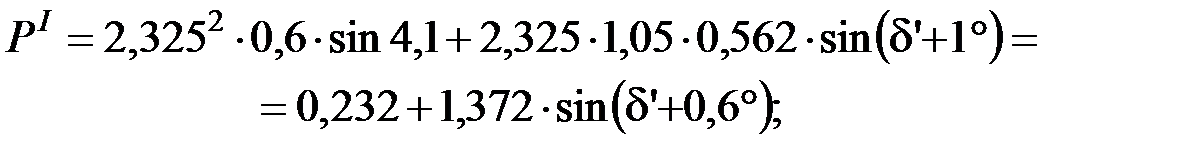
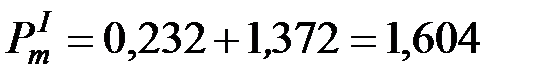 ;
;
б) аварийный режим (двухфазное КЗ):
 ;
;

 ;
;
в) послеаварийный режим:
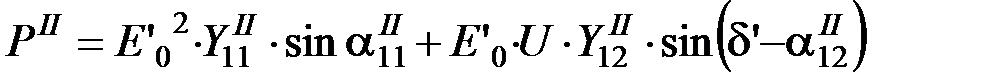 ;
;
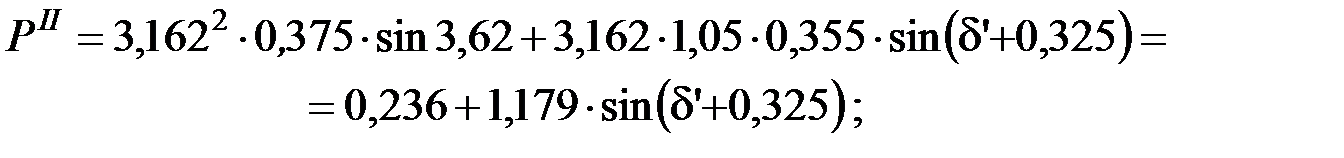
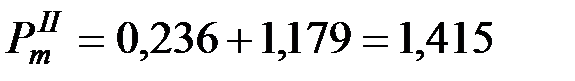 .
.
Построим полученные характеристики (см. рис. 6.15).
Из условия равенства площадок ускорения и торможения определим предельный угол отключения короткого замыкания. В соответствии с выражением
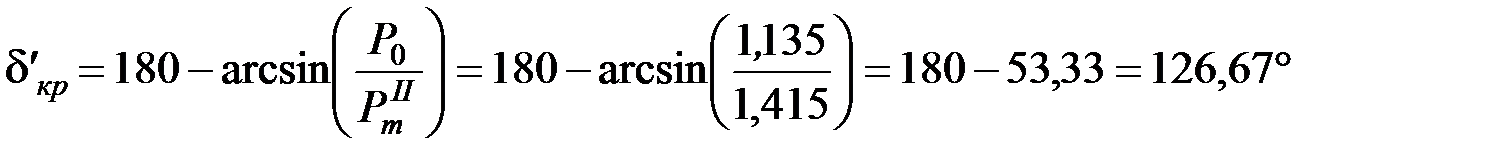
получим
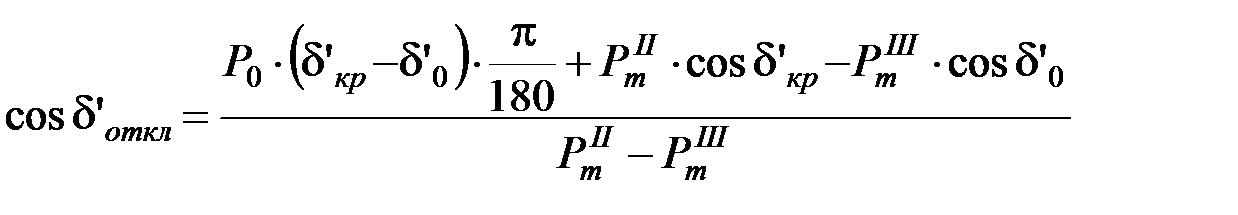 ;
;

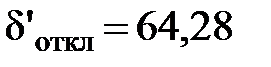 .
.
| P |
Рис. 6.15. Угловые характеристики передаваемой мощности разных режимов с площадками ускорения и торможения
Чтобы найти предельное время отключения короткого замыкания, необходимо построить зависимость 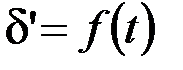 , которая может быть определена из уравнения движения ротора. Решим это уравнение методом последовательных интервалов (численное интегрирование).
, которая может быть определена из уравнения движения ротора. Решим это уравнение методом последовательных интервалов (численное интегрирование).
Длительность расчетных интервалов  примем равной 0,05 с.
примем равной 0,05 с.
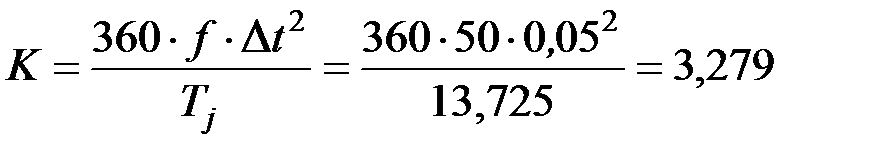 .
.
Первый интервал (0–0,05 с).
Электрическая мощность, отдаваемая генераторами в первый момент до возникновения КЗ
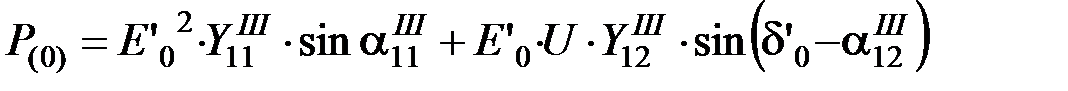 ;
;
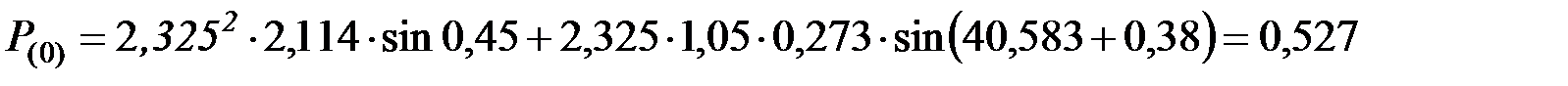 .
.
Избыток мощности в начале интервала
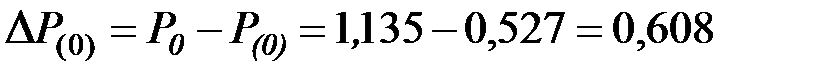 .
.
Приращение угла за интервал
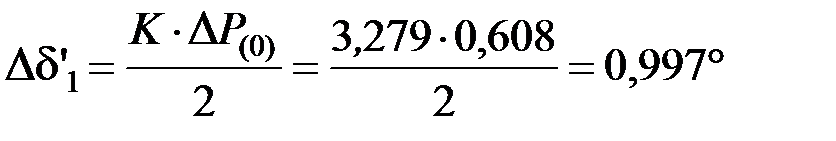 .
.
Угол к концу первого интервала
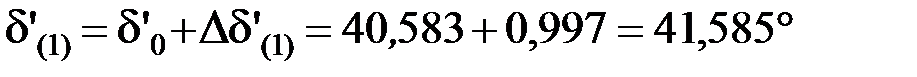 .
.
Второй интервал (0,05–0,1 с).
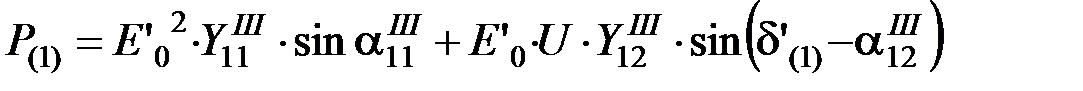 .
.
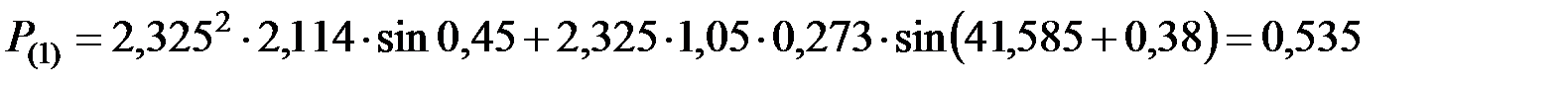 .
.
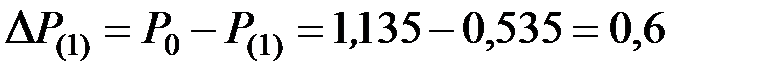 .
.
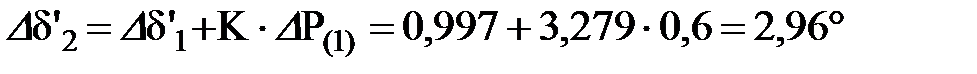 .
.
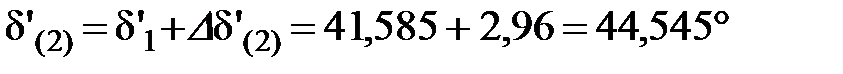 .
.
Третий интервал (0,1–0,15 с).
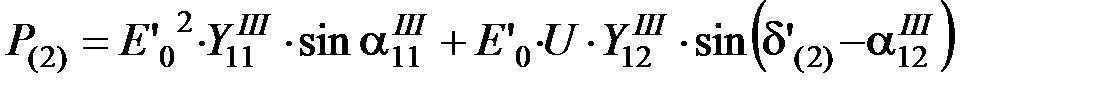 .
.
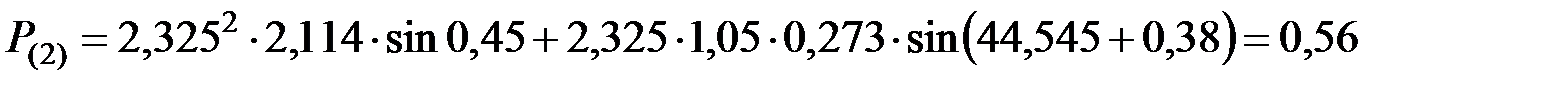 .
.
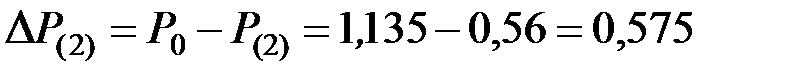 .
.
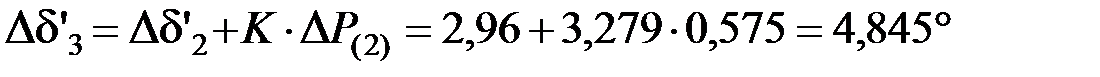 .
.
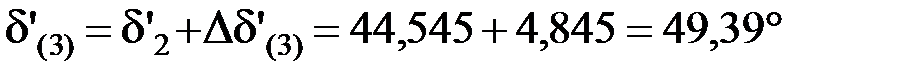 .
.
Дата: 2019-07-24, просмотров: 449.
 км
км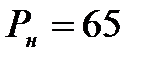 МВт
МВт