Задача динамической устойчивости – анализ характера процесса и расчет всех или части параметров режима при переходе системы от одного режима к другому. К задачам этого вида относится расчет динамического перехода от начального установившегося режима к новому установившемуся режиму, наступающему при случайном отключении части элементов системы (отключение группы генераторов, линии передачи, нагрузки и т. д.) или при отключении их после аварии (обычно короткого замыкания) в одном из этих элементов. Практические расчеты в этом случае обычно ведутся с учетом основных нелинейностей и динамических характеристик. Наиболее распространенным методом количественного исследования является метод численного интегрирования системы дифференциальных уравнений, позволяющий выявить изменение параметров режима во времени и в конечном счете по виду этих зависимостей сделать заключение об устойчивости перехода системы от одного режима к другому, или, как иначе говорят, о динамической устойчивости системы [1, 2]. 

Вернемся к простейшей схеме энергосистемы (рис. 2.7) и рассмотрим на примере отключения одной из цепи ЛЭП передачу электроэнергии от станции Г на шины энергосистемы С бесконечной мощности (U_с = const) (рис. 4.1). 

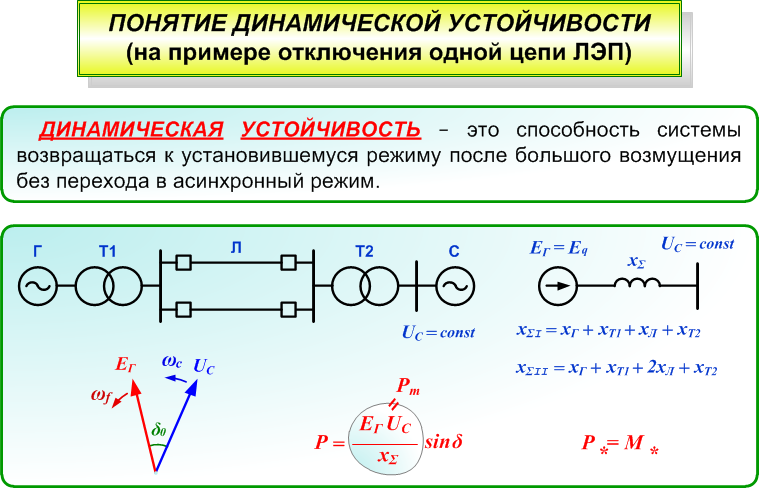
Рис. 4.1. Модель энергосистемы при отключении одной из цепей ЛЭП: х_ΣI – эквивалентное сопротивление передачи в нормальном режиме (две цепи ЛЭП работают);
х_ΣII – эквивалентное сопротивление передачи в послеаварийном режиме (одна цепь ЛЭП выведена из работы)

Мощность, выдаваемая генератором в систему, равна мощности турбины и обозначена P₀, угол генератора – δ₀. Характеристика мощности, соответствующая нормальному (доаварийному) режиму, определяется по формуле

.

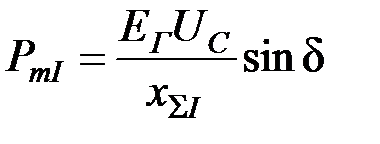В результате отключения одной цепи ЛЭП меняется сопротивление передачи с х_ΣI на большую величину х_ΣII (рис. 4.2)_, так как сопротивление ЛЭП выросло в 2 раза. Это вызовет уменьшение максимума характеристики мощности послеаварийного режима

.

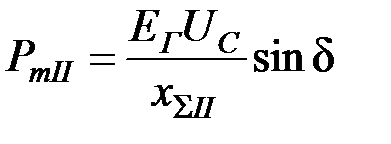а                                                                             б

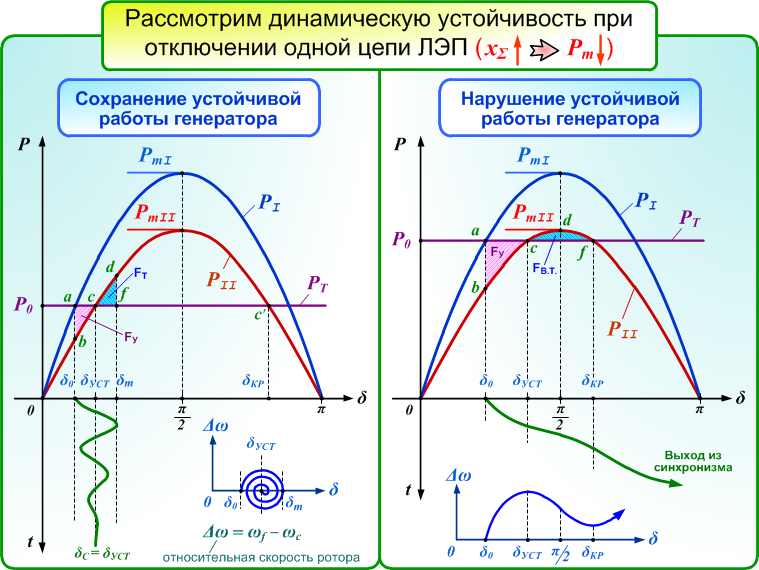
Рис. 4.2. Динамический переход из нормального режима в послеаварийный: а – вариант сохранения динамической устойчивости; б – выход из синхронизма

На рис. 4.2 показаны два варианта развития событий в энергосистеме при отключении одной цепи ЛЭП. В первом случае (рис. 4.2, а) устойчивость системы сохранится, во втором (рис. 4.2, б) – произойдет выход генератора из синхронизма, т. е. устойчивость не сохранится. Рассмотрим первый случай.

После внезапного отключения линии происходит переход с характеристики мощности P_mI на характеристику P_mII. Из-за инерции ротора угол не может измениться мгновенно, поэтому рабочая точка перемещается из точки а в точку b.

На валу, соединяющем турбину и генератор, возникает избыточный момент, определяемый разностью мощности турбины, которая не изменилась после отключения линии, и новой мощности генератора (ΔР = Р₀ – Р₍₀₎).

Под влиянием этой разности ротор машины начинает ускоряться, двигаясь в сторону больших углов δ. Это движение накладывается на вращение ротора с синхронной скоростью, и результирующая скорость вращения ротора будет ω = ω₀ + ∆ω, где ω₀ – синхронная скорость вращения; ∆ω – относительная скорость. В результате ускорения ротора рабочая точка начинает движение по характеристике P_mII. Мощность генератора возрастает, а избыточный (ускоряющий) момент (пропорциональный разности ΔР = Р₀ – Р₍₀₎ – убывает. Относительная скорость ∆ω возрастает до точки с.

В точке с избыточный момент становится равным нулю, а скорость ∆ω – максимальной. Движение ротора со скоростью ω не прекращается в точке с, ротор по инерции проходит эту точку и продолжает движение. Но избыточный момент при этом меняет знак и начинает тормозить ротор. Относительная скорость вращения начинает уменьшаться и в точке d становится равной нулю. Угол δ в этой точке достигает своего максимального значения. Но и в точке d относительное движение ротора не прекращается, так как на валу агрегата действует тормозной избыточный момент, поэтому ротор начинает движение в сторону точки с, относительная скорость при этом становится отрицательной. Точку с ротор проходит по инерции, около точки b угол становится минимальным, и начинается новый цикл относительного движения. Колебания угла δ (t) показаны на рис. 4.2.
Затухание колебаний объясняется потерями энергии при относительном движении ротора.

В тот период движения, когда избыточный момент ускоряет вращение ротора, кинетическая энергия, запасенная ротором в период его ускорения, будет определяться по формуле:

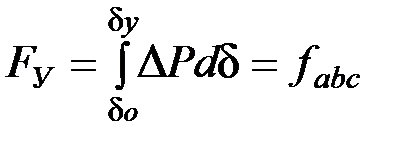,                                  (4.1)

где f_abc – заштрихованная площадь abc на рис. 4.2.

Изменение кинетической энергии в период торможения вычисляется как

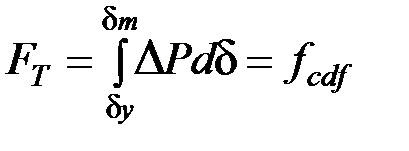.                            (4.2)

Площади f_abc и f_cdf, пропорциональные кинетической энергии ускорения и торможения, называются площадями ускорения и торможения. В период торможения кинетическая энергия ротора переходит в потенциальную энергию, которая возрастает с уменьшением скорости ∆ω. В точке d кинетическая энергия равна нулю, и для определения максимального угла отклонения ротора δ_m достаточно выполнить условие:

.

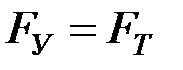Отсюда следует, что при максимальном угле отклонения δ_m площадь ускорения должна быть равна площади торможения («правило площадей»).

Максимально возможная площадь торможения 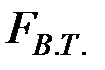 определяется
углом δ_кр. Если максимальный угол превысит значение δ_кр, то на валу «турбина – генератор» возникнет ускоряющий избыточный момент
(Р₀ > Р_Г) и генератор выпадет из синхронизма (рис. 4.2, б).

Таким образом, рассчитать динамическую устойчивость – это значит определить условия, при которых она обеспечивается. В частности, для генератора определить предельную мощность, развивая которую в исходном режиме, он сохранит устойчивость при отключении одной из цепей ЛЭП.