Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

В разд. 1.1 отмечена особенность электроэнергетической отрасли, которая заключается в единстве процесса производства, передачи и потребления. Из данного определения становится понятно, что технологически это неразрывно связанные процессы. Никто не будет строить новые дополнительные мощности, новые электрические станции, если в этом нет нужды производства.

В экономическом плане источники и потребители тоже связаны, например, в настоящее время по росту потребления электроэнергии можно оценить рост производства, или его снижение при уменьшении потребления электрической энергии.

На заре возникновения и распространения электричества, производство электроэнергии представляло собой механическое вращение электрического генератора, который вырабатывал электрический ток. Через провода электрическая энергия подавалась на двигатель, и он вращался.
То есть сначала механическая энергия превращалась в электрическую, затем снова – в механическую. Тогда это показывали как эксперимент, который вызывал восторг у зрителей. Сегодня электроэнергетическая отрасль значительно выросла и по мощностям и по охвату территорий снабжения электрической энергии, и не видно, как ежедневно происходит этот процесс, потребитель привык, да и многое для него просто не видно.
Специалисты же должны понимать, как влияют источники и потребители электрической энергии друг на друга в вопросе их устойчивости.

Так, например, качество работы ЭЭС определяется двумя главными показателями: частотой электрического тока ЭЭС и напряжениями в узлах нагрузки. Частота, поддерживаемая в системе на заданном уровне, зависит от баланса активных мощностей Р (см. подразд. 2.1–2.3). Уровни напряжения в узлах – от баланса реактивных мощностей Q. Нарушение баланса по реактивной мощности приводит к изменению уровня напряжений.

Разберем все по порядку. Узлом нагрузки называется совокупность потребителей электроэнергии, подключенных к центру питания, под которым понимаются шины источника (станции, подстанции) различного напряжения 0,4; 6; 10 кВ и т. д.

В узлах нагрузки сосредоточены различные потребители: освещение, двигатели, обогрев, преобразователи и пр. Всю нагрузку можно разделить на двигательную и статическую. У двигательной нагрузки могут возникать проблемы с устойчивостью работы, у статической нагрузки таких проблем нет. Однако статическая нагрузка оказывает влияние на переходные процессы и знание её характеристик также необходимо. Поэтому рассмотрим  устойчивость двигательной нагрузки, в которой наиболее распространенным является асинхронный двигатель (АД).

Схема замещения асинхронного двигате­ля (АД) приведена на рис. 3.6, а. Она состоит из ряда элементов: х_к – сумма индуктивного сопротивления обмотки статора х₁ и приведенного к статору индуктивного сопротивления обмотки ротора х’₂; х_μ – сопротивление ветви намагничивания; r’₂ – активное сопротивление ротора, приведенное к обмотке статора, при стоящем двигателе; U – напряжение; s – скольжение. Для определения потребляемой асинхронным двигателем актив­ной и реактивной мощности воспользуемся Г-образной (упрощенной) схемой замещения (рис. 3.6, б), в которой ветвь намагничивания, потребляющая относительно небольшой ток, вынесена на вход двигателя [3].

 

         а                                                                    б

 

Рис. 3.6. Схемы замещения АД, питающегося от мощной системы:
а – Т-образная; б – Г-образная

 

АД имеет ряд параметров. Скольжение АД – отношение скорости вращения поля ро­тора относительно поля статора и определяется по формуле

 

s = 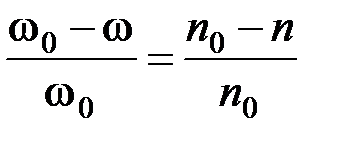,                                  (3.3)

 

где w₀ и w – синхронная частота вращения (частота вращения поля статора) и реальная частота вращения ротора, 1/c; n₀ и n – механическая номинальная и реальная скорости вращения, об/мин.

Для схемы замещения рис. 3.6, б активная мощность Р, потребляемая двигателем, определяется выражением

 

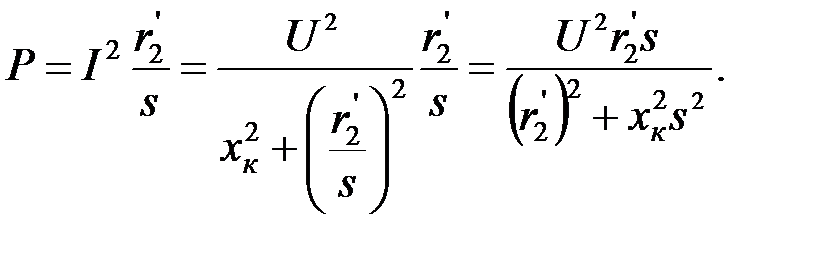           (3.4)

 

По формуле (3.4) можно определить максимум этой характеристики, для чего приравняем к нулю производную от мощности по скольжению 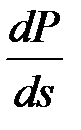 = 0. Проведя необходимые преобразования, получим

 

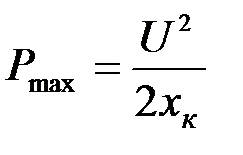  при 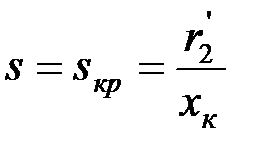,                         (3.5)

 

где s_кр – критическое скольжение, которое соответствует максимальной мощности. 

Реактивная мощность Q, потребляемая двигателем, определяется по формуле

 

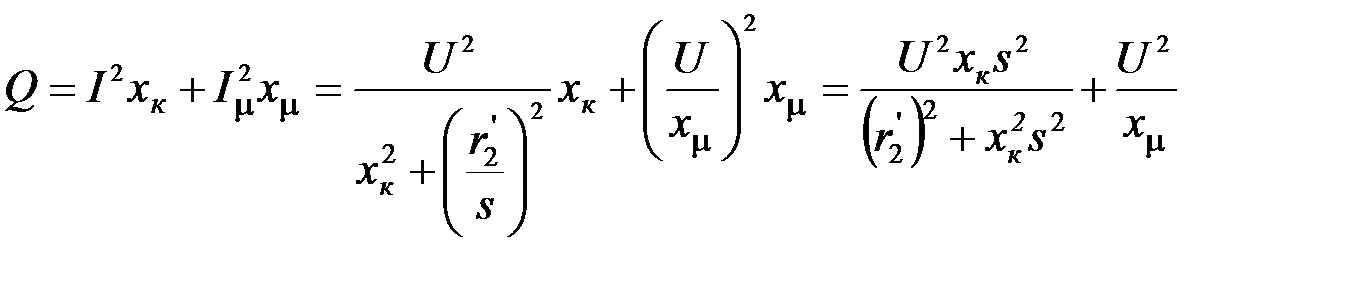
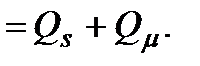 (3.6)

 

Таким образом, суммарная реактивная мощность, потребляемая двигателем из сети, состоит из двух составляющих: первая Q_s отражает зависимость реактивной мощ­ности рассеяния от напряжения и скольжения, вторая Q_μ – зависимость реактивной мощности на­магничивания от напряжения.

Рис. 3.7. Характеристики реактивной мощности АД

Мощность Q_s при уменьшении напряжения увеличивается за счет более заметного увеличения скольжения. При скольжении больше критического (s > s_кр » 0,2), что имеет место при напряжении (0,6–0,7)U_ном, двигатель интенсивно затормаживается и
останавливается (опрокидывается). Мощность Q_μ при изменении напряжения изменяется по квадратичной зависимости (рис. 3.7). 

На основании (3.4) или (3.5) построим харак­теристику мощности (момента) АД
(рис. 3.8).

 

 

Рис. 3.8. Режимы работы асинхронного двигателя: а – статически устойчивый; б – статически неустойчивый

Рассмотрим случай, когда момент сопротивления механизма не зависит от скорости вращения двигателя. В этом случае характеристика механизма будет изображаться прямой, параллельной оси абсцисс.

Способность двигателя самостоятельно возвращаться к исходному режиму работы после малых возмущений называют статической устойчивостью двигателя. Определим формальные (практические) критерии статической устойчивости двигательной на­грузки.

Рассмотрим сначала характеристики системы «асинхронный двигатель – механизм». В этой системе вращающий электромагнитный момент создаётся двига­телем, а механический момент сопротивления – приводимым в движение механизмом.

Точки пересечения характеристик двигателя и механизма являются точками, где возможен установившийся режим, так как действующие на валу агрегата моменты уравновешены. Однако только в одной из этих точек режим системы будет устойчив.

Предположим, что при работе системы в точке а двигатель по какой-либо причине притормозился, то есть произошло небольшое увеличение скольжения. Тогда электромагнитная мощность возрастёт, двигатель уско-рится, скольжение уменьшится, и система вернется к режиму в точке а.

Иное положение создаётся при работе в точке б. Здесь любое малое возмущение вызовет либо торможение вплоть до остановки, либо переход в режим, соответствующий точке а.

Из всех режимов, лежащих левее и ниже точки а и левее и выше точки б, двигатель будет стремиться перейти в точку устойчивого равновесия а. Из режимов, лежащих правее и ниже точки б, двигатель будет стремиться в сторону увеличения скольжения (уменьшения скорости) вплоть до полной остановки. Отсюда можно сделать вывод, как и в случае синхронного двигателя, что все режимы, соответствующие точкам, лежащим на восходящей части характеристики двигателя, могут быть реализованы, все режимы на нисходящей части неустойчивы.

Условие устойчивой работы можно записать в виде

.

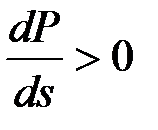При 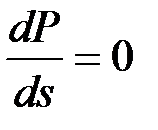 имеем граничный режим, при  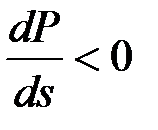режим работы будет неустойчивым.

Таким образом, режим работы асинхронного двигателя устойчив, если производная от мощности двигателя по скольжению больше нуля. Этот критерий удобно применять для анализа режимов, связанных с увеличением нагрузки двигателя.

Однако нарушение статической устойчивости может произойти и при снижении напряжения питания.

Характеристики асинхронного двигателя при разных величинах напряжения на его зажимах показаны на рис. 3.9. Приводимый во вращение механизм имеет не зависящую от скорости вращения характеристику.

 

 

Рис. 3.9. Характеристики мощности асинхронного двигателя и механизма

 

При снижении напряжения на зажимах двигателя увеличивается скольжение, двигатель начинает тормозиться, но мощность, развиваемая двигателем, остается не­изменной до тех пор, пока максимальная электромагнитная мощность не станет равной мощности меха­низма (напряжение, соответствующее такому режиму, называют критическим U _кp). Как только это случится, двига­тель будет тормозиться до полной остановки (опрокинется), поскольку мощность двигателя окажется меньше мощности механизма.

Условие нарушения устойчивой работы можно в этом случае записать в виде (см. рис. 3.7):

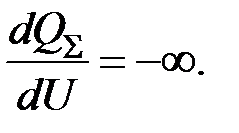
В соответствии с формулой (3.4) зависимость P(U) имеет квадратичный характер, поэтому снижение максимума активной мощности двигателя при снижении напряжения превосходит в относительных единицах снижение напряжения.

Изменения активной и реактивной мощностей асинхронного двигателя при сни­жении напряжения на его зажимах хорошо видны на
рис. 3.10. Активная мощность не изменяется вплоть до момента опрокидывания (при этом незначительно возрастает скольжение). Реактивная мощность в процессе опрокидывания двигателя резко увеличивается. После остановки двигателя суммарная реактивная мощность при снижении напряжения уменьшается.

 

 

Рис. 3.10. Зависимость активной и реактивной мощностей АД при измене­нии уровня напряжения

 

Рассмотрим режимы работы двигателя на границе устойчивости.
При равенстве максимальной мощности двигателя P_мах и мощности механизма Р₀ происходит опрокидывание двигателей, т. е. нарушение их
устойчивой работы. Этот процесс начинается при равенстве нулю производной .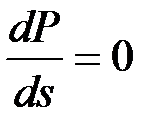

Как было показано выше, по формуле максимальной мощности (3.5) при Р_max = Р₀ получим 

 

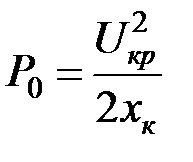,                                         (3.6)

 

откуда

 

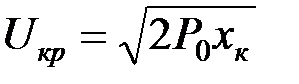.                                     (3.7)    

 

Таким образом, определены параметры АД и критерии, которые влияют на его статическую устойчивость.

 

Практические критерии

  статической устойчивости узла нагрузки

 

Статическая устойчивость узла нагрузки определяется, прежде всего, свойствами двигательной нагрузки, то есть свойствами синхронных и асинхронных двигателей, так как именно их работа может быть нарушена в результате возмущений нормального режи­ма. Но необходимо учитывать и статическую нагрузку (освещение, обогрев и т. п.).

Рис. 3.11. Статические характеристики комплексной нагрузки по напряжению

Устойчивость нагрузки можно оценить, используя статические характеристики нагрузки (рис. 3.11).

Статические характеристики – это зависимости, проявляющиеся в установившихся режимах, при медленных изменениях режима. Динамические характеристики проявляются в переходных процессах при быстрых изменениях параметров режима [3].

Для расчетов режимов и устойчивости электрических систем обычно используют статические характеристики нагрузки, под которыми понимают зависимости активной и реактивной мощностей нагрузки от напряжения и частоты питающей сети:

P_н = F(U, f); Q_н = F(U, f).

Статические характеристики узла нагрузки можно получить расчетным или экспе­риментальным путем. Трудность определения характеристик расчетным путем состоит в получении достоверных исходных данных.

Статические характеристики нагрузки, содержащие в своём составе асинхронные двигатели, показаны на рис. 3.11. Видно, что при снижении напряжения реактивная мощность сначала уменьшается, а потом начинает возрастать. Уменьшение peaктивной мощности объясняется уменьшением тока намагничивания АД. Последующее увеличение потребляемой мощности при снижении напряжения обусловлено увеличивающимся скольжением АД.

Если обратиться к схеме замещения АД (рис. 3.6), можно видеть, что при резком увеличении скольжения, которое происходит при остановке двигателя, сопротивление 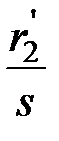 увеличивается, что приводит к возрастанию тока в цепи рассеяния. Точка, в которой 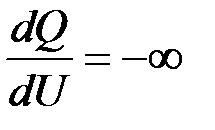, соответствует моменту опрокидывания двигателя (рис. 3.7).

Рис. 3.12. Схема замещения при питании нагрузки от одного источника

Если нагрузка питается от шин по­сто­ян­но­го напряжения Е через линию сопротивлением х_вн (рис. 3.12), то признаком нарушения устойчивости будет соотношение

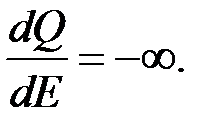
Связь между U и Е может быть представлена в виде

 

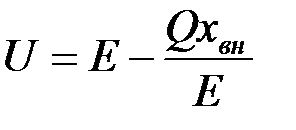.              (3.8)

 

Дифференцируя по Е, получим:

 

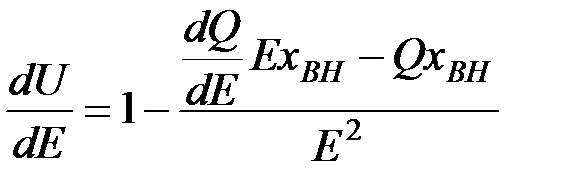.                           (3.9)

 

Отсюда при 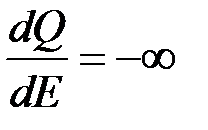 имеем 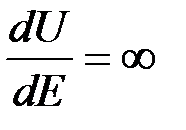 или 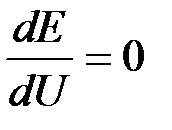. Следовательно, равенство  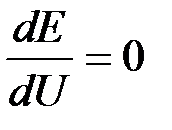соответствует моменту опрокидывания двигателей.
До момента опрокидывания .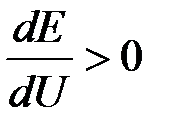

Таким образом, критерий устойчивости комплексной нагрузки можно сформулировать как положительность производной от ЭДС источника питания по напряжению в узле нагрузки:

.

Рис. 3.13. Определение Uкр с помощью критерия

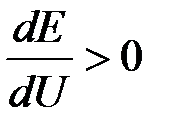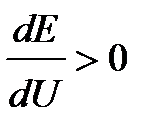
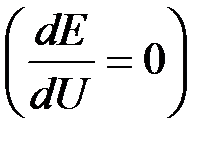Рассматриваемый критерий используется обычно для расчётов устойчивости нагрузки, получающей питание от одного источника. Задаваясь различными значениями напряжения на нагрузке U, определяют по статическим характеристикам нагрузки величины Р_н и Q_н. Затем подсчитывают ЭДС Е источника питания и строят характеристику E = f(U) (рис. 3.13). Минимум характеристики  даёт значение критического напряжения комплексной нагрузки U_кр.

В тех случаях, когда комплексная нагрузка питается от нескольких
источ­ников, удобнее использовать другой критерий устойчивости.

На рис. 3.14 показаны зависимости суммарной реактивной мощности, генерируемой различными источниками Q_ΣГ, и суммарной реактивной мощности, потребляемой нагрузкой Q_ΣН, от напряжения на нагрузке U.

 

 

Рис. 3.14. Статические характеристики генераторов Q_ΣГ и нагрузки Q_ΣН

 

Зависимость суммарной реактивной мощности, потребляемой нагрузкой, от шин с напряжением U представляет собой обычную статическую характеристику Q_H = f(U). Характеристика Q_ΣГ = f(U) вычисляется при неизменных ЭДС Е источников в зависимости от напряжения на нагрузке и при условии, что суммарная активная мощность источников изменяется в соответствии с активной мощностью нагрузки P_ΣГ = Р_ΣН, причём последняя следует за напряжением по статической характеристике Р_Н = f(U).

Рис. 3.15. Определение Uкр с помощью критерия устойчивости

Построенные характеристики имеют две точки пересечения (точки а и б на рис. 3.14). В этих точках баланса реактивных мощностей источников и нагрузки возможны установившиеся режимы. Однако только в точке а режим является устойчивым, режим в точке б – неустойчив, что легко обнаружить, создавая малые возмущения в режимах, соответствующих этим точкам.

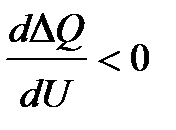
Если изобразить зависимость 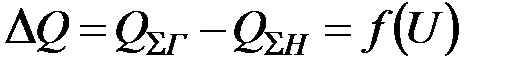, показанную на рис. 3.15, то можно видеть, что при устойчивом режиме работы 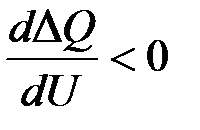, при неустойчивом .

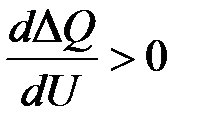Границей устойчивости будет равенство 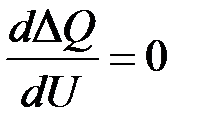, соответствующее критическому напряжению U_кр.

Теперь, зная аспекты статической устойчивости узла нагрузки, можно понимать, почему происходит явление «лавины напряжения» (рис. 3.16). При снижении напряжения в узле нагрузки до критического U_кр АД может опрокинуться, что вызывает повышенное потребление реактивной мощности. Вот почему важно поддерживать уровень напряжения в узлах энергосистемы в нормативном диапазоне.

 

Лавина напряжения

 

Рис. 3.16. Схема реализации лавины напряжения в энергосистеме

 

Контрольные вопросы

 

1. При каком соотношении мощности генератора и турбины система находится в устойчивом состоянии?

2. Запишите выражение критерия статической устойчивости.

3. Сформулируйте критерий статической устойчивости.

4. Запишите выражение запаса статической устойчивости.

5. Поясните термин «точка устойчивого равновесия».

6. Поясните термин «точка неустойчивого равновесия».

7. Каковы критерии устойчивости узла нагрузки?

8. Что понимается под термином «опрокидывание» двигателя?

ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ

ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ