Мы рассмотрели интерференционные опыты, в которых деление амплитуды световой волны от источника происходило в результате частичного отражения на поверхностях плоскопараллельной пластинки. Локализованные полосы при протяженном источнике можно наблюдать и в других условиях. Оказывается, что для достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Возникающие при этих условиях полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.
Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина).
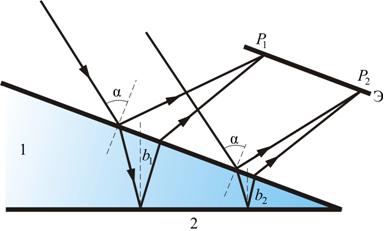
Рис. 8.10
Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают. Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость).
Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности.
Результат интерференции в точках 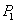 и
и 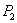 экрана определяется по известной формуле
экрана определяется по известной формуле 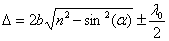 , подставляя в неё толщину пленки в месте падения луча (
, подставляя в неё толщину пленки в месте падения луча ( 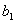 или
или 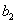 ). Свет обязательно должен быть параллельным (
). Свет обязательно должен быть параллельным ( 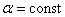 ): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет.
): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет.
Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис. 8.11). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
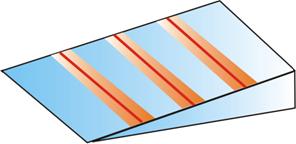
Рис. 8.11
3.8
Стоячая волна как частный случай интерференции. Уравнение плоской стоячей волны. Амплитуда стоячей волны. Узлы и пучности стоячей волны. Изменение вида стоячей волны со временем.
Превращения энергии в стоячей волне.
Образование стоячих волн в сплошных ограниченных средах. Условие их возникновения.
1)Стоя́чая волна́ — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует
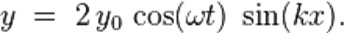
где:
· y0 — амплитуда волны,
·  — циклическая (угловая) частота, измеряемая в радианах в секунду,
— циклическая (угловая) частота, измеряемая в радианах в секунду,
· k — волновой вектор, измеряется в радианах на метр, и рассчитывается как 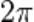 поделённое на длину волны
поделённое на длину волны  ,
,
· x и t — переменные для обозначения длины и времени.
Пучность — участок стоячей волны, в котором колебания имеют наибольшую амплитуду. Противоположностью пучности является узел — участок волны, в котором амплитуда колебаний минимальна.
Причиной пучности является сложение падающей и отраженной когерентных волн в «фазе», узел — сложение когерентных волн в «противофазе». При суперпозиции двух сигналов, близких по частоте и по амплитуде также образуются пучности и сужения.
2)Энергия в стоячей волне распределена так, что в областях, близких к узлам волны, сосредоточивается главным образом энергия потенциальная, а в областях, близких к пучностям волны, сосредоточивается энергия кинетическая. В тот момент времени, когда кинетическая энергия волны достигает максимума, потенциальная энергия становится минимальной. Через четверть периода максимума достигает энергия потенциальная, а энергия кинетическая убывает до нуля. Таким образом, в стоячей волне происходит непрерывное превращение и перераспределение энергии, но переноса энергии нет.
3)Собственные колебания таких систем связаны с образованием стоячих волн, особенности которых определяются условиями отражения на границах. Возбудить колебания в системе с распределёнными параметрами проще всего кратковременным воздействием, например ударом или щипком. Возникший волновой импульс «побежит» от места своего рождения во все доступные направления. В струне, к примеру, доступно одно лишь направление, по длине. Ввиду ограниченности области распространения колебаний, образовавшаяся волна, дойдя до границ колеблющегося тела, отразится и окажется, как бы «запертой» внутри ограниченного телом пространства. Прямые и отражённые волны, накладываясь, друг на друга, образуют стоячую волну. Параметры стоячей волны существенным образом зависят от условий отражения на границах. Стоячие волны не исчезают сразу после окончания возбуждения. Длительность существования стоячих вол зависит, прежде всего, от потерь, связанных с излучением энергии в окружающую среду и внутренним трением. Поскольку рассматриваемые колебания существуют после прекращения действия источника внешней силы, их относят к собственным колебаниям с затуханием.
3.9
Дифракция волн. Объяснение дифракции волн на основе принципа Гюйгенса – Френеля.
Дифракционная картина, наблюдаемая на плоском экране, если круглое отверстие освещается красным светом, и если между точечным источником красного света и экраном расположена круглая преграда.
1)Явление огибания волнами препятствий получило название дифракции. Для проявления дифракции размеры препятствий должны быть меньше или сравнимы с длиной волны.
Принцип Гюйгенса-Френеля
Каждый элемент поверхности, которой достигла в данный момент волна, является источником вторичных волн, распространяющихся в первоначальном направлении со скоростью исходной волны.
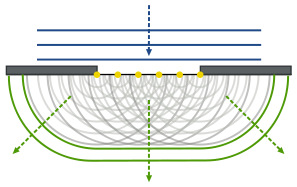
Все вторичные источники, расположенные на поверхности фронта волны, когерентны между собой. Согласно Френелю дифракция есть интерференция вторичных волн.
2) Сферическая волна, распространяющаяся из точечного источника S , встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259).
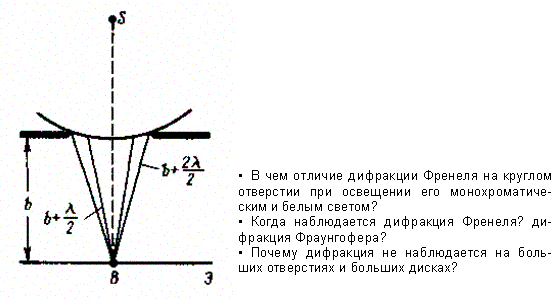
Рис. 259
Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),
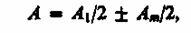
где знак плюс соответствует нечетным m и минус - четным m.
Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А =А1, т.е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием (см. § 177). Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если т нечетное - то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.
Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.
Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то Am ≪ A1 и результирующая амплитуда A = A1/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.
3.10
Дифракция Фраунгофера (дифракция в параллельных лучах), ее отличие от дифракции Френеля. Способы осуществления дифракции Фраунгофера.
Дифракция Фраунгофера от одной щели. Условия максимумов и минимумов дифракции. Распределение интенсивности света по экрану.
1)Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка 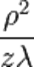 , что сильно упрощает теоретическое рассмотрение явления. Здесь
, что сильно упрощает теоретическое рассмотрение явления. Здесь  — расстояние от отверстия или преграды до плоскости наблюдения,
— расстояние от отверстия или преграды до плоскости наблюдения, 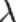 — длина волны излучения, а
— длина волны излучения, а 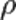 — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля
— радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля  , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.
, при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.
Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).
Дифракция Френеля :
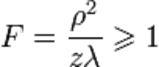
|
Дифракция Фраунгофера:
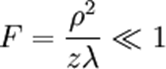
|
Дата: 2019-07-24, просмотров: 337.