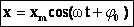
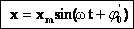
Скорость и ускорение точки, совершающей гармонические колебания.
Согласно определению скорости, скорость – это производная от координаты по времени
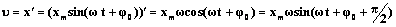
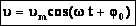
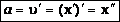Согласно определению ускорения, ускорение – это производная от скорости по времени:
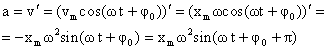- вторая производная от координаты по времени.
Тогда:
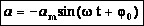
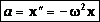
1.13.
Динамика гармонических колебаний; квазиупругая сила.
Второй закон Ньютона позволяет, в общем виде, записать связь между силой и ускорением, при прямолинейных гармонических колебаниях материальной точки (или тела) с массой m.
Т.к. исходя из второго закона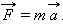 
, можно записать: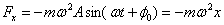 
Квазиупругая сила- сила, не являющаяся по своей природе упругой и подчиняющаяся закону F=-kx
Приведите примеры колебательных систем и укажите силы, выполняющие в них роль квазиупругой силы.
1.14.
Физический маятник.
Физический маятник - твёрдое тело способное совершать колебания относительно оси, не совпадающей с центром масс.
Используя основной закон динамики вращательного движения, покажите, что при малых углах отклонения он совершает гармонические колебания.
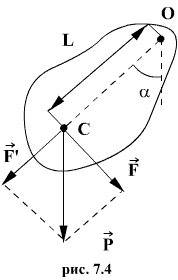
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
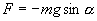
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
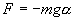
Для вывода закона движения физического маятникА используем основное уравнение динамики вращательного движения
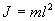. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
|
|
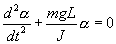
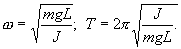
Решение этого уравнения
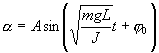
Приведенная длина и период колебаний физического маятника.
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.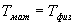 
или
.
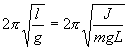Из этого соотношения определяем
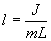
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
1.15.
Кинетическая, потенциальная и механическая энергии гармонически колеблющегося тела. Их формулы.
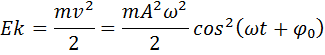
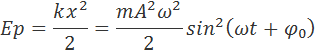
Величину полной механической энергии Е можно рассчитать как сумму величин кинетической и потенциальной энергий.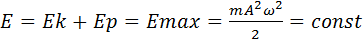 
2. Электричество и магнетизм
2.1.
Дата: 2019-07-24, просмотров: 215.
