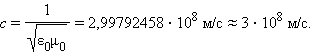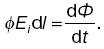1. Всякое перемещенное электрическое поле порождает вихревое магнитное поле. Переменное электрическое поле было названо Максвеллом, так как оно, подобно обычному току, вызывает магнитное поле. Вихревое магнитное поле порождается как токами проводимости Iпр (движущимися электрическими зарядами), так и токами смещения (перемещенным электрическим полем Е).
Первое уравнение Максвелла
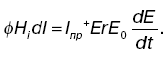2. Всякое перемещенное магнитное поле порождает вихревое электрическое (основной закон электромагнитной индукции).
Второе уравнение Максвелла :
Электромагнитное излучение.
Электромагни́тные во́лны, электромагни́тное излуче́ние — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.
3.1. Волна - это колебания, распространяющиеся в пространстве в течение времени.
Механические волны могут распространяться только в какой-нибудь среде (веществе): в газе, в жидкости, в твердом теле. Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды. Необходимым условием для появления упругих волн является возникновение в момент возмущения среды препятствующих ему сил, в частности, упругости. Они стремятся сблизить соседние частицы, когда они расходятся, и оттолкнуть их друг от друга в момент сближения. Силы упругости, действуя на удаленные от источника возмущения частицы, начинают выводить их из равновесия. Продольные волны характерны только газообразным и жидким средам, а вот поперечные – также и твердым телам: причина этого заключается в том, что частицы, составляющие данные среды, могут свободно перемещаться, так как жестко не зафиксированы, в отличие от твердых тел. Соответственно, поперечные колебания принципиально невозможны.
Продольные волны возникают тогда, когда частицы среды колеблются, ориентируясь вдоль вектора распространения возмущения. Поперечные волны распространяются в перпендикулярном вектору воздействия направлении. Короче: если в среде деформация, вызванная возмущением, проявляется в виде сдвига, растяжения и сжатия, то речь идет о твердом теле, для которого возможны как продольные, так и поперечные волны. Если же появление сдвига невозможно, то среда может быть любой.
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Поскольку скорость волны - величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
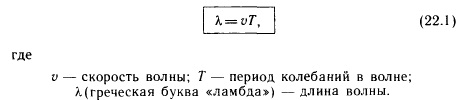
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду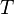 
колебаний, поэтому
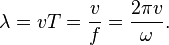
Волновое число (также называемое пространственной частотой) — это отношение 2π радиан к длине волны: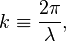 
пространственный аналог круговой частоты.
Определение: волновым числом k называется быстрота роста фазы волны φ по пространственной координате.
3.2. Плоская волна — волна, фронт которой имеет форму плоскости.
Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту. Плоская волна является частным решением волнового уравнения и удобной моделью: такая волна в природе не существует, так как фронт плоской волны начинается в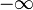 
и заканчивается в 
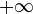, чего, очевидно, быть не может.
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции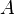 
записывается в виде:
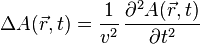где
· 
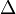- оператор Лапласа;
· 
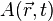— искомая функция;
· 
— радиус вектора искомой точки;
· 
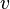— скорость волны;
· 
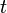— время.
Волновая поверхность — геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Частный случай волновой поверхности — волновой фронт.
А) Плоская волна – это волна, волновые поверхности которой представляют собой совокупность параллельных друг другу плоскостей. 
Б) Сферическая волна – это волна, волновые поверхности которой представляют собой совокупность концентрических сфер.
Луч — линия, нормальной и волновой поверхности. Под направлением распространения волн понимают направление лучей. Если среда распространения волны однородная и изотропная, лучи прямые (причём, если волна плоская — параллельные прямые).
Понятием луч в физике обычно пользуются только в геометрической оптике и акустике, так как при проявлении эффектов, не изучаемых в данных направлениях, смысл понятия луч теряется.
3.3. Энергетические характеристики волны
Среда, в которой распространяется волна, обладает механической энергией, складывающейся из энергий колебательного движения всех ее частиц. Энергия одной частицы с массой m0 находится по формуле: Е0 = m0 Α2ω2/2. В единице объема среды содержится n = p/m0 частиц (ρ - плотность среды). Поэтому единица объема среды обладает энергией wр = nЕ0 = ρΑ2ω2/2.
Объемная плотность энергии (Wр) - энергия колебательного движения частиц среды, содержащихся в единице ее объема: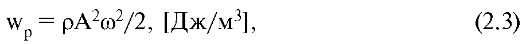 
Поток энергии (Ф) - величина, равная энергии, переносимой волной через данную поверхность за единицу времени: 
Интенсивность волны или плотность потока энергии (I) - величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны: 
3.4. Электромагнитная волна
Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.
Условие возникновения электромагнитных волн. Изменения магнитного поля происходят при изменении силы тока в проводнике, а сила тока в проводнике изменяется при изменении скорости движения электрических зарядов в нем, т. е. при движении зарядов с ускорением. Следовательно, электромагнитные волны должны возникать при ускоренном движении электрических зарядов. При скорости заряда, равной нулю, существует только электрическое поле. При постоянной скорости заряда возникает электромагнитное поле. При ускоренном движении заряда происходит излучение электромагнитной волны, которая распространяется в пространстве с конечной скоростью.
Электромагнитные волны распространяются в веществе с конечной скоростью.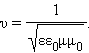 
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
| |
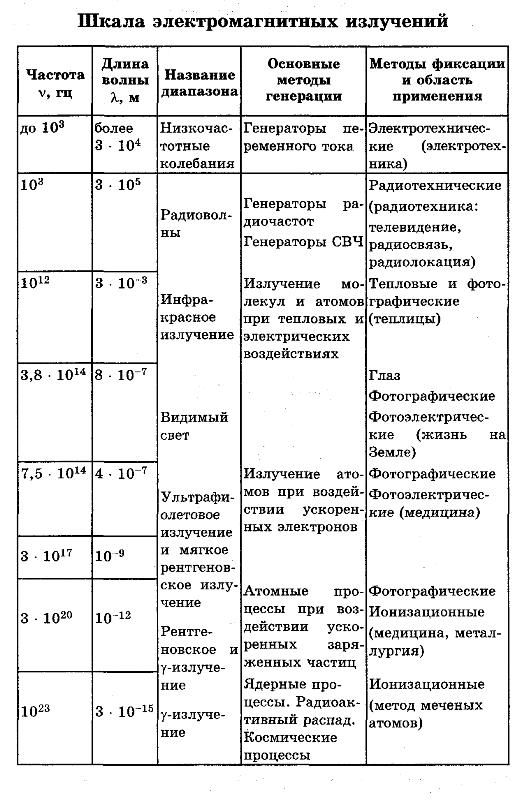
| Шкала электромагнитных волн: |
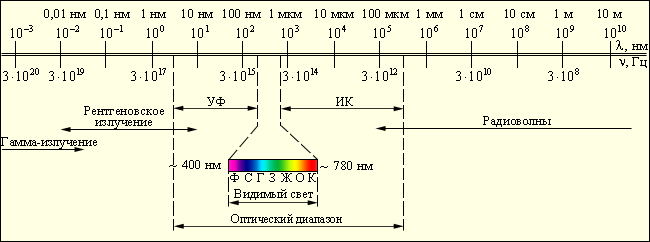
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше.
Электромагнитное излучение принято делить по частотам диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
3.6
Интерференция волн. Когерентные волны. Условия когерентности волн.
Оптическая длина пути (о.д.п.) света. Связь разности о.д.п. волн с разностью фаз колебаний, вызываемых волнами.
Амплитуда результирующего колебания при интерференции двух волн. Условия максимумов и минимумов амплитуды при интерференции двух волн.
Интерференционные полосы и интерференционная картина на плоском экране при освещении двух узких длинных параллельных щелей: а) красным светом, б) белым светом.
1) ИНТЕРФЕРЕНЦИЯ ВОЛН - такое наложение волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн.
Необходимые условия для наблюдения интерференции:
1) волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени (или менялась не очень быстро, что бы её можно было успеть зарегистрировать);
2) волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции (попробуйте сложить две перпендикулярные синусоиды!). Иными словами, складываемые волны должны иметь одинаковые волновые векторы (или близконаправленные).
Волны, для которых выполняются эти два условия, называются КОГЕРЕНТНЫМИ. Первое условие иногда называют временной когерентностью, второе - пространственной когерентностью.
Дальше пример.
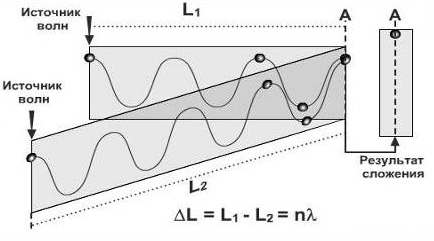
Рассмотрим в качестве примера результат сложения двух одинаковых однонаправленных синусоид. Варьировать будем только их относительный сдвиг. Иными словами, мы складываем две когерентные волны, которые отличаются только начальными фазами (либо их источники сдвинуты друг относительно друга, либо то и другое вместе).
Если синусоиды расположены так, что их максимумы (и минимумы) совпадают в пространстве, произойдет их взаимное усиление.
Если же синусоиды сдвинуты друг относительно друга на полпериода, максимумы одной придутся на минимумы другой; синусоиды уничтожат друг друга, то есть произойдет их взаимное ослабление.
Математически это выглядит так. Складываем две волны:
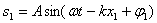
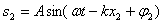
здесь х1 и х2 - расстояния от источников волн до точки пространства, в которой мы наблюдаем результат наложения. Квадрат амплитуды результирующей волны (пропорциональный интенсивности волны) дается выражением:
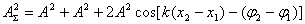
Максимум этого выражения есть 4 A 2, минимум - 0; всё зависит от разности начальных фаз и от так называемой разности хода волн :
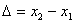
При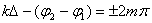 
в данной точке пространства будет наблюдаться интерференционный максимум, при 
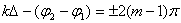- интерференционный минимум.
В нашем простом примере источники волн и точка пространства, где мы наблюдаем интерференцию, находятся на одной прямой; вдоль этой прямой интерференционная картина для всех точек одинакова. Если же мы сдвинем точку наблюдения в сторону от прямой, соединяющей источники, мы попадем в область пространства, где интерференционная картина меняется от точки к точке. В этом случае мы будем наблюдать интерференцию волн с равными частотами и близкими волновыми векторами.
2)1. Оптической длиной пути называется произведение геометрической длины d пути световой волны в данной среде на абсолютный показатель преломления этой среды n.
s=nd.
2. Разность фаз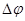 
двух когерентных волн от одного источника, одна из которых проходит длину пути 
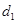в среде с абсолютным показателем преломления 
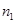, а другая – длину пути 
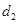в среде с абсолютным показателем преломления 
:
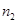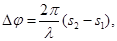
где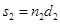 
, 
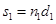, λ – длина волны света в вакууме.
3)Амплитуда результирующего колебания зависит от величины, называемой разностью хода волн.
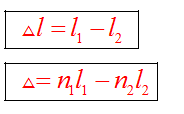
Если разность хода равна целому числу волн, то волны приходят в точку синфазно. Складываясь, волны усиливают друг друга и дают колебание с удвоенной амплитудой.
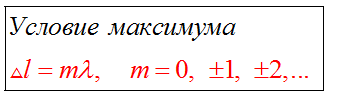
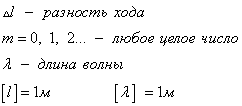
Если разность хода равна нечетному числу полуволн, то волны приходят в точку А в противофазе. В этом случае они гасят друг друга, амплитуда результирующего колебания равна нулю.
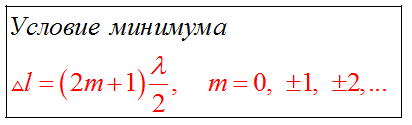
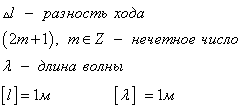
В других точках пространства наблюдается частичное усиление или ослабление результирующей волны.
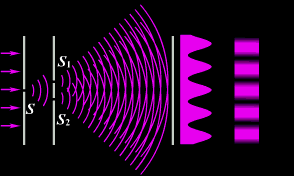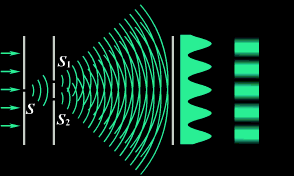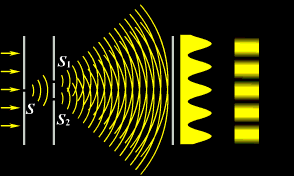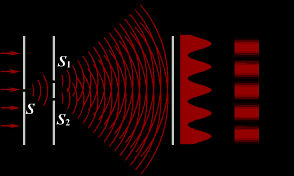
4)Опыт Юнга
В 1802 г. английский ученый Томас Юнг поставил опыт, в котором наблюдал интерференцию света. Свет из узкой щели S, падал на экран с двумя близко расположенными щелями S1 и S2. Проходя через каждую из щелей, световой пучок расширялся, и на белом экране световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
3.7
Осуществление интерференции света от обычных источников света.
Интерференция света на тонкой пленке. Условия максимумов и минимумов интерференции света на пленке в отраженном и в проходящем свете.
Интерференционные полосы равной толщины и интерференционные полосы равного наклона.
1)Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.
2) 
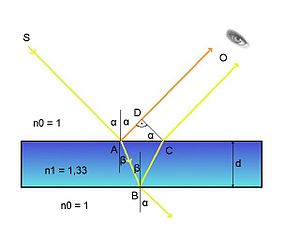интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённыхобъективов. Луч света, проходя через плёнку толщиной 
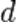, отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при 
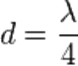, где 
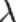— длина волны. Если 
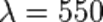нм, то толщина плёнки равняется 550:4=137,5 нм.
Лучи соседних участков спектра по обе стороны от 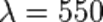нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей
— условие максимума;
— условие минимума,
где k=0,1,2… и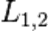 
— оптическая длина пути первого и второго луча, соответственно.
3)Полосы равного наклона
Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 8.8).
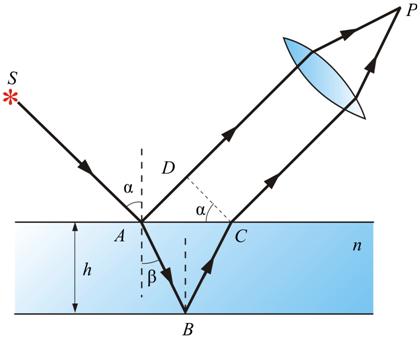
Рис. 8.8
В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точкеP такая же, как на линии DC:
.
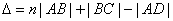Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е.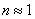 
. Так как 
, 
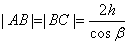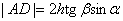(h – толщина пластинк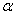и, 
и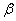 
– углы падения и преломления на верхней грани; 
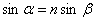), то для разности хода получаем
.
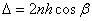Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:
,
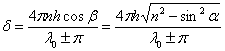где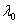 
– длина волны в вакууме.
В соответствии с последней формулой светлые полосы расположены в местах, для которых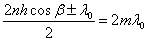 
, где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.
Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.
Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис. 8.9). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало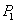 
посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя 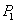, дает 
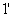, а луч 2, отражаясь от з2 и далее от 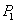, дает 
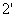. Пластинк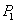и и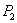 
одинаковы по размерам. 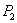ставится для компенсации разности хода второго луча. Луч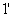и и 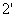когерентны и интерферируют.
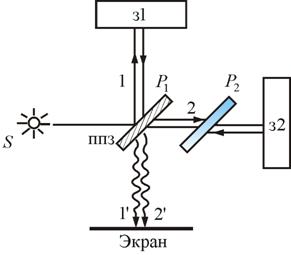
Рис. 8.9
Дата: 2019-07-24, просмотров: 681.
