Диск или цилиндр вращающийся вокруг центральной оси
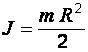
Момент инерции стержня при вращении относительно оси, проходящей через его конец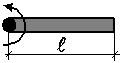
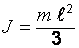
Момент инерции стержня при вращении относительно оси, проходящей через его центр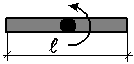
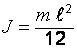
Момент инерции шара при вращении относительно оси, проходящей через его центр

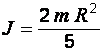
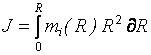Момент инерции тела, если известно распределение массы тела относительно оси вращения m_i (R), может быть определён как

Теорема Штейнера.

Момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

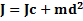
Jc— известный момент инерции относительно оси, проходящей через центр масс тела,

J — искомый момент инерции относительно параллельной оси,

m— масса тела,

d— расстояние между указанными осями.

Основной закон динамики вращательного движения.

       Изменение момента количества движения твердого тела 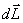, равно импульсу момента 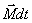всех внешних сил, действующих на это тело.

Согласно( 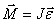 )второй закон Ньютона для вращательного движения 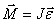По определению угловое ускорение 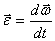и тогда это уравнение можно переписать следующим образом:

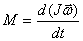
с учетом ( ):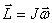

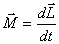
или

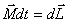
1.8.

Момент импульса тела относительно оси.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что 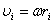, получим

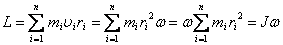
Выражение основного закона динамики вращательного движения через изменение момента импульса тела.

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей Li, взятых относительно одной и той же точки выбранной системы отсчета.

L = ΣLi.

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.

dL/dt = M.

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.

Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением

.

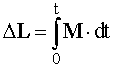Закон сохранения момента импульса. Примеры.

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):
.

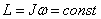Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы (рис. 6.9).

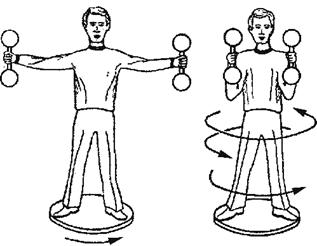 Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского (рис. 6.11).

1.9.

Работа силы.

Работа силы - мера действия силы при превращении механического движения в другую форму движения.

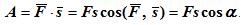
Примеры формул работы сил.

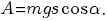
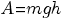работа силы тяжести;            работа силы тяжести наклонной пов-ти

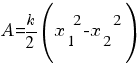
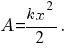работа силы упругости

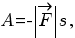работа силы трения