Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки Vi=VC
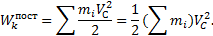
или
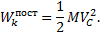
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.
Вращательное движение . Если тело вращается вокруг какой-нибудь оси О z , то скорость любой его точки 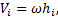 где
где 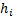 - расстояние точки от оси вращения, а
- расстояние точки от оси вращения, а 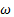 - угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:
- угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:
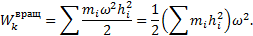
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z . Таким образом, окончательно найдем:
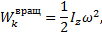
1.11.
Механическая энергия тела.
Механическая энергия — это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу.
Закон сохранения механической энергии.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
|
Связь работы неконсервативных сил с изменением механической энергии системы тел.
Если несколько тел взаимодействуют между собой только Fтяж и Fупруг, и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготяния равна изменению потенциальной энергии. Взаимодействие с протиположным знаком
| A = - (Ep2 - Ep1) | (1)
Вместве с тем по теореме о кинетичской энергии работа тех же сил равна изменнеию кинитической энергии
| A = - (Eк2 - Eк1) | (2)
Из сравнения равенств (1) и (2) видно, что изменение кинитической энергии тел в замкнутой системе равно по абсолютному значению измению потенциала энергии системы тел и противоположно ему по знаку
Eк2 - Eк1 = - (Ep2 - Ep1) (3)
Из равенства (3) следует, что сумма Ek и Ep остоётся постоянной.
A = ∆E, где A работа непотенциальных сил.
1.12.
Кинематика колебательного движения: смещение, амплитуда, фаза, циклическая частота.
Колебательные движения –– это движения, повторяющиеся во времени. Простейшей периодической функцией является гармоническая функция cos или sin.
Характеристика колебаний
Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.
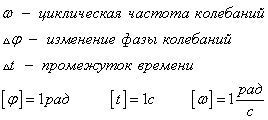 Циклическая частота характеризует скорость изменения фазы колебаний.
Циклическая частота характеризует скорость изменения фазы колебаний.
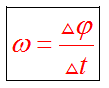
Начальное состояние колебательной системы характеризует начальная фаза 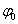
Амплитуда колебаний A - это наибольшее смещение из положения равновесия
Период T - это промежуток времени, в течение которого точка выполняет одно полное колебание.
Частота колебаний - это число полных колебаний в единицу времени t.
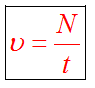

Частота, циклическая частота и период колебаний соотносятся как
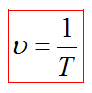
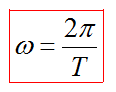
Дата: 2019-07-24, просмотров: 351.