В последние годы появились эксперименты [1-3, 4-9], в которых исследуются оптические свойства систем, представляющих диэлектрическую матрицу с вкрапленными в нее частицами полупроводника. Технология этих систем такова, что полупроводниковые частички с достаточно хорошей точностью можно считать шарообразными, причем дисперсия их радиусов сравнительно невелика. Очень важно, что технология позволяет получать системы, в которых средний радиус полупроводниковых частиц меняется практически непрерывно. Поэтому исследования оптических свойств этих систем в зависимости от радиуса шаров представляет мощный метод изучения параметров полупроводников, в значительной мере аналогичный магнитооптическому.

В полупроводниковом шаре возникает размерное квантование электронных и дырочных состояний, приводящих к тому, что оптические линии смещаются в зависимости от радиуса шара [1-3]. Авторы предлагают здесь теоретическое описание этого явления в рамках простейшей модели, использующей стандартную зонную схему.

Предполагалось, что зоны электронов и дырок имеют параболическую форму с массами m_e и m_h соответственно, причем m_e<<m_h. Тогда характер размерного квантования определяется соотношением трех длин: a , a_e , a_h , где a_e > a_h ; а – радиус шара, a_e , a_h – боровские радиусы электронов и дырок, соответственно, в полупроводнике с диэлектрической проницаемостью e. Предполагаемая теория построена в приближении метода эффективной массы, т.е. в предположении, что существенные длины велики по сравнению с постоянной решетки. Волновая функция электронов и дырок будет считаться равной нулю на поверхности шара, что соответствует бесконечно высокой потенциальной стенке.

Рассмотрим случай сильного размерного квантования, когда a >> a_h. Расстояние между уровнями размерного квантования для электронов и дырок порядка ħ²/( m_e · a ² ) и ħ²/( m_h · a ² ).

При межзонном поглощении должна наблюдаться серия дискретных линий. Порогом поглощения является величина

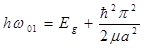             (1.1),

где 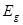- ширина запрещенной зоны; 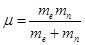- приведенная масса.

Учет дисперсии шаров по размерам приводит к замене выражения для порога поглощения (1.1) на следующее:

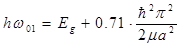      (1.2).

Отсюда виден закон, по которому эффективная ширина запрещенной зоны увеличивается с уменьшение радиуса шара а, прочие линии сдвигаются в коротковолновую сторону по закону

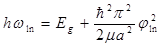          (1.3),

где 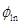 - корни функции Бесселя.

Если ширина линий сравнима с расстоянием между ними, то размерное квантование должно проявляться апериодическими осцилляциями поглощения, причем максимумы осцилляций должны сдвигаться в коротковолновую сторону по закону 1/а².