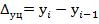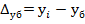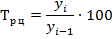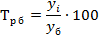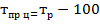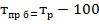Цель занятия – изучение методов расчета макроэкономических показателей на основе СНС.
Содержание занятия – заполнение основных счетов СНС и расчет макроэкономических показателей: ВВП, ВНД, ВНРД, прибыли экономики, чистых кредитов (чистых долгов), валового накопления, статистического расхождения.
Методические указания– при подготовке к занятию следует освоить основные категории СНС – рыночный и нерыночный выпуск, экономическая территория страны, резиденты, конечное и промежуточное потребление, сектор, институциональная единица.
Студент должен знать перечень основных счетов, заполняемых в российской версии СНС для экономики в целом, освоить связь между показателями отдельных счетов, изучить, какие макроэкономические показатели рассчитываются в каждом счете. Необходимо обратить внимание на то, какие счета балансируются по определению, а в каких используются дополнительные балансирующие показатели.
Обязательно знание трех методов расчета ВВП – производственного, распределительного и метода конечного использования, причем на основе актуальных статистических категорий.
Расчеты на основе СНС сопровождаются постоянно вносимыми корректировками в области классификационных групп и статистических категорий, поэтому следует обращаться к реальным статистическим расчетам, публикуемым на сайте Росстата, режим доступа: http://www.gks.ru
Основные теоретические подходы к расчету данных показателей следует изучить в данном пособии и в пособии [5],стр.185 –202.
Литература: [5], [6], [11], [13].
Интернет – ресурсы: [2], [6].
4 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
4.1 Общие указания по выполнению и оформлению контрольной работы
Вариант контрольного задания выдается преподавателем и зависит от порядкового номера студента в зачетной ведомости.
Контрольная работа состоит из двух частей: теоретической и практической. В теоретической части следует подробно рассмотреть два вопроса. Для выполнения данного раздела следует воспользоваться учебниками и учебными пособиями, перечень которых приводится в списке рекомендуемой литературы. В качестве дополнительного источника информации можно привлекать Интернет-ресурсы. Копирование ответов из данного учебного пособия и учебных пособий [4] и [5] НЕДОПУСТИМО.
В практической части требуется решить несколько задач. При решении задачи следует приводить ее условие, подробно расписать формулы, которые будут использованы при выполнении задания, полностью приводить все цифровые подстановки. После решения необходимо формулировать выводы. Без выводов задача считается выполненной не полностью.
Для решения задач рекомендуется предварительно изучить методики соответствующих расчетов, приводимые ниже, а также следует использовать материалы практикумов, представленных в списке рекомендуемой литературы под номерами: [3], [4], [7], [15].
Оформить работу можно в компьютерном варианте или рукописном виде. Возможно сочетание двух вариантов оформления: текст – в машинописном виде, формулы и решения задач – в рукописном варианте. При оформлении работы следует руководствоваться рекомендациями, изложенными в пособии [6] из списка рекомендуемой литературы.
Работа представляется для проверки на кафедру в установленные учебным графиком сроки, но не позднее даты проведения экзамена. После проверки работа допускается к защите или отправляется на доработку.
Если работа допускается к защите, студент должен ее защитить, т.е. должен быть готов ответить на все вопросы по теоретическому разделу или методике решения задачи. После защиты контрольной работы студент получает допуск к экзамену.
Если работа отправляется на доработку, следует устранить все замечания, изложенные преподавателем, и повторно сдать ее на проверку.
Примеры решения задач по теме «Абсолютные и относительные величины»
Перед решением задач, относящихся к данной теме, следует изучить методики расчета каждого вида относительных показателей, приведенные на стр. 14-17 данного пособия. Ниже приведены примеры расчета каждого вида относительных показателей.
Пример 1 - Расчет относительных показателей планового задания, выполнения плана и динамики
Численность сотрудников предприятия по состоянию на 31.12.2015 составляла 12560 чел. Планировалось, к концу 2016увеличить количество сотрудников до 12800 чел. Фактическая численность сотрудников по состоянию на 31.12.2016 составила 12730 чел.
Определите относительные показатели планового задания, выполнения плана и динамики.
Решение:
Определим относительный показатель планового задания, используя формулу (4.1):
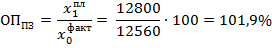
Следовательно, планировалось увеличение численности сотрудников на 1,9%.
Степень выполнения планового задания определим по формуле (4.2):
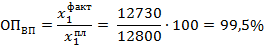
Результат расчетов показывает, что планируемая численность не была достигнута, план по численности сотрудников не довыполнен на 0,5% (99,5% - 100% = - 0,5%).
Однако, динамика показателя положительная, количество сотрудников за год возросло на 1,4%, что подтверждает расчет относительной величины динамики на основе формулы (4.3):
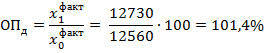
Пример 2 - Расчет относительных показателей структуры и координации
Численность городского населения в РФ в 2016 составляла 108,6 млн. чел., а численность сельского населения – 37,9 млн. чел.[1]
Определить структуру населения и соотношение городского и сельского населения.
В качестве показателя структуры рассчитаем доли городского и сельского населения, используя формулу (4.3). Доля горожан составит:
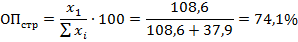
где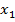 
– численность городского населения;
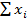– общая численность населения РФ.
Доля сельских жителей будет рассчитываться аналогично:
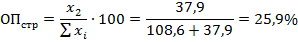
где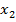 
- численность сельского населения.
Для характеристики соотношения городского и сельского населения используем относительные показатели координации (формула 4.5):
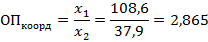
В этом случае можно говорить о том, что на одного сельского жителя в РФ в 2016 году приходилось 2,865 горожанина, но лучше умножить результат на 1000, и тогда мы будем говорить, что на 1000 селян приходилось 2865 горожан.
При использовании второго способа расчета получим следующие результаты:
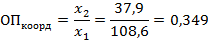
Таким образом, получаем, что на одного горожанина в РФ в 2016 году приходилось 0,349 сельских жителей. Используя умножение до целых чисел, получаем, что на 1000горожан приходилось 349жителей сел.
Пример 3 - Расчет относительных показателей интенсивности
На сайте Росстата приводится информация о количестве зарегистрированных браков. В 2016 году в РФ было зарегистрировано 1 161 068 браков. Средняя численность населения в этом году составляла 146,5 млн. чел.[2]
В качестве относительного показателя интенсивности брачного процесса используем коэффициент брачности (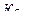 
), который рассчитывается по формуле как отношение количества зарегистрированных браков к средней численности населения, умноженное на 1000.
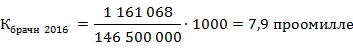
Следовательно, на 1 тыс. человек населения РФ в 2016 приходилось 7,9 брака.
Пример 4 - Расчет относительных показателей сравнения
Сравним показатели прожиточного минимума в РФ для разных демографических групп в III квартале 2016 г. Известно, что прожиточный минимум пенсионеров в этот период составлял 8136 руб., трудоспособного населения - 10678 руб.[3]
Относительный показатель сравнения можно рассчитать двумя способами.
1 способ: разделим величину прожиточного минимума пенсионеров на величину прожиточного минимума трудоспособного населения:
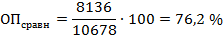
Следовательно, прожиточный минимум пенсионера составляет 76,2% от прожиточного минимума трудоспособного человека.
2 способ: разделим величину прожиточного минимума трудоспособного населения на величину прожиточного минимума пенсионеров:
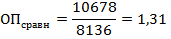
В этом случае мы можем констатировать, что прожиточный минимум трудоспособного в 1,32 раза выше прожиточного минимума пенсионера.
Примеры решения задач по теме « Средние величины и показатели вариации»
Виды средних величин и показателей вариации, а также формулы их расчета с пояснением принципов выбора вида и формы показателя приведены на стр. 18-23 данного пособия.
Пример 5 - Расчет средней величины в интервальных рядах распределения
В таблице 7 приведены условные данные о распределении предприятий по объему продаж:
Таблица 7 - Условные данные о распределения предприятий по объему продаж
| Объем продаж, тыс. руб. | Количество предприятий, шт. |
| до 100 | 2 |
| 100-140 | 15 |
| 140-180 | 10 |
| свыше 180 | 4 |
Определите средний объем продаж в расчете на одно предприятие.
Решение:
При расчете среднего значения признака в интервальных вариационных рядах используется средняя арифметическая взвешенная, определяемая по формуле (5.2), приведенной в таблице 3:
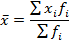
В формуле в качестве значения признака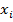 
используется дискретное число, однако в приведенном примере значение признака приводится в виде интервала. В этом случае за 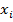принимается середина каждого интервала, определяемая как полусумма максимального и минимального значения признака в группе.
Например, если группировочный интервал 8-10, за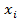 
будет принято число 9, так как полусумма максимального и минимального значения признака в группе будет определена следующим образом:
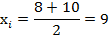
При наличии открытых интервалов, у которых определена только одна граница – верхняя или нижняя, открытый интервал принимается равным по величине смежному с ним закрытому интервалу.
У первой группы имеется открытый интервал, в котором указана только верхняя граница. В нашем случае, он принимается равным по величине второму интервалу, т. е. считается, что у первой группы объем продаж составит от 60 до 100 тыс. руб. Серединой интервала в данном случае будет объем продаж, равный 80 тыс. руб. (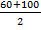 
).
Открытый интервал у последней группы принимается равным по величине предшествующему интервалу, т. е. примет значения от 180 до 220 тыс. руб., а середина интервала будет рассчитана (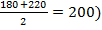 
)
Средний объем продаж по данной совокупности определим так:
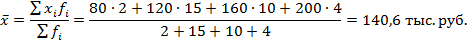
Пример 6 - Расчет средней, показателей вариации, моды и медианы в интервальном вариационном ряду распределения
Имеются данные о затратах времени на изготовление деталей в 200 отраслях:
Таблица 8 -Условные данные о затратах времени на изготовление деталей
| Время, затраченное на изготовление 1 детали, мин. | Число деталей, штук | Сумма накопленных частот, Si |
| 1 | 2 | 3 |
| 8-10 | 14 | 14 |
| 10-12 | 26 | 40 |
| 12-14 | 75 | 115 |
| 14-16 | 40 | 155 |
| 16-18 | 20 | 175 |
| 18-20 | 15 | 190 |
| 20-22 | 10 | 200 |
| Итого | 200 | Х |
По приведенным данным вычислите:
1. Среднее значение варьирующего признака;
2. Показатели вариации: размах, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициенты вариации и осцилляции;
3. Моду и медиану.
Решение:
Задачи данного типа рекомендуется решать в табличной форме. За значение признака ( 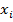) принимаются середины интервалов, методика определения которых рассмотрена в предыдущем примере.
Определим среднее значение признака по формуле средней арифметической взвешенной (5.2), подставляя данные из гр. 3 и 2 таблицы 9:
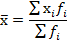
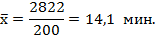
Таблица 9 - Расчетная таблица
| xi | fi | xifi |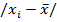 
| 
|  
|
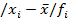
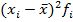
| 1 | 2 | 3 | 4 | 5 | 6 |
| 9 | 14 | 9 · 14 = 126 | |9 - 14,1| = 5,1 | 5,1 · 14 = 71,4 | 5,12 · 14 = 364,14 |
| 11 | 26 | 11 · 26 = 286 | |11 - 14,1| = 3,1 | 3,1 · 26 = 80,6 | 3,12 · 26 = 249,86 |
| 13 | 75 | 975 | 1,1 | 82,5 | 90,75 |
| 15 | 40 | 600 | 0,9 | 36,0 | 32,40 |
| 17 | 20 | 340 | 2,9 | 58,0 | 168,20 |
| 19 | 15 | 285 | 4,9 | 73,5 | 360,15 |
| 21 | 10 | 210 | 6,9 | 69,0 | 476,10 |
| Итого | 200 | 2822 | 24,9 | 471,0 | 1741,60 |
Размах вариации рассчитываем как разницу между серединами первого и последнего интервалов:
R = 21 - 9 = 12 мин.
Среднее линейное отклонение определяется по формуле (5.14):
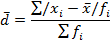
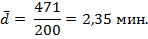
Среднее квадратичное отклонение определим по формуле (5.16):
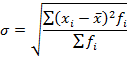
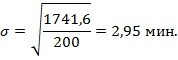
данные для расчета дисперсии содержатся в графах 2 и 6 таблицы 9. В данном примере она определяется по формуле (5.18):
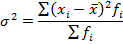
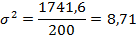
коэффициент вариации определяем, подставляя данные в формулу (5.22):
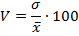
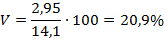
Коэффициент осцилляции в нашем примере определяется по формуле (5.20) и он равен:
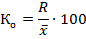
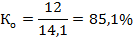
2. Чтобы определить моду в данном интервальном ряду распределения, воспользуемся формулами (5.10):
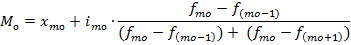
Вначале определяют модальный интервал, т.е. интервал, имеющий наибольшую частоту. В данном примере модальным является интервал 12-14 минут, т.к. его частота составляет 75 единиц.
Нижняя граница модального интервала (хмо) составит 12, величина модального интервала (iмо) = 2, частота модального интервала (fмо) = 75, частота интервала, предшествующего модальному (f(мо-1)) = 26, частота интервала, следующего за модальным (f(мо+1)) = 40. Следовательно, мода равна:
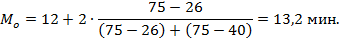
Для определения медианы в интервальном ряду распределения воспользуемся формулой (5.11):
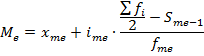
Найдем медианный интервал. У медианного интервала сумма накопленных частот должна быть равна половине суммы всех частот ряда или превышать эту величину. В нашем примере сумма всех частот равна 200 единицам, полусумма - 100 единиц (200 : 2).
В гр. 3 таблицы 8 рассчитываются суммы накопленных частот последовательным сложением частот каждой группы. Для первой группы сумма накопленных частот - 14 единиц, для второй - 40 (14+26), для третьей - 115 (14 + 26 + 75) и т.д.
В третьей группе сумма накопленных частот впервые превысит полусумму всех частот ряда (115 больше 100), следовательно, третья группа является медианной, а медианный интервал - 12-14 мин. тогда медиана равна:
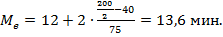
Вывод. из приведенных расчетов видно, что среднее время на изготовление 1 детали составит 14,1 мин., при этом половина рабочих затратит на изготовление 1 детали в среднем не более 13,6 мин. (Ме = 13,6), а самая многочисленная группа затратит на изготовление 1 детали в среднем 13,2 мин.
Индивидуальное время на изготовление 1 детали отклоняется от среднего времени в среднем на 2,9 мин. (σ = 2,95), что составляет 20,9% (V = 20,9). Средняя типична для совокупности, т.к. коэффициент вариации не превышает 30%.
Примеры решения задач по теме « Анализ рядов динамики»
Показатели, характеризующие ряды динамики, формулы их расчета, а также принципы выбора соответствующих формул рассмотрены на стр. 25-30 данного пособия.
Пример 7 - Расчет показателей динамики
По данным таблицы 10 проанализировать динамику явления, рассчитав следующие показатели:
1. Цепные и базисные абсолютные приросты, темпы роста и темпы прироста;
2. Средний уровень ряда, средние темпы роста и темпы прироста, средние абсолютные приросты.
Таблица 10 - Данные о розничном товарообороте региона в 2016 г.
| Показатели | I кв. | II кв. | III кв. | IV кв. |
| Розничный товарооборот, млрд. руб. | 220,2 | 219,6 | 268,0 | 357,4 |
Решение:
Рассчитаем аналитические показатели динамики:
1. Абсолютный прирост (сокращение) определим по формулам (7.1) и (7.2):
| Цепной
| Δу1 = 219,6 - 220,2 = -0,6 млрд. руб. |
| Δу2 = 268,0 - 219,6 = 48,4 млрд. руб. | |
| Δу3 = 357,4 - 268,0 = 89,4 млрд. руб. | |
| Базисный
| Δу1 = 219,6 - 220,2 = -0,6 млрд. руб. |
| Δу2 = 268,0 - 220,2 = 47,8 млрд. руб. | |
| Δу3 = 357,4 - 220,2 = 137,4 млрд. руб. |
2. Темп роста определим по формулам (7.3) и (7.4):
| Цепной
| 
|
| |
| |
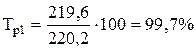
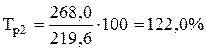
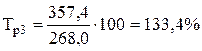
| Базисный
|
|
| |
 .
|
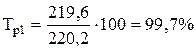
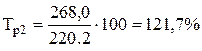
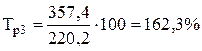3. Темп прироста находим по формуле (7.9):
| Цепной
| Тпр1 = 99,7 - 100,0 = -0,3% |
| Тпр2 = 122,0 - 100,0 = 22,0% | |
| Тпр3 = 133,4 - 100,0 = 33,4% | |
| Базисный
| Тпр1 = 99,7 - 100,0 = -0,3% |
| Тпр2 = 121,7 - 100,0 = 21,7% | |
| Тпр3 = 162,3 - 100,0 = 62,3%. |
4. Средний уровень ряда динамики определим по формуле средней арифметической простой, т.к. это интервальный ряд динамики.
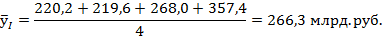
5. Средний абсолютный прирост определим по формуле (7.15):
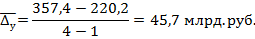
6. Средний темп роста можно рассчитать как по формуле (7.16), так и (7.17), так как ряд динамики полный. Используем оба способа расчета.
По формуле (7.16) средний темп роста равен:
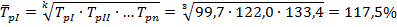
Формула (7.17) приводит к аналогичному результату:
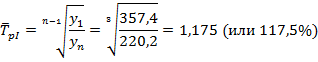
7. Средний темп прироста определим по формуле:
%
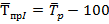
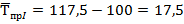На основе произведенных расчетов можно сделать следующие выводы:
1. Розничный товарооборот во II квартале 2016 г. по сравнению с I кварталом сократился на 0,6 млрд. руб. (0,3%), в III квартале по сравнению со II-м - увеличился на 48,4 млрд. руб. (22%), а в IV квартале по сравнению с III-м - возрос на 89,4 млрд. руб. (33,4%).
2. В целом за 2016 год товарооборот увеличился на 137,4 млрд. руб., или 62,3%. В среднем товарооборот составлял 266,3 млрд. руб. ежеквартально и увеличивался в среднем на 45,7 млрд. руб. (17,5%) в каждом квартале.
Пример 8 – Прогнозирование на основе метода экстраполяции
Выручка от продаж условного предприятия за 2012-2016 год возросла на 17,9 %, достигнув в 2016 году 345,0 млн. руб. Определите прогнозное значение выручки от продаж в 2018 году с учетом того, что тенденция изменения данного показателя сохранится.
Решение:
Согласно условию задачи, следует определить прогнозное значение объема продаж. В этом случае следует воспользоваться методом экстраполяции. Прогноз может осуществляться одним из двух способов:
• если наблюдается равномерный характер развития явления - на основе формулы (7.20):
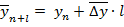
• если наблюдается равноускоренный характер развития явления - на основе формулы (7.21):
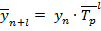
В нашем примере отсутствуют данные об абсолютных значениях показателей за каждый год, нет информации о цепных показателях динамики, имеется только информация об общем за весь период темпе прироста. Следовательно, мы сможем использовать только формулу (7.21), определив средний годовой темп роста по формуле (7.17):
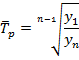
где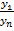 
–последний базисный темп роста, определяемый как отношение показателя в последнем периоде к значению показателя в первом периоде.
Абсолютные значения показателей отсутствуют, однако в условии указано, что выручка от продаж возросла на 17,9%, следовательно, речь идет о последнем базисном темпе прироста. На его основе определим последний базисный темп роста, исходя из формулы:
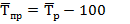
Тогда базисный последний темп роста составит:
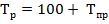
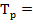100+17,9 = 117,9% или 1,179
Подставляя найденное значение в формулу (7.17), получим средний темп роста:
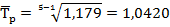
Тогда, прогнозное значение показателя в 2018 году, т.е. через два года, определим следующим образом, основываясь на формуле (7.21):
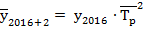
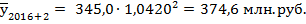
Следовательно, при сохранении существующих тенденций, выручка от продаж в 2018 году может составить 374,6 млн. руб.
Примеры решения задач по теме « Индексный анализ и его использование при анализе цен и инфляции»
Теоретические основы индексного анализа, формулы различных видов индексов и правила их построения рассмотрены на стр. 31-37 данного пособия.
Пример 9 - Расчет индивидуальных и общих индексов
Имеются следующие данные о продаже товаров в магазинах одной сети:
Таблица 11 – Условные данные о продаже товаров
| Товары | Цена за кг., руб. | Продано, тонн | ||
| июль | сентябрь | июль | сентябрь | |
| Картофель | 24 | 18 | 90 | 160 |
| Помидоры | 110 | 70 | 50 | 60 |
Требуется определить:
1. Индивидуальные индексы количества проданных товаров, цен и выручки от продажи. Проверить увязку их в систему.
2. Сводные индексы количества проданного, цен и выручки от продажи. Сделать выводы.
Решение:
1. Определим индивидуальные индексы по каждому виду товаров.
Индивидуальный индекс количества проданных товаров определяется по формуле:
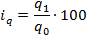
Тогда, индивидуальный индекс количества проданного картофеля равен:
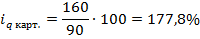
Следовательно, в сентябре продали картофеля на 77,8% больше, чем в июле.
Индивидуальный индекс количества проданных помидоров равен:
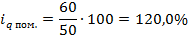
Следовательно, в сентябре продали помидоров на 20,0% больше, чем в июле.
Индивидуальный индекс цен определяется по формуле:
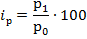
Тогда, индивидуальный индекс цен проданного картофеля равен:
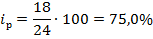
Следовательно, в сентябре картофель стал дешевле на 25,0%, чем в июле (75,0-100,0 = 25,0).
Индивидуальный индекс цен помидоров равен:
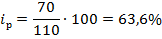
Следовательно, в сентябре помидоры стали дешевле на 36,4%, чем в июле (63,6-100,0 = 36,4).
Индивидуальный индекс выручки от продажи определим по каждому виду продукции по формуле:
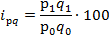
Тогда, индивидуальный индекс выручки от продажи картофеля равен:
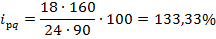
Индивидуальный индекс выручки от продажи помидоров равен:
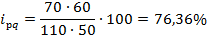
Таким образом, мы видим, что в сентябре выручка от продажи картофеля возросла на 33,3%, а от продажи помидоров сократилась на 23,6%
Проверим увязку индивидуальных индексов в систему:
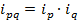
По картофелю: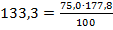 
- равенство верно.
По помидорам: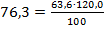 
- равенство верно.
2. Определим сводные индексы количества проданного, цен и выручки от продажи.
Сводный индекс количества проданных товаров определяется на основе построения систем взаимосвязанных индексов. Так как это индекс количественного признака, он рассчитывается по формуле:
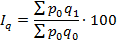
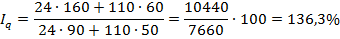
Сводный индекс цен так же определяется на основе построения системы взаимосвязанных индексов. Так как это индекс качественного признака, он рассчитывается по формуле:
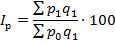
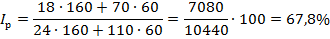
Сводный индекс выручки от продажи является обобщающим индексом, его можно определить двумя способами:
• Как произведение сводных индексов цен и количества проданного товара:
;
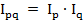• По формуле сводного индекса выручки от продаж:
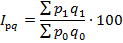
Определим данный индекс, используя оба способа, и сравним полученные результаты.
По первому способу: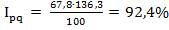 
По второму способу:
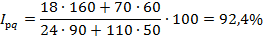
Как мы видим, результат одинаковый.
Выводы: В сентябре по сравнению с июлем выручка от продажи по двум товарам, вместе взятым, сократилась на 7,6% (92,40- 100=7,6). Основной причиной сокращения выступило снижение цен в среднем по двум товарам на 32,2% (67,8 -100 = 32,2), о чем свидетельствует значение сводного индекса цен.
Количество проданного товара в среднем возросло на 36,3% (136,3 -100 = 36,3), вызвав соответствующий рост выручки от продажи.
Примеры решения задач по теме « Выборочное наблюдение»
Понятие выборочного наблюдения, виды и методы расчета ошибок репрезентативности, правила выбора формул для расчета ошибок выборочной средней и выборочной доли альтернативного признака рассмотрены на стр. 38- 43 данного пособия.
Пример 10 - Определение пределов генеральной средней и генеральной доли альтернативного признака
Для изучения распределения работников бюджетной сферы по размерам заработной платы в городе проведено 10%- ное выборочное обследование. В результате учета 900 человек выявлено, что средняя зарплата работников составляет 32500 руб. со средним квадратическим отклонением 4200 руб. Из числа работающих 15% получают зарплату свыше 40 000 руб.
Требуется с вероятностью 0,954 определить пределы среднего размера заработка одного работника бюджетной сферы в городе и пределы доли работников, получающих свыше 40000 руб.
Решение:
В данном примере требуется определить пределы двух величин: среднего значения признака и доли жителей, получающих свыше 40000 руб.
Для исчисления пределов вначале следует рассчитать предельные ошибки выборочной средней и выборочной доли альтернативного признака.
Обозначим символами приведенные в условии цифровые данные.
• Так как объем выборки – 10%, следовательно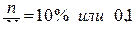 
;
• Учтено 900 человек, т.е. n = 900;
• Средняя зарплата работника - 32500 руб., т.е.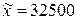 
;
• Среднее квадратическое отклонение – 4200, значит,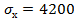 
;
• 15% работающих получают свыше 40000, следовательно, доля альтернативного признака -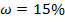 
или 0,15;
• Вероятность расчетов F(t) – 0,954, следовательно, t = 2.
На первом этапе определим среднюю ошибку выборочной средней. Так как в условии не оговаривается, повторный или бесповторный отбор применялся при обследовании, по умолчанию предполагается бесповторный отбор. Объем выборки - 10%, следовательно, для расчета средней ошибки выборочной средней используем формулу (9.5):
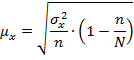
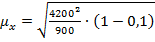=132,8
Определим предельную ошибку выборочной средней, исходя из соотношения:
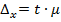
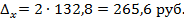
Пределы средней заработной платы работников госсектора определим по формуле:
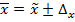
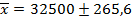
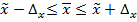
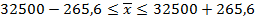
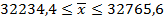
Следовательно, с вероятностью 0,954 (т.е. в 954 случаях из 1000) мы можем утверждать, что средняя зарплата работников госсектора в городе будет не меньше чем 32234,4 руб. и не превысит 32765,6 руб.
На втором этапе определим ошибку доли альтернативного признака.
Начнем с расчета средней ошибки на основе формулы (9.6), так как отбор бесповторный объемом более 5%:
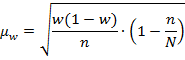
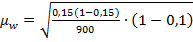=0,0113
Предельная ошибка доли альтернативного признака при вероятности расчетов 0,954 определим, исходя их формулы:
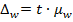
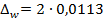
Пределы доли работников госсектора, получающих зарплату свыше 40000 руб., в генеральной совокупности находятся по формуле:
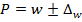
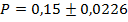
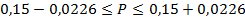
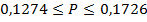
Или, если перевести результаты в процентные соотношения,
. 
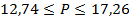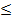
Следовательно, доля работников госсектора, получающих зарплату свыше 40000 руб., колеблется от 12,74% до 17,26%, что можно утверждать с вероятностью 0,954.
Пример 11 - Определение оптимальной численности выборки при расчете доли альтернативного признака
В банке проводится анализ наличия потенциальных кредитных ресурсов. Для этого требуется определить, сколько депозитов из 12500 должно попасть в выборку. Предыдущее обследование показало, что доля невостребованных в срок депозитов составила 27% от их общего числа. Обследование предполагает, что предельная ошибка доли невостребованных депозитов не должна превышать 3%, а вероятность расчетов должна быть не менее 0,997.
Решение:
определим, какие данные имеются в условии:
o N = 12500;
o w = 27%, или 0,27;
o Δw = 3%, или 0,03;
o Вероятность расчетов F(t) – 0,997, следовательно, t = 3.
Т.к. подобные обследования не предполагают повторного отбора, расчет оптимальной численности следует производить по формуле (9.18):
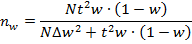
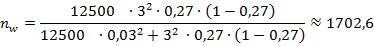
Следовательно, в банке достаточно обследовать 1703 депозита, или 13,6% от их общего числа (1703:12500 · 100 = 13,6%), чтобы определить объем потенциальных кредитных ресурсов.
5 СПИСОК ТЕОРЕТИЧЕСКИХ ВОПРОСОВ
Часть 1 « Общая теория статистики»
1. Предмет и метод статистики.
2. История зарождения и становления статистики как науки.
3. Основные категории статистической науки.
4. Сущность и формы статистического наблюдения.
5. Программа статистического наблюдения.
6. Виды статистического наблюдения.
7. Ошибки статистического наблюдения и способы их устранения.
8. Статистические группировки, их виды и значение.
9. Методика образования групп и интервалов группировки.
10. Правила составления статистических таблиц.
11. Ряды распределения и их графическое изображение.
12. Абсолютные и относительные величины.
13. Сущность средних величин. Виды средних и способы их расчета.
14. Структурные средние - мода и медиана, особенности их расчета в дискретных и интервальных рядах распределения.
15. Показатели вариации: назначение и методы расчета.
16. Понятие о рядах динамики. Статистические показатели динамики.
17. Средние показатели в рядах динамики.
18. Прогнозирование на основе динамических рядов.
19. Изучение сезонных колебаний в рядах динамики.
20. Виды статистических связей и методы их изучения. Понятие стохастической зависимости, виды уравнений регрессии.
21. Определение показателей тесноты связи при линейных и нелинейных стохастических зависимостях (коэффициент линейной корреляции, индекс корреляции, индекс детерминации).
22. Метод сравнения параллельных рядов.
23. Понятие о выборочном наблюдении. Определение ошибки выборки при повторном и бесповторном отборе.
24. Понятие о выборочном наблюдении. Способы отбора единиц при выборочном наблюдении.
25. Понятие о выборочном наблюдении. Определение оптимальной численности выборки.
26. Понятие и сущность индексов. Индивидуальные и общие индексы.
27. Понятие и сущность индексов. Агрегатная форма индексов.
28. Понятие и сущность индексов. Взаимосвязи индексов. Правила построения систем взаимосвязанных индексов.
29. Понятие и сущность индексов. Средние индексы.
30. Понятие и сущность индексов. Индексы средних величин: индексы постоянного состава, переменного состава и структурных сдвигов.
Дата: 2019-05-29, просмотров: 301.
