Цель - освоение приемов выявления стохастических зависимостей между экономическими явлениями, оценки силы и тесноты связей, построения корреляционных моделей.

Содержание темы:

Виды связей. Стохастические зависимости парные и множественные, линейные и криволинейные, прямые и обратные. Методы изучения и измерения взаимосвязей.

Факторный и результативный признаки. Корреляционно-регрессионный анализ связи. Уравнение регрессии и его смысл. Виды уравнений регрессии. Определение параметров уравнения парной регрессии.

Определение показателей тесноты связи при парной корреляции. Коэффициент линейной корреляции и индекс корреляции. Индекс детерминации. Сила связи. Шкала Чеддока.

Использование пакета Microsoft Excel для проведения корреляционно-регрессионного анализа. Расшифровка результатов анализа.

Непараметрические показатели тесноты связи. Метод сравнения параллельных рядов. Коэффициент корреляции рангов Спирмэна.

Показатели тесноты связи между альтернативными признаками – коэффициенты контингенции и ассоциации, методика их расчета и интерпретация результатов.

Методические указания:

Явления экономической жизни, описываемые с помощью определенных статистических показателей, могут состоять между собой в следующих видах связей: балансовой, компонентной и факторной.

Балансовая связь характеризует зависимость между источниками формирования и направлениями использования средств и относятся к аддитивным зависимостям.

Компонентные связи характеризуются тем, что изменение статистических показателей определяется изменением компонентов, входящих в этот показатель как множители. Выражается компонентная связь уравнением:

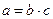
В статистике компонентные связи анализируются обычно при помощи индексного анализа, позволяющего выявить влияние каждого из факторов на изменение обобщающего показателя.

Факторные связи проявляются в согласованной вариации изучаемых показателей, одни из которых выступают как факторные, а другие – как результативные.

Факторные связи делятся на функциональные и стохастические (вероятностные).

Для стохастических связей характерно то, что изменение результативного признака «у» не полностью зависит от влияния факторного признака «х», так как на него могут воздействовать и другие факторы. Поэтому одному значению факторного признака «х» могут соответствовать несколько различных значений результативного признака «у». Следует помнить, что стохастические связи не являются жесткими (полными) зависимостями, они проявляются только в массе случаев, поэтому такие связи могут проявляться только в изменение средних величин факторного и результативного признаков.

В статистике различают парные и множественные стохастические зависимости.

При парной зависимости на результативный признак «у» оказывает влияние только один факторный признак «х». В жизни такая ситуация встречается крайне редко, но при проведении статистических исследований выбирают один наиболее значимый факторный признак, абстрагируясь от возможного влияния других.

Если зависимость множественная, на один результативный признак «у» влияет несколько факторных признаков «х1», «х2», «х3» и т.д.

В зависимости от характера связи между признаками стохастические зависимости делятся на линейные и криволинейные.

Линейная форма связи предполагает равномерное изменение результативного признака под влиянием факторного признака и описывается уравнением линейной регрессии. 

Линейная форма связи делится на прямую и обратную. При прямой форме с возрастанием факторного признака возрастает и результативный признак, при обратной форме связи с ростом факторного признака результативный признак уменьшается.

Помимо линейных зависимостей, в экономике часто встречаются и криволинейные, которые описываются различными уравнениями: параболы любого порядка, гиперболы, степенной, полулогарифмической, показательной и другими функциями.

Корреляционно-регрессионный анализ – один из самых популярных методов анализа связей, позволяющий выявить наличие связи между явлениями, определить тесноту и силу этой связи, подобрать математическую функцию, позволяющую наиболее точно описать связь и проверить надежность произведенных расчетов.

На первом этапе проведения корреляционно-регрессионного анализа необходимо определить вид стохастической зависимости и выбрать самые подходящие уравнения регрессии.

Уравнения регрессии – это математические функции, которые позволяют определить зависимость изменения среднего уровня результативного признака от изменения среднего уровня факторного признака.

На втором этапе рассчитывают параметры выбранного уравнения регрессии, производят оценку их значимости и выбирают то уравнение, которое точнее всего описывает изучаемое явление.

Параметры рассчитываются на основе метода наименьших квадратов. Расчет может производится вручную. В этом случае можно составить систему нормальных уравнений или воспользоваться методом определителей. Формулы уравнений регрессии и методы расчета параметров уравнений регрессии подробно рассмотрены на стр. 113-117 пособия [5].

Значимость параметров уравнения проверяют на основе расчета t- критерия Стьюдента. Рассчитанное по специальным формулам значение t- критерия сравнивают с его табличным значением. Если рассчитанное значение t- критерия больше табличного, параметр считается значимым.

Выбор оптимального уравнения регрессии основан на сравнении показателя, называемого остаточной дисперсией( 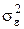). Наиболее точным считается то уравнение, у которого остаточная дисперсия имеет минимальное значение.

В настоящее время для проведения рассмотренных выше процедур рекомендуется воспользоваться пакетом Microsoft Excel. Процедура анализа и расшифровка результатов расчетов рассматривается в [11], на стр. 92-106.

Для определения тесноты связи используются различные показатели: индекс Фехнера, коэффициент линейной корреляции, индекс корреляции (корреляционное отношение), коэффициент корреляции рангов Спирмэна и т.д.

Коэффициент линейной корреляции "r".используется только при линейной форме связи. Он может принимать значения от «минус»1 до 1. Отрицательное значение свидетельствует о наличии обратной связи между признаками «х» и «у». Чем ближе значение «r» к 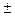1, тем сильнее связь. Если «r» равен 0, связь отсутствует, если «r» равен 1 – связь функциональная.

Индекс корреляции (корреляционное отношение) -R - используется как для линейной, так и нелинейной форм связи. Индекс корреляции принимает значения от 0 до 1.Если показатель тесноты связи будет равен 0, значит связь между «х» и «у» отсутствует, чем ближе к 1, тем теснее связь.

Индекс детерминации (R²⁾ равен отношению факторной и общей дисперсии. Его применяют с целью проверки пригодности рассчитанного уравнения регрессии для практического использования. Если R² ≥ 0,5, модель пригодна для практического применения, так как более половины общей вариации результативного признака объясняется воздействием факторного признака. Более детально данный вопрос рассмотрен на стр. 117-119 пособия [5].

Сила связи находится на основании показателей тесноты связи по шкале Чеддока.

Таблица 6 - Шкала Чеддока

Для определения тесноты связи используются и другие, менее точные показатели, например, коэффициент корреляции рангов Спирмэна ( 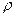). Этот показатель рассчитывается на основе метода выстраивания параллельных рядов и ранжирования значений «х» и «у». Коэффициент Спирмэна может принимать значения от «минус»1 до 1.

Теснота связи альтернативных признаков определяется при помощи коэффициентов ассоциации и контингенции. Данные коэффициенты принимают значения от «минус»1 до 1. Чем ближе значение к 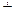1, тем сильнее связь. Методы расчета рассмотренных выше показателей подробно изложены на стр. 120-122 пособия [5].

Вопросы для самоконтроля:

1. Перечислите известные Вам виды связей и укажите методы, применяемые для их анализа

1. Какие статистические методы могут быть использованы для определения наличия связей между явлениями?
2. Охарактеризуйте стохастическую зависимость. Какие методы используются для определения наличия стохастических зависимостей?
3.  Дайте понятие парной и множественной стохастической зависимости.
4. Опишите основные виды уравнений регрессии. От чего зависит выбор уравнения регрессии?
5.  Приведите понятие прямой и обратной зависимости. Какие показатели позволяют определить направление связи?
6. Какие методы используются для определения параметров уравнения регрессии?
7. Какие показатели тесноты связи используются при линейных зависимостях?
8. Какие показатели тесноты связи используются при нелинейных зависимостях?
9. Дайте определение альтернативного признака. Какие показатели используются для определения тесноты связи между альтернативными признаками?

Литература:[2], [5], [8], [10], [11], [12], [13], [14].

Интернет – ресурсы: [1], [2], [5], [6].

РАЗДЕЛ 2  «СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СТАТИСТИКА»