Цель-освоение методов расчета ошибок репрезентативности, распространения результатов выборочного обследования на генеральную совокупность.
Содержание темы:
Причины и условия применения выборочного метода. Понятие генеральной и выборочной совокупностей. Виды выборок. Ошибки выборки и их виды. Средняя и предельная ошибки выборки. Коэффициент доверия.
Понятие доли альтернативного признака, дисперсия доли альтернативного признака. Определение средней и предельной ошибки доли альтернативного признака.
Определение оптимальной численности выборки. Способы отбора единиц из генеральной совокупности и их влияние на величину ошибки выборки.
Методические указания:
При изучении данной темы студенты должны понимать, что в статистике могут применяться два способа сбора информации – сплошное наблюдение и несплошное, основной разновидностью которого выступает выборочное наблюдение.
Под выборочным наблюдением понимается метод исследования, связанный с установлением обобщающих показателей совокупности по некоторой ее части на основе метода случайного отбора. При выборочном наблюдении обследованию подвергается сравнительно небольшая часть всей совокупности (10 – 15%).
Вся совокупность, подлежащая обследованию, называется генеральной совокупностью. Отобранная из генеральной совокупности часть единиц, непосредственно подвергающаяся обследованию, называется выборочной совокупностью или выборкой.
Выборочное наблюдение основано на принципе равной возможности попадания единиц из генеральной совокупности в выборочную совокупность. Это позволяет избежать систематических ошибок наблюдения.
Однако, в связи с тем, что исследуемая совокупность состоит из единиц с варьирующими признаками, состав выборки может отличаться от состава генеральной совокупности, вызывая расхождение между генеральными и выборочными характеристиками. Такие расхождения называются ошибками репрезентативности или ошибками выборки, на определение величины которой обращается особое внимание в данной теме.
Виды выборочного наблюдения классифицируются в зависимости от состава единиц совокупности, от повторности, от способа отбора, от характера отбора, от числа ступеней отбора, и др. признаков. Классификация видов выборочного наблюдения подробно рассмотрена на стр. 101-103 пособия [5].
При использовании выборочного наблюдения можно рассчитать две основные характеристики - среднее значение показателя в выборочной совокупности и долю единиц совокупности, обладающих альтернативным признаком. Методика расчета среднего значения признака подробно рассмотрена в теме 5.
Доля единиц, обладающих альтернативным признаком, в генеральной совокупности определяется следующим образом:
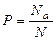 (9.1)
(9.1)
где Р – доля альтернативного признака в генеральной совокупности;
Na – численность единиц, обладающих альтернативным признаком, в генеральной совокупности;
N – общая численность единиц в генеральной совокупности.
В выборочной совокупности доля единиц, обладающих альтернативным признаком, определяется аналогично:
 (9.2)
(9.2)
Данные характеристики, полученные при выборочном обследовании, будут отличаться от характеристик генеральной совокупности на величину ошибки репрезентативности. Таким образом, в ходе выборочного наблюдения можно определить ошибку репрезентативности выборочной средней и ошибку репрезентативности доли альтернативного признака.
В статистике выделяют два вида ошибки репрезентативности – среднюю и предельную.
В таблице 3 приведены основные виды формул, используемых для расчета средней ошибки выборки и средней ошибки доли альтернативного признака.
Таблица 3 - Формулы для расчета средней ошибки репрезентативности
| Вид отбора и объем выборочной совокупности | Средняя ошибка выборочной средней | Средняя ошибка доли альтернативного признака | ||
| Формула | Номер формулы | Формула | Номер формулы | |
| 1 | 2 | 3 | 4 | 5 |
| Повторный отбор (бесповторный объемом до 5%) | 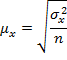
| (9.3) | 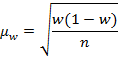
| (9.4) |
| Бесповторный отбор объемом свыше 5% | 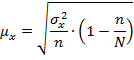
| (9.5) | 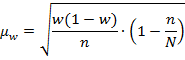
| (9.6) |
| Малая выборка | 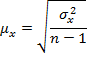
| (9.7) | 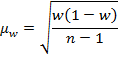
| (9.8) |
где 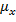 – средняя ошибка выборочной средней;
– средняя ошибка выборочной средней;
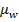 - средняя ошибка доли альтернативного признака;
- средняя ошибка доли альтернативного признака;
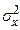 - дисперсия;
- дисперсия;
n- объем выборки;
N – объем генеральной совокупности;
w - доля альтернативного признака в выборочной совокупности.
При определении ошибки выборки следует обратить внимание, что выбор формулы для ее расчета зависит от двух факторов:
· Способа формирования выборочной совокупности. Она может быть сформирована посредством повторного отбора, при котором обследованные единицы возвращаются в генеральную совокупность и, вследствие этого, могут участвовать в обследовании неоднократно, что существенно ухудшает качество выборочных характеристик. При использовании бесповторного отбора, для которого характерно исключение обследованных единиц из генеральной совокупности, выборочные характеристики имеют большую точность.
· Объема выборочной совокупности. Если из генеральной совокупности отбирается для обследования более 5% единиц, следует делать поправку на изменение объема генеральной совокупности.
В статистике используется понятие малой выборки, которое не связано с особенностями формирования выборочной совокупности, а только с тем, что ее численность не превышает 30 единиц. Ошибка выборки в этом случае будет заведомо больше и для ее расчета используются специальные формулы.
Средняя ошибка выборки совпадает с реальной только в 683 случаях из 1000. Если хотят получить результат с большей надежностью, используют предельную ошибку репрезентативности 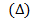 .Предельная ошибка позволяет определить границы среднего значения признака в генеральной совокупности с заданной степенью вероятности. Для ее определения среднюю ошибку увеличивают в t раз, где t - коэффициент доверия.
.Предельная ошибка позволяет определить границы среднего значения признака в генеральной совокупности с заданной степенью вероятности. Для ее определения среднюю ошибку увеличивают в t раз, где t - коэффициент доверия.
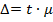 (9.9)
(9.9)
где t - коэффициент доверия;
μ - средняя ошибка репрезентативности.
Определить значение коэффициента доверия при любой степени вероятности можно на основе таблицы функции Лапласа. Выписка из таблицы функции Лапласа приведена в таблице 4.
Таблица 4 - Выписка из таблицы функции Лапласа
| F(t) | t | F(t) | t | F(t) | t | F(t) | t |
| 0,663 | 0,96 | 0,911 | 1,70 | 0,932 | 1,83 | 0,947 | 1,94 |
| 0,676 | 0,99 | 0,920 | 1,75 | 0,937 | 1,86 | 0,954 | 2,00 |
| 0,854 | 1,46 | 0,929 | 1,81 | 0,942 | 1,92 | 0,997 | 3,00 |
Подставляя в выражение (9.9) значение средней ошибки выборочной средней из таблицы 3, можно получить формулы предельной ошибки для каждого вида отбора. Например, для повторного отбора предельная ошибка выборочной средней 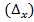 примет вид:
примет вид:
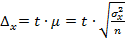 (9.10)
(9.10)
Остальные виды предельных ошибок получают аналогично.
Следует иметь ввиду, что определение ошибки репрезентативности является промежуточным этапом выборочного наблюдения. Величина предельной ошибки используется для расчета характеристик генеральной совокупности – генеральной средней и генеральной доли альтернативного признака.
Определить дискретное значение генеральных характеристик невозможно, поэтому производится расчет пределов генеральной средней и генеральной доли альтернативного признака, т.е. определяются границы, в которых заключены данные характеристики.
При использовании предельной ошибки репрезентативности пределы генеральной средней определяются следующим образом:
 (9.11)
(9.11)
или 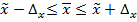 (9.12)
(9.12)
Пределы генеральной доли альтернативного признака определяются аналогично:
 (9.13)
(9.13)
или 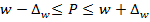 (9.14)
(9.14)
В ходе выборочного наблюдения одним из вопросов является определение объема выборочной совокупности. Определить оптимальную численность можно, используя формулу предельной ошибки репрезентативности, следовательно, выбор формулы зависит от способа формирования выборочной совокупности. В таблице 5 приведены формулы для определения оптимальной численности выборки при каждом способе отбора для расчета выборочной средней и выборочной доли альтернативного признака.
Следует помнить, что расчет оптимальной численности возможен только в том случае, когда изначально известны величины дисперсии и предельной ошибки репрезентативности. Поэтому определять оптимальную численность рекомендуется только при проведении повторных выборочных наблюдений.
Таблица 5 - Формулы для расчета оптимальной численности выборки
| Вид отбора и объем выборочной совокупности | Для выборочной средней | Для доли альтернативного признака | ||
| Формула | Номер формулы | Формула | Номер формулы | |
| 1 | 2 | 3 | 4 | 5 |
| Повторный отбор | 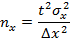
| (9.15) | 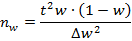
| (9.16) |
| Бесповторный отбор | 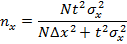
| (9.17) | 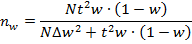
| (9.18) |
где nx , nw - оптимальная численность выборки;
t - коэффициент доверия;
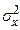 - дисперсия;
- дисперсия;
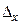 - предельная ошибка выборки;
- предельная ошибка выборки;
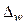 - предельная ошибка доли альтернативного признака;
- предельная ошибка доли альтернативного признака;
N – объем генеральной совокупности;
w - доля альтернативного признака в выборочной совокупности.
Вопросы для самоконтроля:
1. Охарактеризуйте выборочное наблюдение, изложите его основные преимущества по сравнению со сплошным наблюдением.
2. Дайте понятие генеральной и выборочной совокупностей. Какова причина возникновения ошибки репрезентативности?
3. Перечислите основные виды выборочного наблюдения. Охарактеризуйте каждый из них.
4. На каких принципах базируется стратифицированный отбор? Какой принцип является оптимальным?
5. Дайте понятие многоступенчатого отбора. Как формируется выборка при многоступенчатом отборе?
6. От каких факторов зависит выбор формулы средней ошибки репрезентативности? Напишите формулу расчета средней ошибки выборки при повторном отборе.
7. Дайте понятие коэффициента доверия. Как он определяется?
8. Как определить пределы среднего значения признака в генеральной совокупности?
9. Какова цель определения оптимальной численности выборки?
Литература:[2], [5], [8], [10], [11], [12], [13], [14].
Интернет – ресурсы: [1], [5], [6].
Дата: 2019-05-29, просмотров: 472.