Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Цель - освоение приемов графического изображения массивов статистических данных и результатов статистического анализа.

Содержание темы:

Понятие, назначение и составные элементы статистических графиков, классификация графиков.

Построение и оформление статистических графиков на основе реальных статистических показателей с использованием пакета MicrosoftExcel.

Методические указания:

При изучении данной темы студенты должны уяснить, что статистические графики являются одной из форм представления результатов статистического наблюдения и анализа.

Статистические графики являются средством повышения доступности уровня восприятия статистической информации, а также приемом одновременного восприятия большого числа статистических показателей. Следует помнить, что одновременное изображение более 7 элементов на одном графике существенно затрудняет его восприятие и анализ.

Студентам следует разобрать такие категории, как графический образ, поле графика, масштабные ориентиры, экспликация графика.

Основное внимание следует уделить классификации статистических графиков, в частности, понятию статистических карт (картограмм и картодиаграмм). При изучении диаграмм рекомендуется разобрать различия и область применения каждого вида диаграмм – линейных, точечных, фигурных, полосовых, секторных, радиальных и т.д.

В настоящее время широкое применение в статистическом анализе получили графики, позволяющие анализировать многомерные стохастические зависимости, в частности «Лица Чернова», «лучи» и «звезды» и другие виды корреляционных графиков.

Одним из популярных приемов графического анализа является «Знак Варзара». Следует обратить внимание на особенности его построения и применения.

Следует иметь ввиду, что применение современных средств вычислительной техники существенно облегчает построение статистических графиков, поэтому рекомендуется самостоятельно разобрать алгоритм построения графиков разного типа при помощи стандартного программного обеспечения - Microsoft Excel

Вопросы для самоконтроля:

1. Дайте определение статистического графика.

2. Приведите определение графического образа.

3. Как называется схематическая географическая карта, на которую наложены статистические диаграммы?

4. Как называется часть графика, включающая его название и пояснения отдельных частей?

5. Какие виды графиков используются для изображения динамики явления?

Литература: [11], [13].

Интернет-ресурсы: [3], [4].

Тема 7 « Анализ рядов динамики »

Цель - освоение приемов анализа динамических процессов в экономике, методик выявления трендов и построения трендовых моделей.

Содержание темы:

Понятие о рядах динамики. Правила построения и анализа рядов динамики. Виды рядов динамики.

 Основные показатели, определяемые для динамических рядов. Средние характеристики рядов динамики, методы их расчета.

Прогнозирование методом экстраполяции.

Методы выявление основной тенденции развития – метод укрупнения интервалов, скользящей средней, аналитического выравнивания.

 

Методические указания:

Ряд динамики— числовые значения статистического показате­ля, представленные во временной последовательности. Ряд динамики состо­ит из двух элементов - временной компоненты, в которой указываются периоды (или даты), и уровней ряда - показателей, характеризующие изучаемый объект за эти периоды (или на эти даты).

Ряды динамики могут быть двух видов: интервальные и моментные.

Особенностью интервальных рядов из абсо­лютных величин является то, что их уровни можно суммировать, получая новые численные значения объема явления, относящиеся к более длительным периодам.

В моментном ряду динамики приводятся данные, характеризу­ющие размеры явления на определенные моменты (даты) време­ни.

Важнейшим условием правильного формирования рядов ди­намики является сопоставимость уровней, образующих ряд. Основ­ным требованием сопоставимости уровней является одинаковая методология их исчисления для всех периодов или дат. Условием сопоставимости дан­ных является также одинаковая полнота охвата различных частей явления, представленного рядом динамики.

Специальным условием сопоставимости абсолютных величин интервального динамического ряда является равенство периодов, за которые приводятся данные.

Для изучения интенсивности изменения уровней ряда во вре­мени исчисляются следующие аналитические показатели динамики:

· абсолют­ный прирост (сокращение);

· темп роста (сокращения);

· темп приро­ста(сокращения);

· абсолютное значение одного процента прироста.

Следует обратить внимание, что перечисленные показатели динамики можно исчислять с пере­менной или постоянной базой. Если производится сравнение каж­дого уровня с предыдущим уровнем, то получаются показатели ди­намики с переменной базой (цепные показатели динамики). Если каждый уровень сравнивается с начальным уровнем или каким-то другим, принятым за базу сравнения, то получаются показатели динамики с постоянной базой (базисные показатели динамики).

В данной теме используются следующие условные обозначения:

• Δу - абсолютный прирост (сокращение);

• у_i - уровень ряда в сравниваемом периоде;

• у_б - уровень явления в периоде, принятом за базу сравнения;

• у _{i -1}- уровень явления в период, предшествующий сравниваемому.

 

1. Абсолютный прирост (сокращение) 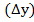. Показывает, на сколько единиц изменился уровень явления в изучаемом периоде по сравнению с периодом, принятым за базу сравнения. Абсолютный прирост (сокращение) может быть положительным или отрицательным. Положительный знак указывает на рост явления, отрицательный – на сокращение.

 

базисный 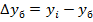                              (7.1)

цепной 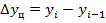                                  (7.2)

 

Между цепными и базисными абсолютными приростами существует следующая зависимость: сумма цепных приростов в полном ряду динамики равна последнему базисному абсолютному приросту:

                                    (7.3)

 

2.Темп роста (снижения) ). Показывает, во сколько раз возрос или сократился уровень явления в изучаемом периоде по сравнению с периодом, принятым за базу сравнения. Показатель рассчитывается в долях единицы или процентах. Если темп роста (сокращения) больше 1 (100%) – это свидетельствует о росте явления, если меньше 1 (100%) – о сокращении.

 Если явление в изучаемом периоде не изменилось по сравнению с базисным периодом, темп роста будет равен 1 (100%).

 

базисный 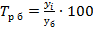                             (7.4)

цепной 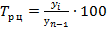                               (7.5)

 

Цепные и базисные темпы роста связаны следующим образом: произведение цепных темпов роста в полном ряду динамики равно последнему базисному темпу роста:

ПТ_{р ц} = Т_{р б п}                                             (7.6)

 

3.Темп прироста (сокращения) 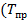). Показывает, на сколько процентов изменился уровень явления в изучаемом периоде по сравнению с периодом, принятым за базу сравнения. Показатель рассчитывается в процентах или долях единицы. Направление изменения показывает знак: положительный – рост, отрицательный – сокращение.

базисный 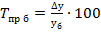                                (7.7)

 

цепной 8)

 

или            Т_пр = Т_р – 1 ( если темп роста рассчитан в долях единицы)

 

Т_пр = Т_р – 100 ( если темп роста рассчитан в процентах) (7.9)

 

4. Абсолютное значение 1 % прироста( 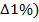. Находится как частное от деления абсолютного прироста на темп прироста. Показывает, какая абсолютная величина скрывается за относительным показателем – 1% прироста.

 

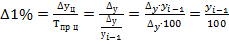                       (7.10)

 

Таким образом, абсолютное значение 1% прироста можно вычислить как одну сотую от базисного уровня. Этот показатель рассчитывается только для цепных показателей динамики.

Для характеристики интенсивности развития за длительный период рассчитываются средние показатели динамики:

1. Средний уровень ряда;

2. Средний абсолютный прирост;

3. Средний темп роста;

4. Средний темп прироста.

В данном разделе используются следующие условные обозначения:

· у_i- уровень ряда в i-м периоде;

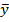·  - средний уровень ряда;

· n - количество уровней в ряду динамики;

· - средний абсолютный прирост;

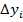·  - цепной абсолютный прирост в i-м периоде;

· k - количество абсолютных приростов или темпов роста в изучаемом ряду динамики;

· y_n - последний уровень ряда динамики;

· T_p - темп роста;

· - средний темп прироста;

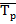· - средний темп роста.

 

1.  Расчет среднего уровня в рядах динамики зависит от вида ряда.

В интервальном ряду (полном и неполном) средний уровень 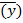рассчитывается по формуле средней арифметической простой:

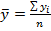                                       (7.11)

 

В моментном ряду динамики расчет среднего уровня зависит от того, полный он или нет. В полном ряду средний уровень 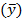рассчитывается по формуле средней хронологической:

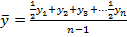                          (7.12)

 

Если моментный ряд неполный, то средний уровень 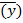находится по формуле средней арифметической взвешенной:

 

 

где у _i – уровень ряда, сохранявшийся без изменения в течение времени t_i .

 

2.Средний абсолютный прирост ( 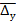)может быть найден двумя методами:

                                            (7.14)

                                               

 

Следует иметь виду, что формула (7.14) может быть использована только в полных рядах динамики, а формула (7.15) – в любых рядах динамики.

 

3. Средний темп роста 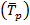также может быть определен двумя методами:

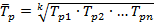                                      (7.16)

 

                       или                                                  (7.17)         

 

Следует иметь виду, что формула (7.16) может быть использована только в полных рядах динамики, а формула (7.17) – в любых рядах динамики.

 

4.Средний темп прироста  :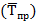

 

Формула (7.18) используется в том случае, если темп роста средний рассчитан в долях единицы.                    

Если темп роста средний рассчитан в процентах, используется формула:

 

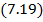
Используя характеристики динамических рядов, можно прогнозировать уровни явления в будущем или определять недостающие характеристики внутри ряда.

Нахождение по имеющимся данным за определенный период времени некоторых недостающих значений признака внутри это­го периода называется интерполяцией. Нахождение значений признака за пределами анализируемого периода называется экс­траполяцией.

Применение экстраполяции для прогнозирования должно ос­новываться на предположении, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ря­да, т.е. в будущем. Метод экстраполяции основан на использовании средних показателей динамики – среднего темпа роста или среднего абсолютного прироста.

При выборе метода прогнозирования исходят из следующего правила: если явление имеет равномерный характер развития, т.е. примерно равны абсолютные приросты, для прогнозирования используется следующая формула:

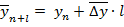                             (7.20)

 

где y_n - последний известный уровень ряда динамики;

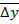- средний абсолютный прирост в анализируемом ряду динамики;

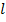 - срок прогноза.

 

     Если явление имеет равноускоренный характер развития, т.е. примерно равны темпы роста, перспективное значение определим следующим образом:

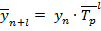                                    (7.21)

             

где  - средний темп роста.

 

Одним из основных назначений динамических рядов является определение обшей тенденции изменения явления – тренда. Выявляется тренд несколькими способами – способом укрупнения интервалов, способом скользящей средней, методом аналитического выравнивания или графическим способом.

Наиболее простым способом является укрупнение интервалов и определение итога уровня для этих интервалов. Исчисление итогов за ук­рупненный период возможно только по интервальным рядам аб­солютных величин.

Скользящая средняя— подвижная динамическая средняя, ко­торая исчисляется по ряду при последовательном передвижении на один интервал, т. е. сначала вычисляют средний уровень из оп­ределенного числа первых по порядку уровней ряда, затем - сред­ний уровень из такого же числа членов, начиная со второго. Если в ряду динамики имеются периодические колебания, то период скользящей средней должен совпадать с периодом колебания или быть кратным ему. Более детально данный вопрос рассматривается в пособии [5] на стр. 67-68.

Получить описание плав­ной линии развития (тренда) динамического ряда можно только при помощи аналитического выравнивания, сущность которого за­ключается в нахождении уравнения, выражающего закономер­ность изменения явления как функцию времени ŷ _t = f ( t ).

Вид уравнения определяется характером динамики развития конкретного явления. На практике выбор формы кривой может быть основан на анализе графического изображения уровней динамического ряда (линейной диаграммы), при этом целесообразнее воспользовать­ся графическим изображением сглаженных уровней, в которых случайные колебания погашены.

Аналитическое сглаживание позволяет не только определить общую тенденцию изменения явления на рассматриваемом от­резке времени, но и выполнять расчеты для таких периодов, в от­ношении которых нет исходных данных.

Принципы проведения аналитического выравнивания подробно рассмотрены в пособии [5] на стр. 69-70.

 

Вопросы для самоконтроля:

1.Какие основные методологические принципы положены в основу построения динамических рядов? В чем отличие моментного ряда динамики от интервального ряда?

2. Какие существуют методы приведения уровней динамического ряда к сопоставимому виду?

3.Какие статистические показатели используются для анализа динамики?

4. Какие показатели применяет статистика для измерения среднего уровня моментного ряда динамики?

5. Приведите основные формулы расчета показателей среднего уровня интервального ряда динамики?

6.В чем заключается сущность метода смыкания динамических рядов? В каких ситуациях необходимо использовать этот метод?

7. Какие методы выявления основной тенденции ( тренда) используются в статистике?

8.Какие виды средних величин используются при анализе рядов динамики абсолютных и относительных величин? Приведите основные формулы их расчета.

10. В чем заключается сущность метода экстраполяции, для чего статистика использует этот метод?

 

Литература:[2], [5], [8], [10], [11], [12], [13], [14].

Интернет – ресурсы: [1], [5], [6].