Домашняя контрольная работа была проведена после завершающего четвертого занятия перед написанием итоговой контрольной работы.

Содержание:

1. Решите уравнение .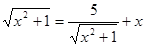

2. Решите уравнение .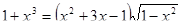

3. Решите уравнение .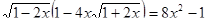

4. Найдите наибольшее и наименьшее значения выражения 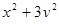 в области .

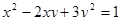Результаты:

	Фамилия	1 задание	2 задание	3 задание	4 задание
1	Бакулин	+д	+	+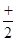
2	Бизяев	+д	+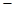
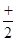
3	Витвицкий	+	+к	+	+
4	Громазин	+	+	+	–
5	Давидюк	+	+	+	*
6	Жичкина	–с	+	+	–
7	Журавлев	+	+	+	*
8	Коновалов	+	+	+	+
9	Коробейников	+с	+	+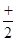
10	Макарова	+	+	+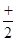
11	Новоселов	+	+	–	*
12	Овчинников	+	+		+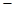
13	Прокашев	+	+	+	+
14	Сероглазов	+д	+	+	*
15	Скачилова	+	+	+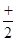
16	Хохлов	+д	+	+	+
17	Черняк	+с	+	+
18	Шильников	+	+	+	*
Процент учащихся, верно выполнивших задание		94%	100%	83%	89%
Процент учащихся, выбравших тригонометрическую подстановку		72%	100%	100%	100%
Процент учащихся, верно решивших с помощью тригонометрической подстановки		92%	100%	83%	89%
Процент учащихся, обосновавших введение тригонометрической подстановки		100%	100%	100%	56%
Процент учащихся, верно решивших другим способом		87,5%	–	–	–
Процент учащихся, решавших двумя способами		17%	0%	0%	0%

Первые три задания были посвящены решению иррациональных уравнений. Причем решить первое уравнение было рекомендовано двумя способами: с помощью тригонометрической подстановки и без нее. Это было сделано с той целью, чтобы показать учащимся: не всегда введение тригонометрической подстановки упрощает решение. Иногда применение стандартного метода для решения задач оказывается более эффективным. Таким образом, уравнение было призвано обратить внимание учащихся не необходимость обдуманного введения тригонометрической подстановки. Пример не вызвал серьезных затруднений, из восемнадцати работ только в одной были ошибки. Как правило, для решения учащиеся выбирали и обосновывали подстановку

.

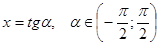Одним учащимся был предложен другой вариант тригонометрической подстановки

,

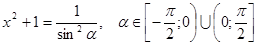но само решение оказалось более громоздким.

Со вторым заданием справились все учащиеся.

В третьем задании ошибки возникли у трех учащихся из восемнадцати и были связаны с неверным отбором корней.

Вновь наибольшие затруднения вызвало задание на нахождение наибольшего и наименьшего значений выражения. Даже среди тех, кто получил верный ответ, немногие обосновали введение тригонометрической подстановки.