Задачи, связанные с поиском наибольшего и наименьшего значений функции, неспроста пользуются большой популярностью у составителей экзаменационных заданий: чтобы решить подобную задачу, приходится комбинировать приемы и методы из весьма различных разделов школьного курса математики. Первое, что приходит в голову при решении подобных задач, – исследовать функцию на наибольшее и наименьшее значения с помощью производной. Но у такого подхода есть недостаток: во многих задачах вступительных экзаменов в вузы с повышенными требованиями по математике этот привычный путь решения сопряжен со значительными техническими трудностями. В условиях конкурса этот недостаток особенно ощутим. Часто, однако, удается избавиться от громоздких выкладок, применяя понятия и навыки из других разделов школьного курса математики. Например, из тригонометрии.
Пример 1. Найти наибольшее и наименьшее значение выражения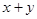 
в области
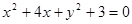[25].
Решение с помощью тригонометрической подстановки
Уравнение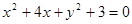 
преобразуем так, чтобы в левой части получилась сумма квадратов: 
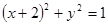. Следовательно, каждое из выражени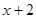й 
и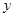 
по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Положим 
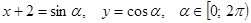. Выразим 
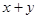через одну величину 
:
.
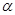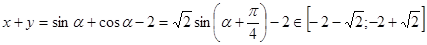Ответ: наибольшее значение равно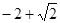 
, наименьшее значение равно 
.
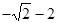Алгебраическое решение
Уравнение 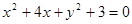преобразуем так, чтобы в левой части получилась сумма квадратов: 
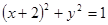. Нам нужно найти наибольшее и наименьшее значения выражения 
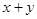в точках окружности 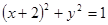, то есть окружности с центром в точке 
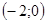и радиусом 
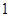. Пусть в точке с координатами 
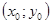выражение 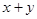принимает наибольшее значение, тогда справедлива система
.
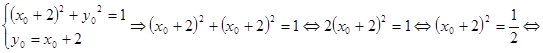
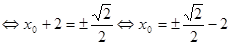Так как ищем наибольшее значение выражения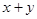 
, то выбираем
.
.
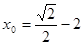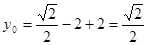Тогда наибольшее значение выражения 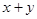равно
.
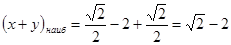Аналогично находим, что наименьшее значение выражения 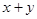равно
.
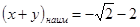Ответ: наибольшее значение равно 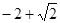, наименьшее значение равно 
.
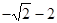Пример 2. Найти наименьшее и наибольшее значения выражения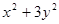 
, если 
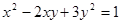[24].
Решение с помощью тригонометрической подстановки
Уравнение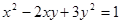 
преобразуем так, чтобы в левой части получилась сумма квадратов:
.
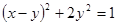Имеем, что сумма квадратов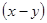 
и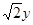 
равна единице, поэтому каждое из этих выражений по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Вот почему можно положить 
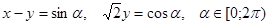. Выразим сумму квадратов 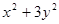через одну величину 
:
.
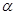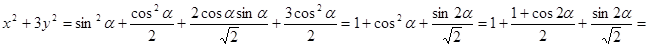
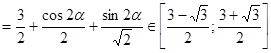Ответ: наименьшее значение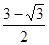 
, наибольшее значение 
.
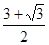Алгебраическое решение
Иногда уравнения с параметрами возникают при решении задач, казалось бы, не имеющих к ним никакого отношения. Если требуется найти, например, наименьшее значение функции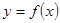 
, ответ можно получить, если найти множество всех ее значений. Хотя это и более общая задача, но ее решение оказывается более простым. Причем число 
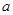будет значением функции 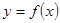тогда и только тогда, когда уравнение 
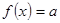имеет хотя бы один корень. Поэтому требуется найти все такие значения параметра 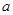и среди них выбрать наименьшее число. Это число и будет наименьшим значением функции 
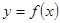[37]. Реализуем сказанное для решения данной задачи другим способом.
Перейдем к системе
,
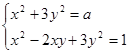то есть выясним, при каких значениях параметра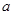 
система имеет решения. Умножим второе уравнение на 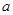и вычтем полученное уравнение из первого.
.
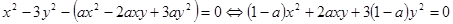Получили однородное уравнение относительно переменных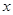 
и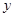 
. Проверкой устанавливается, что при 
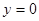система решений не имеет, поэтому уравнение можно разделить на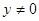 
.
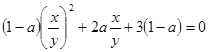Чтобы это уравнение имело решения необходимо и достаточно, чтобы его дискриминант был неотрицателен.
.
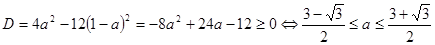Итак, данная система равносильна системе
.
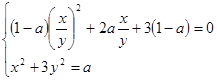Покажем, что при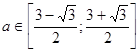 
система имеет решения. Пусть 
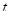- корень первого уравнения, тогда 
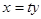подставим во второе уравнение
.
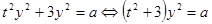Обратим внимание на то, что в промежутке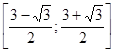 
только положительные числа, значит, полученное уравнение имеет решения. Соответственно, имеет решение и вся система. Промежуток 
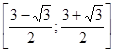и есть множество значений, принимаемых выражением 
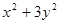при условии, что
.
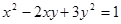В данном случае решение с помощью тригонометрической подстановки проще как в техническом, так и в идейном смысле. Не зная заранее идеи второго способа, трудно догадаться свести задачу о нахождении наибольшего и наименьшего значений выражения к решению системы с параметром.
Пример 3. Найти наибольшее и наименьшее значение выражения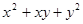 
, если 
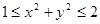[16].
Как в предыдущем примере, в этом случае самый удобный подход – тригонометрическая подстановка. Решение системы, состоящей из двух неравенств и одного уравнения с параметром, довольно сложно.
Решение с помощью тригонометрической подстановки
Положим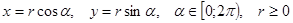 
. Геометрический смысл такой замены: для каждой точки 
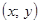кольца 
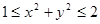определяются расстояние 
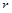до начала координат и угол 
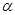наклона вектора 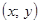к положительному направлению оси абсцисс. Тогда неравенство 
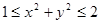будет выполнено при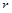 
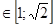. Произведем замену в данном выражении
= 
.
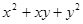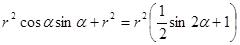Так как множество значений выражения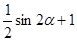 
– это отрезок 
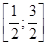, то множество значений выражения 
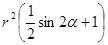– отрезок 
.
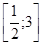Ответ: наименьшее значение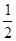 
, наибольшее значение 3.
Пример 4. Среди всех решений системы
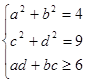[42].
Найдите такие, при которых выражение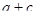 
принимает наибольшее значение.
Перепишем систему в виде
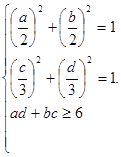
Так как сумма квадратов чисел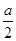 
и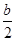 
рана единице, то каждое из них по абсолютной величине не превосходит единицы, поэтому их можно рассматривать как синус и косинус некоторого аргумента. Вот почему будет законна подстановка 
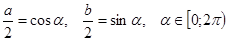. Аналогично обосновывается введение замены 
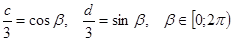. Тогда неравенство системы перепишется в виде
.
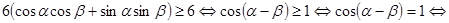
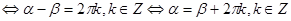Запишем выражение 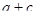в виде
.
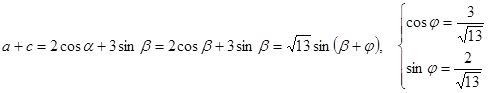Наибольшее значение выражения 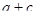достигается тогда и только тогда, когда
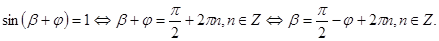
Найдем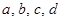 
.
.
.
.
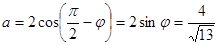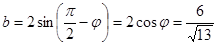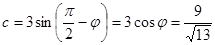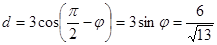Ответ: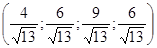 
.
Алгебраическое решение
Перепишем исходную систему в виде
.
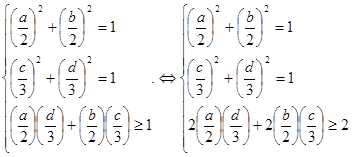Сложим равенства полученной системы
.
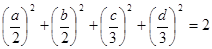Сравним левые и правые части получившегося равенства и неравенства системы, получим
.
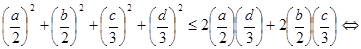
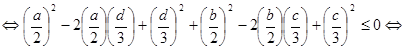
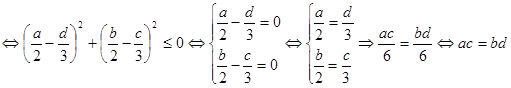Рассмотрим квадрат выражения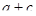 
.
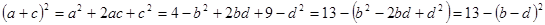Наибольшее значение выражения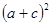 
, а значит, наибольшее значение выражения 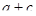имеет место тогда и только тогда, когда 
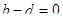, то есть 
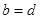. Можно записать
.
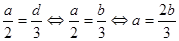Подставим полученное выражение 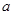в первое уравнение исходной системы и найдем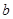 
.
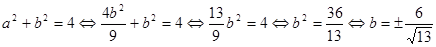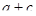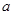Так как необходимо найти наибольшее значение выражения и и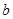 
имеют одинаковый знак, то выбираем
.
.
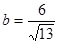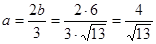Так как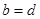 
, то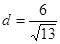 
.
.
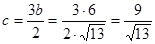Ответ: .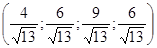
Здесь решение с помощью тригонометрической подстановки компактнее, быстрее приводит к результату. Единственный и важный момент, на который следует указать учащимся, является необходимость обоснования введения тригонометрической подстановки. Тот факт, что, например,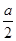 
и 
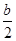по модулю не превосходят единицы, можно проиллюстрировать графически. Уравнение 
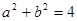задает окружность с центром в начале координат и радиуса 2.
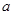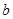Из рисунка видно, что и принимают значения из отрезка 
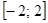, тогда 
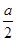и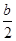 
изменяются на отрезке 
.
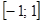§5. Решение задач с параметрами
Решение задач с параметрами – один из труднейших разделов школьного курса математики. Здесь, кроме использования определенных алгоритмов решения уравнений или неравенств, приходится думать об удачной классификации, следить за тем, чтобы не пропустить много тонкостей. Уравнения и неравенства с параметрами – это тема, на которой проверяется подлинное понимание учеником материала. Поэтому, например, на вступительных экзаменах в вузы с повышенными требованиями по математике уравнения и неравенства с параметрами часто включают в варианты письменных работ.
Пример 1. Решите и исследуйте уравнение
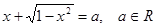[45].
Решение с помощью тригонометрической подстановки
Так как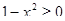 
, то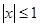 
, поэтому положим 
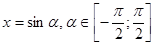. Уравнение примет вид
.
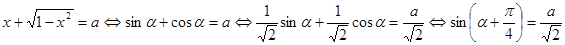Если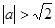 
, то данное уравнение корней не имеет.
Пусть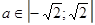 
. Так как 
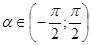, то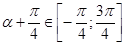 
. При этих значениях 
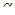имеем
.
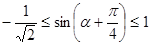То есть для того чтобы уравнение имело корни необходимо и достаточно, чтобы
.
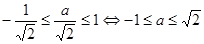Значит, если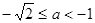 
, то данное уравнение корней не имеет.
Пусть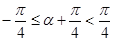 
, то есть 
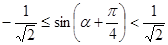. Отсюда 
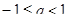. Тогда данное уравнение имеет один корень
.
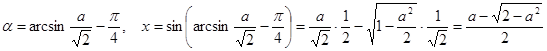Если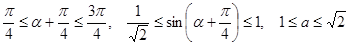 
, то исходное уравнение имеет два корня
.
, 
.
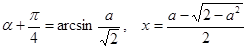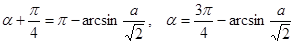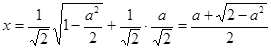Ответ: Ес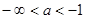ли 
или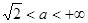 
, то данное уравнение корней не имеет.
Если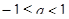 
, то уравнение имеет единственный корень 
.
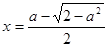Если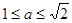 
, то уравнение имеет два корня 
.
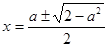Алгебраическое решение
.
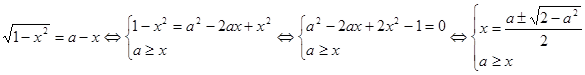Пусть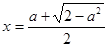 
. Выясним, при каких значениях 
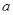выполняется неравенство 
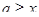, то есть решим неравенство
.
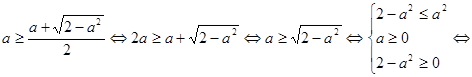
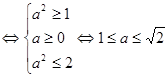Пусть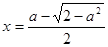 
, тогда рассмотрим неравенство
.
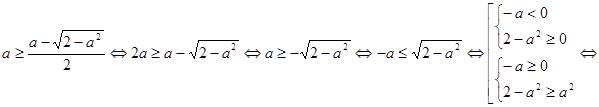
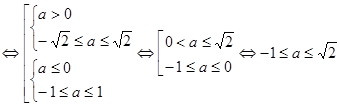Ответ: Ес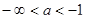ли 
или 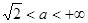, то данное уравнение корней не имеет.
Если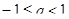 
, то уравнение имеет единственный корень 
.
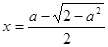Если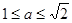 
, то уравнение имеет два корня 
.
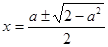В данном случае оба решения равноценны, можно решать любым способом. Зато уже в следующем примере решение с помощью тригонометрической подстановки проще.
Пример 2. При каких а неравенство
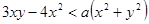
имеет решение [13].
Неравенство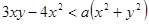 
имеет решение при а большем наименьшего значения выражения 
.
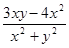Решение с помощью тригонометрической подстановки
Положим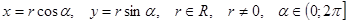 
, тогда
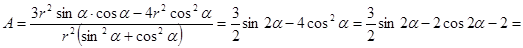
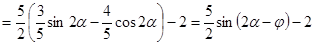, где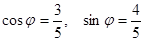 
.
Оценим выражение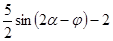 
.
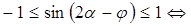
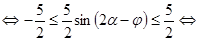
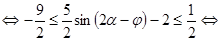
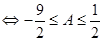Наименьшее значение выражения 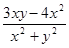равно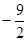 
. Значит, при 
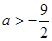неравенство имеет решение.
Ответ: при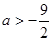 
неравенство имеет решение.
Алгебраическое решение
Если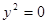 
, то неравенство примет вид
.
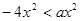Значит, при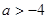 
неравенство имеет решение.
Поделим числитель и знаменатель на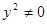 
, получим
.
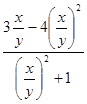Введем замену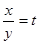 
, тогда
.
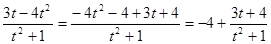Найдем наименьшее значение выражения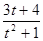 
.
.
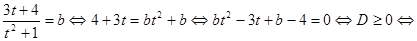
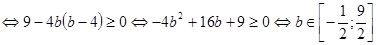То есть наименьшее значение выражения 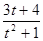равно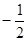 
. Тогда наименьшее значение выражения 
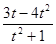, а значит наименьшее значение выражения 
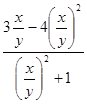равно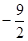 
.
Ответ: при 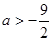неравенство имеет решение.
Для данного задания самый удобный метод решения – решение с помощью тригонометрической подстановки. Во втором случае возникает проблема с тем, чтобы найти наименьшее значение выражения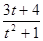 
. Если учащиеся умеют находить наименьшее значение функции с помощью производной, то выполнив все вычисления и проведя исследование, они справятся с задачей. Если подобное задание решать до изучения производной, то могут возникнуть трудности с определением наименьшего значения. В работе предложен прием сведения к уравнению с параметром, подробно описанный в предыдущем параграфе.
Глава 3
Дата: 2019-05-29, просмотров: 186.
