Диагностирующая контрольная работа была организована после проведения всех занятий, предусмотренных факультативом, и заняла 1 урок. Учащимся было предложено для обязательного решения 3 задачи и одно задание было вынесено на дополнительную оценку. При этом школьникам была предоставлена возможность самостоятельно выбрать метод решения каждой задачи. Цели контрольной работы:
1. Выявить степень усвоения учащимися материала.
2. Определить понимание необходимости обоснования введения тригонометрической подстановки.
3. Сравнить эффективность решения с помощью тригонометрической подстановки и без нее.
4. Выявить тот материал и те задания, которые вызывают наибольшие затруднения у учащихся.
План:
1. Организация учащихся на выполнение контрольной работы.
2. Выполнение работы по двум вариантам.
Содержание:
I Вариант
1. Решить уравнение 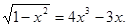
2. Найти наибольшее и наименьшее значения выражения 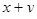 в области
в области 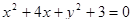 .
.
3. Среди всех решений (а, b, с, d) системы найти такие, при которых выражение а+с принимает наибольшее значение
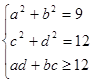 .
.
4. Сколько решений имеет уравнение в зависимости от параметра
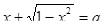 .
.
II Вариант
1. Решить уравнение 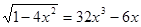 .
.
2. Найти наибольшее и наименьшее значения выражения 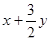 в области
в области 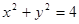 .
.
3. Среди всех решений (а, b, с, d) системы найти такие, при которых выражение а+с принимает наибольшее значение
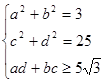 .
.
4. Сколько решений имеет уравнение в зависимости от параметра
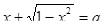 .
.
Оценивание: Правильно выполненное и аргументированное решение оценивалось знаком «+». Правильно выполненное решение с частичным обоснованием введения тригонометрической подстановки – знаком « 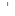 ». Правильно выполненное решение без обоснования применения тригонометрической подстановки, но с указанием промежутка изменения
». Правильно выполненное решение без обоснования применения тригонометрической подстановки, но с указанием промежутка изменения  – знаком «*». Правильно выполненное решение без обоснования применения тригонометрической подстановки и без указания промежутка изменения
– знаком «*». Правильно выполненное решение без обоснования применения тригонометрической подстановки и без указания промежутка изменения  – знаком «
– знаком « 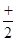 ». Решение с ошибками – знаком «
». Решение с ошибками – знаком « 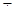 ». Отсутствие решения – знаком «–». Буква «д» рядом с одним из указанных выше знаков означает, что учащийся решал задание, не прибегая к тригонометрической подстановке. Буква «к» - учащийся в решении комбинирует тригонометрическую подстановку с другим способом решения. Буква «с» - учащийся представил два решения: с помощью тригонометрической подстановки и без нее.
». Отсутствие решения – знаком «–». Буква «д» рядом с одним из указанных выше знаков означает, что учащийся решал задание, не прибегая к тригонометрической подстановке. Буква «к» - учащийся в решении комбинирует тригонометрическую подстановку с другим способом решения. Буква «с» - учащийся представил два решения: с помощью тригонометрической подстановки и без нее.
Результаты: контрольная работа была написана 21 учеником класса из 22. Начнем с разбора обязательной части контрольной работы.
| Фамилия | 1 задание | 2 задание | 3 задание | |
| 1 | Бакулин | + | 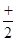
| 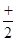
|
| 2 | Бизяев | 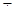
| 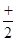
| 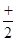
|
| 3 | Вахрушев | 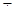
| 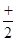
| 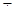
|
| 4 | Витвицкий | + | 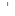
| +д |
| 5 | Громазин | + | 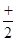
| 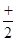 к к
|
| 6 | Давидюк | + | 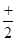
| 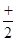
|
| 7 | Жичкина | + | + | * |
| 8 | Журавлев | + | 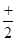
| 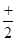
|
| 9 | Касьянов | + | 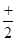
| 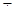
|
| 10 | Колупаева | 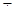
| 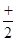
| * |
| 11 | Коновалов | 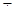
| 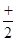
| 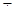
|
| 12 | Коробейников | 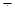
| + | +д |
| 13 | Макарова | + | 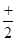
| 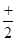
|
| 14 | Новоселов | + | 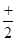
| * |
| 15 | Овчинников | 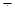
| 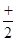
| 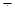
|
| 16 | Прокашев | + | 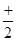
| 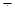
|
| 17 | Сероглазов | 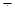
| * | * |
| 18 | Скачилова | + | 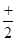
| 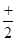
|
| 19 | Хохлов | 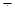
| 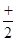
| 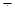
|
| 20 | Черняк | + | 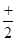
| +д |
| 21 | Шильников | 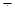
| 
| – |
| Процент учащихся, верно выполнивших задание | 57% | 100% | 67% | |
| Процент учащихся, выбравших тригонометрическую подстановку | 100% | 100% | 86% | |
| Процент учащихся, верно решивших с помощью тригонометрической подстановки[2] | 57% | 100% | 67% | |
| Процент учащихся, обосновавших введение тригонометрической подстановки | 100% | 14% | 22% | |
| Процент учащихся, верно решивших другим способом | – | – | 100% | |
Первое задание – решение иррационального уравнения – все учащиеся выполнили с помощью тригонометрической подстановки, причем во всех работах было представлено полное обоснование возможности введения этой подстановки. В восьми работах решение оказалось с ошибками. Все учащиеся, использовавшие подстановку 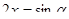 , где
, где 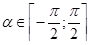 , допустили ошибки. Это было связано с тем, что в результате преобразований исходного уравнения в правой части получалась формула синуса тройного аргумента с отрицательным знаком, который был утерян. Потерю знака удалось избежать тем учащимся, которые выбрали подстановку
, допустили ошибки. Это было связано с тем, что в результате преобразований исходного уравнения в правой части получалась формула синуса тройного аргумента с отрицательным знаком, который был утерян. Потерю знака удалось избежать тем учащимся, которые выбрали подстановку 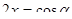 , где
, где 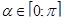 . Ошибки в решении при такой подстановке были связаны с неверным отбором корней.
. Ошибки в решении при такой подстановке были связаны с неверным отбором корней.
Второе и третье задания были посвящены нахождению наибольшего и наименьшего значений функции.
Второе задание всеми учащимися было решено верно, при этом в качестве метода решения был выбран метод тригонометрической подстановки. Но в отличие от решения первого задания, во втором только двое учащихся дали аргументированное решение с полным обоснованием возможности введения тригонометрической подстановки. В одной работе эта возможность не получила достаточно полного обоснования. Остальные восемнадцать учащихся приступили к решению без доказательства возможности введения замены, причем из них только один верно указал, что 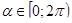 .
.
К решению третьего задания приступили двадцать учащихся из двадцати одного. Из них трое решали алгебраическим способом и полностью справились с решением. Один ученик начал решение алгебраическим способом, получил промежуточный результат, который использовал при решении с помощью тригонометрической подстановки, но все решение не было доведено до конца. Шестнадцать учащихся применили метод тригонометрической подстановки для решения, но ни в одной из этих работ не было обоснования введения этой подстановки, и только четверо указали, что 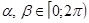 . Из шестнадцати работ шесть содержат ошибки. В трех решение было завершено после того, как было найдено наибольшее значение выражения, в то время как задание состояло в том, чтобы найти такие решения системы, при которых данное выражение принимает наибольшее значение. В остальных трех работах были допущены вычислительные ошибки.
. Из шестнадцати работ шесть содержат ошибки. В трех решение было завершено после того, как было найдено наибольшее значение выражения, в то время как задание состояло в том, чтобы найти такие решения системы, при которых данное выражение принимает наибольшее значение. В остальных трех работах были допущены вычислительные ошибки.
Перейдем к разбору дополнительного задания. Оно содержало уравнение с параметром, для которого требовалось исследовать количество решений в зависимости от параметра. Из двадцати одного ученика к заданию на дополнительную оценку приступили двадцать человек, из них половина верно справилась с ним. Семеро из верно решивших учащихся опирались на графическую иллюстрацию, трое – использовали алгебраический подход. Из не решивших десяти человек семеро привели исходное уравнение с помощью тригонометрической подстановки к виду 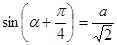 и продолжили решение для
и продолжили решение для 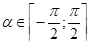 . Они не учли, что аргумент правой части равенства
. Они не учли, что аргумент правой части равенства 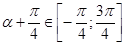 . Трое не рассмотрели все возможные случаи.
. Трое не рассмотрели все возможные случаи.
Дата: 2019-05-29, просмотров: 291.