Диференційований підхід у процесі навчання молодших школярів розв’язувати текстові задачі
Зміст
Вступ
Розділ І. Психолого-педагогічні основи диференційованого підходу в процесі вивчення математики учнями початкових класів
1.1 Враховування навчальних можливостей учнів як основа диференційованого підходу у навчанні
1.2 Характеристика основних видів диференційованого навчання
Розділ ІІ. Методика використання диференційованого підходу при навчанні учнів розв’язуванню текстових задач
2.1 Пошук шляхів вдосконалення методики формування вмінь молодших школярів розв’язувати текстові задачі
2.2 Організація і зміст експериментального дослідження
2.3 Аналіз ефективності експериментального дослідження
Висновки
Список використаної літератури
Додатки
Вступ
Проектом Державного стандарту загальної середньої освіти передбачається диференційоване навчання учнів початкових класів, а за мету курсу математики ставиться досягнення кожним учнем рівня навченості не нижче обов’язкового. Нові вимоги вимагають нових технологій навчання, які б забезпечили і високий рівень теоретичної та практичної підготовки з математики, і переорієнтацію навчально-виховного процесу на особистість учня, на сприятливі умови для досягнення кожним належного рівня знань, умінь і навичок.
Дані, необхідні для осмислення цілісності і цілеспрямованості формування вмінь розв’язувати текстові задачі в умовах диференційованого навчання, одержані нами в результаті аналізу психологічної і методичної літератури, де є немало цінних ідей і теоретичних узагальнень. Так, праці в галузі педагогічної психології (Л.С. Виготський, П.Я. Гальперін, Г.С. Костюк, О.М. Леонтьєв, Н.Ф. Тализіна, І.С. Якиманська) розкривають зміст поняття ”вміння” і розуміння механізмів його формування у школярів початкової школи. Психологічний та методичний аспект процесу розв’язування задач досліджували Г.О. Балл, Л.Л. Гурова, С.Д. Максименко, Є.І. Машбиць, Н.О. Менчинська, Н.А. Побірченко, З.І. Слєпкань, Л.М. Фрідман. Психолого-педагогічні і методичні основи диференційованого навчання розкрито в працях М.І. Бурди, Ю.З. Гільбуха, О.С. Дубинчук, С.О. Логачевської, О.Я. Савченко, І.Е. Унт та ін.
До проблеми розв’язування задач при вивченні математики тією чи іншою мірою зверталися відомі методисти. Особливу увагу розв’язуванню задач як засобу розвитку мислення, формування системи математичних понять, добору задач до підручників у середній школі приділяли Г.П. Бевз, Ю.М. Колягін, І.Ф. Тесленко, А.А. Столяр, Л.М. Фрідман, у початковій школі - М.О. Бантова, Г.В. Бельтюкова, М.В. Богданович, Г.В. Гап’юк, М.М. Левшин, М.Г. Моро, Я.А. Король, Л.П. Кочіна, А.С. Пчолко, Н. Уткіна та інші.
Як відомо, навчально-виховний процес повинен будуватися відповідно до потреб особистості та індивідуальних можливостей дітей, зростання їх самостійності й творчої активності. А це вимагає організації навчання відповідно до здібностей, здатності до навчання, таланту дитини [85,6].
Використання індивідуального підходу та диференційованих форм навчальної роботи зумовлюється і впливом гуманістичної тенденції у вихованні школярів. Як правило, «обраний учителем середній темп діяльності є нормальним лише для певної частини учнів, для інших він швидкий чи повільний. Одна і та ж учбова задача для одних дітей є складною, майже нерозв’язною проблемою, а для інших вона – легке питання. Один і той самий текст одні діти розуміють після першого читання, іншим необхідне повторення, а третім – пояснення» [63, 51].
Таким чином, успішність засвоєння навчального матеріалу, темп оволодіння ним, міцність збереження та рівень осмисленості знань залежать не лише від діяльності педагога, але й від пізнавальних можливостей і здібностей учнів, обумовлених багатьма чинниками: особливостями сприймання, пам’яті, мислительної діяльності, а також фізичним розвитком і т. ін. Тому «кожен учитель має створити такі умови, за яких стало б можливим використання фактичних і потенційних можливостей кожної дитини за класно-урочної форми навчання» [42, 11]. Розв’язання цього практичного завдання тісно пов’язане з послідовною реалізацією диференційованого та індивідуального підходу до школярів.
Рівень навчально-пізнавальної активності молодших школярів може істотно підвищитися за умови диференційованого підходу до організації навчально-виховного процесу [49,20].
Програму навчання математики в початковій школі побудовано так, щоб реалізувати багаті потенційні можливості дитини: перетворити її природну допитливість на стійкий пізнавальний інтерес, а жвавість, активність спрямувати в річище дослідницької діяльності [41,21].
Зміст диференційованого навчання вчитель визначає відповідно до змісту і конкретних завдань кожного уроку. З метою організації практичної діяльності учнів слід широко застосовувати індивідуальний роздатковий матеріал, диференційовані завдання на уроках математики [62,9].
Важливим аспектом методу диференційованого підходу вважається те, що учні самостійно вибирають зміст і обсяг роботи для себе. І ніхто не диктує, як працювати сьогодні. На кінець уроку у дитини є задоволення від зробленої роботи. У слабших учнів не виникає комплексу нижчевартості, вони починають вірити у власні сили.
Традиційна методика формування вмінь розв’язувати задачі орієнтована на «середнього» учня. Вона не враховує зміст та основні ідеї проекту Державного стандарту загальної середньої освіти в Україні, зокрема ідеї рівневої диференціації навчання й орієнтацію її результатів на можливості школярів в процесі навчання. Не всі підручники з математики для початкових класів спрямовані на диференційоване формування вмінь розв’язувати задачі. Окремі з них не мають навчального матеріалу для організації ефективної роботи різних за здібностями груп учнів.
Отже, вивчення психологічної, педагогіко-методичної літератури, аналіз досвіду вчителів-практикантів з проблеми диференційованого підходу до учнів у процесі навчання молодших школярів розв’язувати задачі підтверджують актуальність обраної теми дослідження, особливо в умовах переходу на нові програми і підручники. Виявлення шляхів удосконалення методики формування вмінь розв’язувати текстові задачі в умовах диференційованого навчання у початкових класах складає проблему нашого дослідження.
Об’єкт дослідження – процес навчання математики молодших школярів.
Предмет дослідження – формування вмінь учнів початкових класів розв’язувати текстові задачі в умовах диференційованого навчання.
Метою дипломної роботи є: розробити, теоретично обґрунтувати і експериментально перевірити добірку завдань для навчання розв’язувати текстові задачі в процесі диференційованої роботи.
Гіпотеза дослідження: якщо, навчаючи розв’язуванню текстових задач, враховувати зміст і операційний склад умінь, рівні програмових вимог їх формування, психолого-педагогічні засади вироблення вмінь, принципи добору знань, диференційованих за складністю, то це підвищить ефективність навчання учнів розв’язувати текстові задачі, а отже, рівень математичного розвитку школярів і підготовку їх в цілому.
Для реалізації мети дослідження необхідно роз’язати наступні завдання:
1) На основі аналізу психологічно-педагогічної і навчально-методичної літератури, практики навчання з’ясувати стан досліджуваної проблеми.
2) Узагальнити шляхи вдосконалення методики формування вмінь молодших школярів розв’язувати текстові задачі.
3) Розробити добірку завдань, диференційованих за складністю і спрямованих на вироблення вмінь розв’язувати текстові задачі в початковій школі.
4) Теоретично обґрунтувати та експериментально перевірити розроблену добірку диференційованих завдань для навчання учнів розв’язувати текстові задачі.
Під час написання дипломної роботи були використані такі методи педагогічного дослідження: аналіз наукової літератури; спостереження; бесіди; експеримент; узагальнення експериментальних даних.
Практичне значення дипломної роботи зумовлюється актуальними завданнями удосконалення навчально-виховного процесу та його важливого компонента – уроків математики. Окрім того, теоретично окреслено та практично втілено диференційований підхід при навчанні учнів розв’язуванню задач. Тому матеріали дослідження можуть бути використані учителями початкової школи та студентами факультету підготовки вчителів початкових класів.
Дипломна робота складається із вступу, двох розділів, списку використаної літератури.
Картка 1
1. Прочитай задачу.
2. Розглянь скорочений запис і повтори зміст задачі.
| Відстань за 1 год | Кількість годин | Загальна відстань | |
| Велосипедист Турист | 12 км ? | 2 6 | Однакова |
3. Користуючись схемою, склади до задачі вираз і розв’яжи його.
1 · 1 : 1
4.
5. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Склади план розв’язування і розв’яжи її.
3. Запиши відповідь.
4. З’ясуй додатково, за скільки годин велосипедист проїде 84 км.
Картка 3
1. Прочитай задачу.
2. Розв’яжи задачу, склавши вираз.
3. Запиши відповідь.
Додаткове завдання
1. Зміни запитання задачі так, щоб вона розв’язалася трьома діями.
2. Обчислення і відповідь запиши.
Для постановки завдань за підручником вчитель роздає дітям кружечки різного кольору: першій групі – червоні, другій – рожеві, третій – зелені. Відповідно на дошці подається такий запис:
Картка 1 – рожевий, Картка 2 - зелений, Картка 3 – червоний.
Вказівки про повторну роботу над задачами вчитель подає усно. У ході перевірки правильності виконання завдань слід розглянути всі варіанти.
Диференційовано-групова форма організації роботи сприяє підвищенню інтересу до навчальної діяльності, розвитку працездатності, але треба враховувати і можливість негативного її прояву. Учні не повинні знати про поділ їх на різні групи. Вчитель повідомляє, що робота за картками проводиться для того щоб кожен мав можливість працювати самостійно. Він не вказує, що в тій чи іншій групі завдання більш важкі. Треба виключити можливість прояву зазнайства з боку сильніших учнів і всебічно заохочувати слабших.
З наведеного видно, що форми організації навчальної діяльності учнів можуть бути різні. У кожному випадку необхідно вибирати оптимальну з урахуванням поставленої навчальної мети.
ІІ етап
І в. Самостійно запиши в зошитах розв’язок задачі за допомогою дій з поясненням.
В магазин привезли 7 ящиків яблук по 6 кг у кожному і 5 ящиків груш по 7 кг у кожному. Скільки кілограмів фруктів привезли до магазину?
ІІ в. Аналіз подібної задачі (змінено тільки числові дані, щоб полегшити сприймання сюжету задачі). Розв’язок запиши з коментуванням.
Задача
| Назва продукту | Маса 1 ящика | Кількість ящиків |
| Яблука груші | 7 4 | 9 8 |
Слухають усі. Перевірка всіх завдань.
ІІІ етап
І в. Самостійно розв’яжи задачу (змінено сюжет і числові дані).
У магазин привезли іграшки в пакетах: 80 кубиків по 10 штук у пакеті і 50 м’ячів по 5 у пакеті. Скільки всього пакетів з іграшками привезли в магазин?
ІІ в. Фронтальна робота. Аналіз подібної задачі (змінено сюжет попередньої задачі) і самостійний запис розв’язування.
Для вчителів побудували 8 будинків по 3 квартири і 7 будинків по 10 квартир. Скільки всього квартир побудували для вчителів?
Слухають усі. Перевірка всіх завдань.
IV етап
І в. Склади задачу за схемою і запитанням (можна запропонувати таблицю «Магазин»).
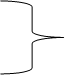1 по 1
?
1 по 1
Скільки грошей заплатила господиня?
ІІ в. Самостійно розв’яжи подібну задачу (змінено сюжет і числові дані).
Школярі у саду посадили 4 ряди яблунь по 7 дерев у кожному ряду, а груш - 3 ряди по 8 дерев у кожному. Скільки всього дерев посадили школярі?
Слухають усі. Перевірка всіх завдань.
Аналогічно можна побудувати роботу з опрацювання будь-якого виду задачі.
Готуючись до уроку, вчитель визначає не тільки навчально-пізнавальну мету, а й способи її досягнення, що здійснюється на основі поєднання фронтальної, індивідуально-групової та індивідуальної роботи. Велике значення при цьому мають диференційовані завдання, які сприяють розвитку знань одних учнів, у надолуженню не опанованих ще знань інших учнів. У вчителя початкових класів на уроки математики для кожної теми чи виду роботи має бути розроблена добірка завдань, диференційованих за складністю і спрямованих на вироблення вмінь розв’язувати текстові задачі.
В умовах класно-урочного навчання школярі з різними здібностями ознайомлюються з новим матеріалом одночасно. Тому для здійснення диференційованого підходу в навчанні молодших школярів розв’язувати текстові задачі здебільшого добирають завдання, які мають спільну пізнавальну мету, але відрізняються ступенем трудності чи мірою допомоги.
Здійснюючи принцип диференційованого підходу, вчитель має бути тактовним, спиратися на позитивні якості дитини. Не слід оперувати словами сильні учні, слабкі учні. Краще відзначати ступінь просування дітей в опануванні вмінь, самостійність, оригінальність розв’язування тощо.
Організовуючи самостійну роботу учнів над задачами, найчастіше застосовують такі три види диференціації: індивідуалізація вимог до спільного завдання; спрощення одного з двох варіантів самостійної роботи; надання допомоги в одному з варіантів самостійної роботи (індивідуальна допомога) [8,87].
1) Індивідуалізація вимог до спільного завдання. Для всіх учнів записується на дошці чи вказується в підручнику єдине завдання, але інструкція його виконання передбачає й деякі прийоми диференціації.
Урізноманітнення вимоги до розв’язання текстових задач. Всім учням пропонується та сама задача, причому одразу дається й додаткове завдання щодо цієї задачі. Такими додатковими завданнями можуть бути: розв’язати задачу іншим способом, скласти числовий вираз за розв’язанням задачі окремими діями, змінити запитання і знайти на нього відповідь, скласти подібну задачу, скласти і розв’язати обернену задачу (3 клас), записати план розв’язання задачі (4 клас).
Постановка кількох запитань до умови задачі. Вчитель записує умову задачі і до неї 2-3 запитання. Кожен учень знаходить відповіді на стільки запитань, на скільки зможе. Зрозуміло, що бажано відповісти на всі запитання.
Задача № 976 (3 клас)
Дві кравчині мають пошити по 96 сорочок. Одна з них шиє за день 12 сорочок, а друга - 16.
Запитання. 1) За скільки днів пошиє перша кравчиня 96 сорочок?
2) За скільки днів пошиє друга кравчиня 96 сорочок?
3) Яка кравчиня виконує роботу раніше і на скільки днів?
Учитель. Уважно прочитайте умову задачі. Запишіть скорочено умову в зошит. Дайте відповідь на перше запитання, а хто зможе і встигне, то й на друге і третє.
Завдання з трьома задачами. Вчитель записує на дошці 3 задачі, які мають певну схожість, але різні за ступенем складності. Перша задача є підготовчою до другої.
Спочатку дітям пропонується розв’язати другу задачу. Коли частина класу виконає завдання, вчитель дає таку вказівку: «Учні, які розв’язали другу задачу, починають розв’язувати третю задачу. Хто не зміг розв’язати другу задачу, хай спробує розв’язати першу.
2) Спрощення одного з варіантів самостійної роботи. Завдання для самостійної роботи готують у двох однакових за навчальною метою варіантах. Проте в одному варіанті дається легша задача. Це може бути задача, яку вже розв’язували в класі, або аналогічна, де змінено числові значення. Числові дані добираються так, щоб прийоми виконання дій над ними були вже добре засвоєні, оскільки учні повинні зосереджувати увагу не на обчисленні, а на зв’язках між величинами. Наведемо зразок такої роботи.
Варіант 1.
Задача № 388 (3 клас)
У 6 однакових ящиках 30 кг лимонів. Яка маса лимонів у 4 таких ящиках?
Другий (полегшений) варіант полягає в тому, що учень виконуватиме дії над одноцифровими та круглими цифрами (10 : 5 = 2, 2 · 3 = 6), тим часом як основний (перший) передбачає ділення іменованого числа на двоцифрове, множення на двоцифрове або трицифрове число.
Варіант 2
Задача.
За 5 партами сидить 10 учнів. Скільки учнів сидить за 3 партами?
Диференційовані завдання при розв’язуванні задач випливають з тих чи інших несформованих вмінь і навичок. Це може бути:
1) диференціація за ступенем складності (індивідуалізація вимог до загального завдання):
ü на які запитання можна ще дати відповідь, користуючись умовою задачі, запишіть їх і дайте на них відповідь;
ü складіть задачу, обернену даній і розв’яжіть її;
ü складіть вираз до задачі;
ü складіть за одержаним виразом свою задачу.
Індивідуальна допомога. Завдання для самостійної роботи пропонується у 2 - 4 варіантах. В одному чи двох з них міститься додаткова інформація, розрахована на допомогу в розв’язуванні задач. Реалізується цей вид диференціації через індивідуальні картки.
2) Диференціація за ступенем допомоги:
ü додаткові запитання;
ü додаткові вказівки;
ü додаткова конкретизація (короткий запис змісту задачі);
ü вибір правильного розв’язування;
ü виконання деякої частини завдання;
ü додаткові вправи.
3) Розв’язування задач за готовим планом
Групова форма
Групи учнів не постійні, їх кількісний і якісний склад може здійснюватися залежно від рівня досягнень учнів, змісту теми тощо. Об’єднуючи учнів у групи, вчитель одержує можливість організувати навчання різне за змістом, рівнем складності, обсягом завдань, тобто враховує індивідуальні запити школярів за певних умов.
При диференціації учителю необхідно:
- враховувати загальну готовність учнів до наступної діяльності;
- передбачати труднощі, які можуть виникнути в учнів під час засвоєння матеріалу;
- використовувати диференційовані завдання індивідуального та групового характеру в системі уроків;
- проводити перспективний аналіз діяльності власної і учнів: з якою метою планується виконання тих чи інших завдань, чому їх треба виконувати саме на даному етапі уроку, як продовжити розпочату роботу на наступних уроках.
а) Парна
1. Поставити один одному такі запитання:
- Що в задачі відомо про …?
- Що запитується в задачі?
- Скількома діями можна розв’язати задачу?
Мета: розвиток умінь опрацювати зміст задачі.
2. Перевірити один одного, чи правильно зрозумів задачу, а потім удвох обміркувати план її розв’язання.
Один учень називає запитання плану, а другий – дії, що треба виконати.
Мета: розвиток умінь знаходити і обговорювати план розв’язання задачі.
3. Розв’язати задачу самостійно, а потім зробити взаємоперевірку.
Мета: розвиток умінь контролювати правильність ходу розв’язання задачі.
б) Ланкова (діяльність постійних груп учнів) тривалість роботи 5 – 10 хвилин протягом уроку.
1) 4 задачі різного типу. Кожен учень бере задачу, яку дає ланковий, витягнувши з конверта.
2) Задачі для ланок дублюються.
3) Для однієї ланки лише 2 задачі.
4) Для однієї ланки 1 задача. Кожна ланка має задачі різного типу.
в) Диференційовано-групова. 3 групи – сильніша, середня і слабка. Для слабкої групи дається підказка.
Отже, готуючи диференційовані завдання, вчитель обов’язково зіставляє їх мету й зміст з рівнем знань і розвитку учнів, шукає те спільне в змісті й характері завдань, без чого не можна правильно визначити ступінь їх складності для кожної групи, і на цій основі визначає необхідний і посильний зміст та обсяг роботи. Лише за таких умов створюються сприятливі можливості для успішного навчання кожної дитини.
Задача.
Якщо шматок дроту розрізати на 4 частини по 16 м у кожній, то залишиться ще 6 м. однак дріт розрізали на частини по 5 м у кожній. На скільки частин розрізали дріт?
Аналіз. Щоб знайти відповідь, треба знайти довжину всього шматка дроту. Знайдемо довжину за першою частиною умови. Залишилося 6 м. отже, потрібно ще знайти, скільки метрів дроту розрізали на 4 частини.
Закінчи аналіз задачі, склади план її розв’язування і запиши розв’язання. Зразок розв’язування. На картці подано дві задачі одного виду, одна з яких вже розв’язана.
1. Доярка надоїла 9 л молока. 16 л вона віддала телятам, а решту розлила порівну в 4 бідони. Скільки літрів молока доярка налила в один бідон?
1) 96 – 16 = 80 (л);
2) 80 : 4 = 20 (л).
Відповідь. 20 літрів.
2. Виготовили 40 л томатного соку. 13 л соку вилили в сулію, а решту розлили порівну в 9 банок. Скільки літрів соку налили в одну банку?
Перевірити розв’язання першої задачі та розв’язати другу. Подання пояснення чи плану розв’язання задачі.
Інколи учителю важко було скласти картку з допомогою, особливо коли ця допомога була диференційованою. В цьому випадку до однієї і тієї ж задачі потрібно було зробити 3 картки. Одну дати сильному учневі, другу дати середньому, а третю – слабкому учневі.
Наведемо приклад диференціації на трьох картках.
Картка 1
1. Прочитай задачу.
2. Розглянь графічний малюнок до неї.
 |
3. Розв’яжи задачу, добираючи відповідні дії.
1) _____________________ - пролетів літак за 3 год;
2) _____________________ - пролетів літак за 2 год;
3) _____________________ - всього пролетів літак;
4) _____________________ - залишилося пролетіти.
4. Запиши відповідь і зроби перевірку за схемою.
1 + 1 + 1 = 4500 (км)
Картка 2
1. Прочитай задачу.
2. Склади план і розв’яжи задачу.
3. Запиши відповідь.
Картка 3
1. Прочитай задачу.
2. Склади числовий вираз і розв’яжи задачу.
3. Запиши відповідь.
Додаткове завдання
1. Обчисли, на скільки менше відстані залишилося пролетіти, ніж він пролетів.
2. Запиши відповідь
У ході експерименту порівняння ефективності навчання в експериментальному та контрольному класах здійснювалося за такими показниками:
1) за результатами засвоєння основного матеріалу програми з математики для початкових класів;
2) за змінами в загальному розвитку дітей, їхніх інтересах, ставленні до навчання.
У квітні місяці в експериментальному і контрольному класах були проведені контрольні роботи. Перше, друге та третє завдання стосувалося суто програмового матеріалу, четверте не виходило за межі програми, але мало певні ускладнення у формулюванні.
Наведемо приклади цього завдання і результати його виконання.
? Розв’яжи задачу за допомогою рівняння.
У магазин привезли 154 пари взуття. Через п’ять днів залишилося 87 пар. Скільки пар взуття продали протягом п’яти днів?
Виконання підсумкових програмових завдань (квітень)
В експериментальному і контрольному класах
| Правильно розв’язали (у відсотках) | ||
| Класи | 1- 2 е завдання | 3-е завдання |
| 4-б контрольний | 76 | 77 |
| 4-а експерим. | 80 | 83 |
Виконання додаткових завдань в експериментальному
і контрольному класах
| Правильно розв’язали (у відсотках) | |
| Класи | 4-е завдання |
| 4-б контрольний | 77 |
| 4-а експерим. | 82 |
Порівняння наслідків виконання контрольної роботи свідчить про те, що в експериментальному класі рівень умінь розв’язувати текстові задачі, застосовуючи диференційований підхід, значно вищий, ніж у контрольному, причому особливо відрізняються результати розв’язання додаткового завдання. Ми пояснюємо це цілеспрямованою роботою диференційованого підходу у процесі навчання молодших школярів розв’язувати текстові задачі, яка проводилася відповідно до завдань формуючого експерименту, що привело до позитивних зрушень у розвитку мислення школярів.
Діаграма
Висновки
Проведене експериментальне дослідження, присвячене диференційованому підходу у процесі навчання молодших школярів розв’язувати текстові задачі дозволило розв’язати поставлені задачі і сформулювати основні результати дослідження.
Вивчаючи стан досліджуваної проблеми в психолог-педагогічній та навчально-методичній літературі, практиці навчання ми прийшли до таких висновків.
- Потреби сучасного суспільства вимагають вже в молодшому шкільному віці рівня сформованості розв’язувати текстові задачі, застосовуючи диференційований підхід.
- Проведений аналіз наукових розробок, навчальної та методичної літератури, роботи вчителів-класоводів засвідчує, що і в теорії, і в практиці школи проблема диференційованого підходу при розв’язуванні текстових задач має певне відображення. Проте на сьогодні немає цілісного підходу вирішення цієї проблеми, хоч присутні зразки диференційованих завдань і є методика використання диференційованого підходу при навчанні учнів розв’язувати текстові задачі.
Диференційований підхід до учнів початкових класів з врахуванням типових особливостей їх учбової діяльності дає змогу ширше використовувати і виховні можливості уроку. Навчання зможе повніше виконати свою виховну функцію, якщо на кожному уроці, при роботі з будь-яким навчальним матеріалом вчителі будуть формувати певні властивості особистості учня залежно від його індивідуально-типологічної приналежності.
Диференційоване навчання – це один із способів досягнення всіма дітьми загальноосвітньої мети навчання з урахуванням їх індивідуальних особливостей
Диференційований підхід має пронизувати весь навчальний процес. Плануючи диференційовані завдання, вчитель обов’язково повинен зіставляти їх мету і зміст з рівнем знань і розвитку учнів, шукати спільне в змісті й характері завдань, без чого не можна правильно визначити для кожної групи ступінь складності, необхідний і посильний об’єм роботи. Лише за цих обставин створюються сприятливі умови для найповнішого розвитку здібностей, вміння і бажання вчитися.
У процесі використання диференційованих завдань здійснюється поступовий перехід від колективних форм роботи учнів до частково самостійних і повністю самостійних у межах уроку або системи уроків. Такий підхід дає можливість учням брати участь у виконанні завдань, складність яких зростає.
Узагальнення власних напрацювань і досвіду інших дає змогу виділити сукупність педагогічних вимог до роботи вчителя, за яких навчання на різних рівнях стає ефективним. Учителю необхідно:
1) враховувати загальну готовність учнів до наступної діяльності;
2) передбачати труднощі, які можуть виникнути в учнів під час засвоєння матеріалу;
3) використовувати диференційовані завдання індивідуального та групового характеру в системі уроків;
4) проводити перспективний аналіз діяльності власної та учнів: з якою метою планується виконання тих чи інших завдань, чому їх треба виконувати саме на даному етапі уроку, як продовжити розпочату роботу на наступних уроках.
Педагогічний експеримент був пов’язаний із формуванням у молодших школярів вмінь розв’язувати текстові задачі при диференційованому підході. Ми пропонували четвертокласникам добірку завдань, диференційованих за складністю і спрямованих на вироблення в учнів вмінь розв’язувати текстові задачі. У процесі експериментального дослідження навчання учнів розв’язувати задачі на уроці організовувалося у формі колективної фронтальної або індивідуальної самостійної роботи, а також групової форми навчання. Організовуючи самостійну роботу учнів, найчастіше застосовувалися три види диференціації: індивідуалізацію вимог до спільного завдання; індивідуальна допомога; спрощення одного з двох варіантів самостійної роботи. Початкове ознайомлення учнів з текстовими задачами проводилося у фронтальній формі. Групова робота у нашому дослідженні здебільшого застосовувалася у формі диференційовано-групової роботи. Над диференційованими завданнями індивідуально працювали сильні учні. Важливе значення в організації діяльності учнів під час індивідуальної роботи мали способи допомоги.. Найбільший вплив на розвиток математичних здібностей школярів мали вправи логічного змісту, комбінаторні, з елементами дослідження та завдання на кмітливість. Виявлення ефективності розробленої добірки диференційованих завдань у формуванні математичних уявлень і понять у молодших школярів ми здійснювали на основі порівняння сформованості відповідних навичок та вмінь в учнів експериментального класу порівняно з контрольним. Отримані результати формуючого експерименту підтвердили гіпотезу, що при навчанні розв’язувати текстові задачі потрібно враховувати зміст і операційний склад умінь, рівні програмових вимог їх формування, психолого-педагогічні засади вироблення відповідних вмінь. Принципи добору завдань, диференційованих за складністю, позитивно вплинули на формування відповідних уявлень і понять в учнів експериментального класу, що свідчить про ефективність застосовуваного напрямку роботи.
Використана література
1. Актуальне проблемы дифференцированого обучении / Под. ред. Рожиной Л.Н. Минск.: Народная АСВЕТА, 1992. – 191 с.
2. Бантова М.О., Бельтюкова Г.В., Полевщикова О.М. Методика викладання математики в початкових класах. - К.: Вища школа, 1977. – 288 с.
3. Баранов С.П. Сущность процесса обучения. - М.: Просвещение, 1981. - 144 с.
4. Баринова О.В. Дифференцированное обучение решению математических задач // Начальная школа. - 1999. - № 2. - С.41-45.
5. Богданович М.В. Диференційовані завдання з математики для 3 класу. - К.: Радянська школа, 1984. – 112 с.
6. Богданович М.В. Математика. Підручник для 3класу. – Київ: Освіта, 2003. – 224 с.
7. Богданович М.В. Математика. Підручник для 4 класу. – Київ. Освіта, 2004. – 159 с.
8. Богданович М.В. Методика розв’язування задач у початковій колі. - К.: Вища школа, 1990. - 183 с.
9. Богданович М.В. Урок математики в початковій школі. - К.: Радянська школа, 1990. – 192 с.
10. Богданович М.В., Козак М.В., Король Я.А. Методика викладання математики в початкових класах. – Тернопіль: Богдан, 2006. – 336 с.
11. Бондар В. Дидактика. - К.: Либідь, 2005. - 264 с.
12. Братанич О. Реалізація диференційованого навчання в умовах комбінованого уроку // Рідна школа. - 2000. - № 11- С.49-52.
13. Бурчин М.С. Инновации и новизна в педагогике // Советская педагогика. -1989. - № 12. - С. 36-40.
14. Бутузов И.Т. Дифференцированное обучение – важное дидактическое средство эффективного обучения школьников. – М.: Педагогика, 1978. – 200 с.
15. Вихрущ В.О. Теоретичні основи та актуальні проблеми сучасної дидактики. - Тернопіль: Ліком, 1997.
16. Волков К.Н. Психологи о педагогических проблемах. - М.: Просвещение, 1981. - 128 с.
17. Володько В.М. Індивідуалізація й диференціація навчання: понятійно-категорійний аналіз // Педагогіка і психологія. – 1997. - № 4. - С.9-17.
18. Выготский Л.С. Педагогическая психология / Под. ред. Давыдова В.В. - М.: Педагогіка, 1991. - 480 с.
19. Глушков И.К. Дифференцированная работа над задачами // Начальная школа. – 1986. - № 2. - С.34-35.
20. Глушков И.К. Изучение нового материала с использованием дифференцированных заданий // Начальная школа. – 1992 - №4. - С.29-33.
21. Головне управління шкіл. Про досвід роботи С.П.Логачевської // Початкова школа. - 1987. - № 12. - С.31-32.
22. Гончаренко С. Український педагогічний словник. - Київ: Либідь, 1997.- 376 с.
23. Гора Т.П., Грушина Т.В., Логачевська С.П. Диференціація навчання на уроках математики в 1 класі // Початкова школа. - 1994. - № 12. - С.24-31.
24. Гора Т.М., Мельничук Т.Й., Логачевська С.П. Таблиці з диференційованими завданнями з математики для 1-2 класів чотирирічної школи // Початкова школа. - 1993. - № 8. - С. 24-32.
25. Гора Т.П., Логачевська С.П. Диференційований підхід до розв’язування текстових задач // Початкова школа. - 1998. - № 1. - С.17- 22.
26. Гусак П.М. Теорія і технологія диференційованого навчання майбутніх вчителів початкових класів.: Автореферат. Дисертація доктора педагогічних наук. – К. – 1999. – 37 с.
27. Гюнтер Клаус. Введение в дифференциальную психологию учения. - М.: Педагогика, 1987. - 176с.
28. Деменева Н.Н. Дифференцированная работа на уроках математики в начальной школе // Начальная школа. - 2004. - № 2. - С. 55-61.
29. Дівакова І.І. Інтерактивні технології навчання у початкових класах. -Тернопіль.: Мандрівець, 2007. - 180 с.
30. Дифференциация в начальном звене / Под. ред. Ю.З. Гильбуха. - К.: НПЦ. Перспектива, 1996. – 54 с.
31. Диференціація навчання учнів у загальноосвітній школі. Методичній рекомендації. – Київ: Освіта, 1992. – 32 с.
32. Дорофеев Г.В., Кузнєцова Л.В. Дифференциация в обучении математике. // Математика в школе. - 1990. - № 4. – С.15- 21.
33. Дудко Л.М., Московченко В.М. Диференційована робота над задачами // Початкова школа. – 1994. - № 3. - С.16-17.
34. Елабугина-Полежаева Н.А. Дифференцированный поход при выполнении домашнего задания по математике // Начальная школа. - 1990. - № 1. -С.31-33.
35. Завізєна Н. Тлумачення індивідуального навчання в психолого-педагогічній літературі // Рідна школа. - 1999. - № 9. - С.55-57.
36. Загальна Психологія. Навчальний посібник З = 14 / За ред. О.Скрипченко, Л. Волинська, З. Огороднійчук та ін. – К.: А.П.Н., 1999. – 463 с.
37. Закон України про освіту.
38. Закон України про Загальну Середню школу.
39. Запереченко Н. Диференційований підхід до навчання // Початкова школа. – 2000. - № 2. - С.5-7.
40. Запереченко Н. Диференційований підхід до навчання // Початкова школа. - 2000. - № 5. - С.10-12.
41. Захарова А.М. Розвивальне навчання математики в початковій школі // Педагогіка і психологія. - 2000. - № 1. - С.21-23.
42. Зимняя О.А.Педагогическая психология. - М.: Просвещение, 1999. – 476 с.
43. Іванішена С. Форми і методи інтерактивного навчання // Початкова школа. - 2006. - № 3. – С. 9-11.
44. Казанський Н.Г., Назарова Т.С. Дидактика (начальные классы). - М.: Просвещение, 1978. - 224 с.
45. Калініченко Н. Малюків навчає кандидат наук // Початкова школа. - 2007. - № 1. – С.59-60.
46. Капиносов А.Н. Уровневая дифференциация при обучении математике в V – IX класах // Математика в школе. - 1990. - № 5. – С.16-19.
47. Каткова Э.Н. Дифференцированные задания при работе над ошибками в решении задач // Начальная школа. - 1985. - № 10. - С.40-42.
48. Коберник Г.І. Диференційоване навчання на уроках математики // Початкова школа. - 1999. - № 9. - С.25-27.
49. Коберник Г.І. Стимулювання навчально-пізнавальної активності молодших школярів в умовах диференційованого навчання (на матеріалах уроків математики).: Автореферат. Дисертація кандидата педагогічних наук. – К., 1995. – 23 с.
50. Коваль К. Підготовка майбутнього вчителя початкової школи до моделювання уроків за різними навчальними технологіями // Початкова школа. - 2005. - № 11. - С. 22-26.
51. Коваль Л.В. Диференціювання домашніх завдань з математики // Початкова школа. - 1991. - № 7. - С28-31.
52. Когут О.І. Інноваційні технології навчання української мови і літератури. -Тернопіль: Астон, 2005. – 203 с.
53. Комар О. Навчання школярів за інтерактивними методами // Рідна школа. – 2006. - №5. - С.57- 60.
54. Концепція загальної середньої освіти. (12 – річна школа).
55. Корсакова О. Про технологію диференційованого навчання // Рідна школа. - 2001. - № 9. - С.44-46.
56. Корчевська О.П. Навчання молодших школярів розв’язувати математичні задачі підвищеної складності: Дисертація на здобуття наукового ступеня кандидата педагогічних наук. – Тернопіль, 2000. – 222 с.
57. Корчевська О.П., Козак М.В. Робота над математичними задачами в 4 класі. -Тернопіль.: Астон, 2002. – 204 с.
58. Корчевська О., Кордуба Н. Диференційовані контрольні роботи з математики. – Тернопіль: Підручники і посібники, 2007. – 32 с.
59. Косенко О. Диференціація на уроках навчання грамоти // Початкова освіта. - 2008. - № 6. - С.17-19.
60. Костогриз С. Використання опорних схем і таблиць на уроках математики // Початкова школа. - 2004. - № 5.
61. Кочина Л., Листопад Н., Шпакова В. Математика (30 занять) // Початкова школа. - 2001. - № 7. - С.49-61.
62. Кочина Л.П. Навчання математики в підготовчих класах. - К.: Радянська школа, 1982. - 152 с.
63. Кравець Н.П. Організація роботи груп учнів в умовах внутрішньо- класного диференційованого навчання // Початкова школа. – 1993. - № 5-6. - С.49-51.
64. Кубрак В.І. Організація та керівництво диференційованим навчанням // Початкова школа. - 1991. - № 4. - С.52- 55.
65. Кубрак В.І., Дроб’язко П.І. Диференційоване навчання в початкових класах // Педагогіка і психологія. - 1994. - № 2. - С.71-76.
66. Латохіна Л.Г. Класифікація диференційованих завдань для самостійної роботи з математики. // Початкова школа. - 1984. - № 9. - С.44.
67. Логачевська С.П. Використання матеріалу підручника для диференційованих завдань // Початкова школа. – 1990. - № 8. – С.33-38.
68. Логачевська С.П. Диференційовані домашні завдання з математики // Початкова школа. - 2003. - № 7. - С.18-21.
69. Логачевська С.П. Диференціація на уроках математики // Початкова школа. - 1999. - № 7. - С.26 – 28.
70. Логачевська С.П. Диференційоване навчання на уроках математики // Початкова школа. - 2001. - № 5. - С. 18-22.
71. Логачевська С.П. Диференційований підхід до навчання // Початкова школа. - 1987. - № 5. - С.33-36.
72. Логачевська С.П. Диференціація – одна із форм інтерактивного навчання молодших школярів // Початкова школа. – 2006. - №10. - С.18 – 23.
73. Логачевська С.П. Диференціація у звичайному класі. – Київ: Заповіт, 1998.
74. Логачевська С.П. Дійти до кожного учня. - Київ: Радянська школа, 1990. – 158 с.
75. Логачевська С.П. Індивідуалізація завдань для шестиліток // Початкова школа. - 1990. - № 2. - С.27-30.
76. Логачевська С.П. Методичні рекомендації до посібника «Вчимося розв’язувати задачі» // Початкова школа. - 2003. - № 10. - С.15-17.
77. Логачевська С.П. Тренувальні вправи з математики // Початкова школа. - 1999. - №12. - С.22-26.
78. Логачевська С.П., Каганець Т. Індивідуалізація завдань на етапі закріплення з математики // Початкова школа. - 1998. - № 4. – С.17-20.
79. Логачевська С.П., Каганець Т. Індивідуалізація завдань на етапі закріплення знань з математики // Початкова школа. –1998.- № 5. С. 16-20.
80. Максименко С.Д. Загальна психологія. -Вінниця.: Нова книга, 2004. -702 с.
81. Маланюк К.П. Диференційований підхід до розв’язування текстових задач // Початкова школа. – 1989. - № 4. - С.19-23.
82. Мельничук Т.Й., Гора Т.П., Логачевська С.П. Прийоми і способи диференціації на уроках математики в межах одного класу // Початкова школа. - 1993. - № 1. - С.20-24.
83. Мізюк В.А. Диференціювання завдань при розв’язуванні текстових задач // Початкова школа. - 1996. - № 12. С.21- 23.
84. Мізюк В.А. Диференційований підхід до вивчення математики // Початкова школа. - 1997. № 12. – С.33-34.
85. Мізюк В.А. Формування вмінь учнів початкової школи розв’язувати текстові задачі. Автореферат дисертації на здобуття наукового ступеня кандидата пед. наук. – Київ: 2000. – 20 с.
86. Могилевська С.В. Диференціація самостійних завдань // Початкова школа. - 1984. - № 1. - С.50-53.
87. Мойсеюк Н.Є. - Педагогіка. К.: ВАТ «КДНК», 2001. – 608 с.
88. Московченко В., Дудко Л., Московченко В. системний підхід до розв’язування задач на продуктивність і спільну роботу // Початкова школа. - 1998. - № 5. - С.20-22.
89. Моро М.Г., Пишкало А.М. Методика навчання математики в 1-3 класах. -К.: Радянська школа, 1979. – 316 с.
90. Моро М.И., Степанова С.В. Уроки математики в эксперементальном подготовленом классе // Начальная школа. - 1985. - № 2. - С.25-30.
91. Оконь В. Основы проблемного обучения. - М.: Просвещение, 1968.– 208 с.
92. Освітні технології. Навчально-методичний посібник / За ред. Пєхоти О.М. – Київ: А.С.К., 2001. – 256 с.
93. Осмаловская М.М. Организация дифференцированного обучения в современной общеобразовательной школе. – М. – Воронеж, 2005. – 216 с.
94. Падалка О.С., Нісімчук А.М., Смолюк І.О., Шпак О.Г. Педагогічні технології. Навчальний посібник для вузів. – Київ: Українська енциклопедія ім. М.П.Бажана, 1995.
95. Педагогіка. Большая современная энциклопедия / Под. ред. Рапацевич Е.С. – Минск: Современное слово, 2005.
96. Перлини досвіду. Збірник методичних знахідок учителів початкових класів / Упор. Н. Гордіюк – Тернопіль: Мандрівець, 2007. – 112 с.
97. Підвищення ефективності початкового навчання / Під. ред. Скрипченко О.В., Савченко О.Я. - К.: Радянська школа, 1974. - 144 с.
98. Побірченко Н., Коберник Г. Інтерактивне навчання в системі нових освітніх технологій // Початкова школа. - 2004. - № 4. - С.8-10.
99. Побірченко Н. Інтерактивне навчання в системі нових освітніх технологій // Початкова школа. - 2004. № 10.
100. Покровская С. Е. Дифференцированное обучение учащихся в средних общеобразовательных школах. – Минск: Белоруская навука, 2002. – 319 с.
101. Програми для середньої загальноосвітньої школи 1- 4 класи. - К.: Початкова школа, 2006. – 432 с.
102. Розв’язування математичних задач у початкових класах / За ред. Т.М. Хмари. - К.: Радянська школа, 1986. - 96 с.
103. Рыбников К.А. К вопросу о дифференциации обучении // Математика в школе. - 1988. - № 5. – С.35.
104. Савченко О.Я. Дидактика початкової школи. - К.: Ґенеза, 1999. – 368 с.
105. Савчин М.В. Педагогічна психологія. - К.: Академвидав, 2007. - 424 с.
106. Святченко О. Диференціація – умова успішного навчання // Початкова освіта. - 2007. - № 12. - С.2-4.
107. Семенова А.В., Гурін Р.С., Осипова Т.Ю. Основи психології і педагогіки. Навчальний посібник. - К.: Знання, 2006. - 320 с.
108. Семенов Е.Е., Малиновський В.В. Дифференцированное обучение математике с позиций гуманизма // Математика в школе. -1991. - № 6. С.3-6.
109. Селевко Г.К. Энциклопедия образовательных технологий: В 2 – х т.т. – М.: НИИ школьных технологий, 2006. – Т.1. – 816 с.
110. Сікорський П.І. Теоретико-методичні основи диференційованого навчання. – Львів: Каменяр, 1998. – 196 с.
111. Сісецький П.В., Коберник Г.І. Основи диференційованого підходу до учнів // Початкова школа. - 1990. - № 6. – С.8- 11.
112. Скворцова С. Задачі на знаходження середнього арифметичного // Початкова школа. - 2002. - № 1. - С.23-28.
113. Страчар Е. Система і методи керівництва навчальним процесом. – К.: Радянська школа, 1982.
114. Сухомлинський В.О. Вибрані твори в 5 томах - Київ: Радянська школа, 1977. - Т.5. - 640 с.
115. Сучасний тлумачний словник української мови для школярів, абітурієнтів, студентів, викладачів / Уклад. Олексієнко Л.П., Шумейко О.Л. – Київ: Кобза, 2002. – 544 с.
116. Тадеєв В.О. Математика. Тлумачний словник-довідник. -Тернопіль.: Богдан, 1999. - 160 с.
117. Теоретичні основи педагогіки. Курс лекцій / За ред. О.Вишневського. – Дрогобич: Відродження, 2001. – 268 с.
118. Тягур Р.С. Внутрікласна диференціація // Початкова школа. - 1993. - № 11. - С.61-63.
119. Тягур Р.С. Ефективність системи диференційованого навчання // Початкова школа. - 1992. - № 11-12. - С.25-39.
120. Унт И. Индивидуализация и дефферениация обучения. - М.: Педагогіка, 1990. - 192 с.
121. Уткина Т.В. Дифференцированный подход к учащимся при выполнении ими домашнего задания по математике // Начальная школа. - 1984. - № 5.
122. Фельдштейн Д.И. Проблемы возрастной и педагогической психологии. - М.: Международная педагогическая академия, 1995. – 368 с.
123. Фіцула М.М. Педагогіка. – Київ: Академія, 2002. – 528 с.
124. Фоменкова М.В., Хаустова Н.Н. Дифференциация в обучении математике // Начальная школа. – 1999. - № 2. - С.50-52.
125. Фонин Д.С., Целищевап И.И. Моделирование как важное средство обучения решению задач // Начальная школа. – 1990. - № 3. - С.33-36.
126. Фридман К.Н., Волков К.Н. Психологическая наука учителю. - М.: Просвещение, 1988. – 224 с.
127. Фурман А.В. Психодіагностика в системі диференціації навчання. -К.: Освіта, 1993. - 224 с.
128. Хробот В. Різнорівневі завдання на уроках математики // Початкова школа. – 1997. - № 1. - С.20-25.
129. Чайка В. Основи дидактики. Тексти лекцій і завдання для самоконтролю. - Тернопіль.: Астон, 2002. - 244 с.
130. Чередов И.И. Формы учебной работы в средней школе. - М.: Просвещение, 1988. - 160 с.
131. Черних Л.В. Диференційований підхід у навчанні математики // Математика. - 2003. - №12. - С.4- 6.
132. Шевельова Л.О. Диференційоване навчання на уроках математики в початковій школі // Початкове навчання і виховання. - 2004. - № 29. - С. 2- 12.
133. Шевченко А. Про роботу над задачами із «зайвими» даними // Початкова школа. - 1999. - № 5. – С.28-30.
134. Эрдниев П.М., Эрдниев Б.М. Теория и методика обучения математике в начальной школе. – М.: Педагогіка, 1988. – 208 с.
135. Ягупов В.В. Педагогіка: Навчальний посібник. – К.: Либідь, 2003. – 560 с.
Додаток 1
Хід уроку
І. Організація класу до уроку.
Встали всі рівненько,
Усміхнулися гарненько.
Не дрімати, не лежати,
Лише думати й міркувати.
О.І. Дацко
Усні обчислення.
- Ведмедик хоче з вами пограти. Він увімкнув червоний, жовтий і зелений кольори світлофору.
(Дошка поділена на три частини (середній, достатній і високий рівні). На кожній з них макет гри. Учитель вивішує над кожною частиною дошки світлофор із певним кольором.)
- Хто який колір світлофора зможе увімкнути самостійно?
(Учні викладають на парті світлофор певного кольору – це дає змогу вчителю визначити, хто яке завдання вибрав.)
- Результати обчислень запишіть на планшетах. Час для виконання 3 хвилини.
Гра «Телефон».
(Світлофор зеленого кольору. Середній рівень.)
(За стрілками учні виконують обчислення, результати записують на планшетах.)
Гра «Математична квітка».
6+23 2+56
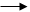
3+8 4-2
7-2
4+24
5+25
7+20
9-8 3+12
5-2
(Світлофор жовтого кольору. Достатній рівень.)
(За стрілками учні виконують обчислення, результати записують на планшетах.)
Гра «Ланцюжки».
(Світлофор червоного кольору. Високий рівень.)
(Учні виконують обчислення, результати записують на планшетах.)
Картка 1
Користуючись таблицями множення числа 6 і ділення на 6, розв’яжи приклади.
6 · 7 = ________ 6 · 5 +54 = _________
42 :6= ________ 6 · 4 – 11 = _________
Картка 2
Розв’яжи приклади.
6 · 8 + 14 = ___________ 6 · 9 – 23 = ___________
6 · 4 – 10 = ___________ 36 : 6 + 20 = __________
Розв’яжи приклади. Запиши їхню відповідь у порядку зростання.
(65-29) : 6 = ___________ 65 – 54 : 6 = ___________
36 + 42 : 6 = ___________ (39 +15) : : = ___________
Картка 3
Запиши вирази. Обчисли.
| Множник | 6 | 5 | 4 |
| Множник | (72 – 64) | (43 – 36) | (12 : 6) |
| Добуток |
· Перевірка виконання.
Підготовчі вправи.
- На планшетах намалюйте 2 трикутники. Під ними – 8 квадратів.
- На скільки більше квадратів, ніж трикутників? (На 6.)
- На скільки менше трикутників, ніж квадратів? (На 6.)
- Як ви дізналися? (8-2=6.)
- Який висновок можна зробити? (Щоб дізнатися на скільки одне число менше або більше, ніж друге, треба від більшого числа відняти менше.)
- А зараз завдання від зайчика.
На одну поличку поклали 3 книжки, а на другу – чотири рази по три книжки.
- Скільки виклали книг на другу полицю? (12 книг.)
- Що можна сказати про кількість книжок на першій полиці порівняно з кількістю на першій? (Їх у 4 рази більше.)
- Який можна зробити висновок? (Щоб дізнатися, у скільки разів одне число більше або менше, ніж друге, треба більше число поділити на менше.)
2. Первинне закріплення. Робота на планшетах.
Перший етап. Колективне завдання.
- Перше число 15, друге – 3. у скільки разів друге число менше, ніж перше? (У 5 разів.)
(Учні, які обчислили правильно, викладають на парті («вмикають») червоний колір світлофора і виконують самостійно завдання першого варіанту (див. таблицю). З рештою учнів учитель розв’язує № 221 і додаткове завдання на планшетах.)
· Робота над № 221.
- У скільки разів більше синіх фігур, ніж червоних?
- Як ви про це дізналися?
- Складіть вираз.
· Робота на планшетах.
- Перше число 21, друге – 3. у скільки разів друге число менше, ніж перше? (У 7 разів.)
(На цей раз, хто виконав правильно, викладає на парті світлофор жовтого кольору.)
· Перевірка виконання завдання.
Другий етап.
(Учні, які самостійно впоралися із завданнями першого етапу, відповідно розв’язують завдання першого і другого варіантів (див. таблицю). З рештою учнів учитель працює над завданням № 222. хто самостійно впорається із завданням, викладає світлофор зеленого кольору.)
Третій етап.
(Учні виконують завдання з таблиці по варіантах.)
| І варіант | ІІ варіант | ІІ варіант | |
| Перший етап | 1.У скільки разів 42 більше, ніж 6? 2.У скільки разів 6 менше, ніж 48? | ||
| Другий етап | В одному ряду 12 яблунь. У другому ряду 6 яблунь. У скільки разів більше яблунь в першому ряду, ніж у другому? | У скільки разів 24 більше, ніж 6? У скільки разів 6 менше, ніж 42? | |
| Третій етап | Складіть задачу про масу курки й індика. | В одному відрі 18 кг картоплі,а в другому – 6 кг картоплі. У скільки разів менше картоплі в другому відрі, ніж в першому? | У скільки разів 18 більше, ніж 6? У скільки разів 6 менше, ніж 54? |
Фізкультхвилинка.
Щось втомились ми сидіти.
Треба трохи відпочити.
Руки вгору, руки вниз,
На сусіда подивись.
Руки вгору, руки в боки,
І зроби чотири скоки.
Ось так. Ось так, ось так!
Плесніть у долоньки раз.
За роботу! Все гаразд!
V. Закріплення вивченого
Робота з підручником.
- Лисичка принесла нам підручник і пропонує продовжити роботу.
а) № 219.
- Як ви дізналися, що відрізок АВ у 5 разів коротший за відрізок КМ?
- Про що ще ви дізналися, виконавши цю дію?
б) № 223.
Учні обчислюють числові вирази з коментуванням.
в) Задача № 224.
Учні колективно аналізують умову задачі. Хто може, розв’язують самостійно, решта – під керівництвом учителя.
Другий етап.
(Учні, які розв’язують задачу самостійно (червоний колір світлофора), потім отримують завдання скласти вираз до задачі. З рештою учнів учитель складає план розв’язування задачі.)
- Чи можемо відразу дізнатися, скільки років синові? Чому? (Ні. Тому що не знаємо, скільки років мамі.)
- Чи можемо дізнатися, скільки років мамі? Що означає «на 4 роки молодша»? (Їй на 4 роки менше, ніж татові.)
- Хто може самостійно розв’язати задачу, «увімкніть» жовтий колір світлофора.
Третій етап.
(Учні, які «увімкнули» червоні і сині кольори світлофора виконують додаткові завдання (за вибором учителя). Решта викладають на парту зелений колір світлофора і записують розв’язання задачі під керівництвом учителя.)
VI. Домашнє завдання
Виконати №№ 226, 227. До № 227 додаткове завдання: «Скільки літрів пального потрібно для 4 годин роботи такого двигуна?» (для учнів, у яких найбільше червоного кольору світлофора).
VII. Підсумок уроку
- У кого якого кольору світлофори «світили» впродовж уроку?
- Чиї завдання були для вас найцікавішими? (Учні називають імена казкових героїв.) А чиє було важким для виконання? (Учні називають імена казкових героїв.)
Заходить сонечко за гай,
Казкові герої кажуть: «Бувай!»
- І ми скажемо їм: «Бувайте! До наступної зустрічі на уроці».
Додаток 2
Завдання 1
Усно склади задачу за даними таблиці. Запиши запитання задачі, її розв’язання і відповідь.
| Щоденна витрата | Кількість днів | Усього витратили |
| Однакова | 7 5 | 42 кг ? |
Картка 1
1. Розглянь короткий запис задачі у таблиці.
2. З’ясуй, чи відповідає цьому запису такий зміст.
За однакової щоденної норми кінь з’їдає за 7 днів 42 кг сіна. Скільки кілограмів сіна потрібно коневі за 5 днів?
3. Розв’яжи задачу, користуючись схемою.
1) 1 : 1 = 1 (кг)
2) 1 · 1 = 1 (кг)
4. Поясни, про що дізналися в кожній дії.
5. Запиши відповідь.
Картка 2
1. Розглянь короткий запис задачі.
2. З’ясуй, чи відповідає цьому запису така умова.
За однакової щоденної норми кінь з’їдає за 7 днів 42 кг сіна.
3. Постав запитання до задачі і розв’яжи її окремими діями з поясненням.
4. Запиши відповідь.
Картка 3
1. Розв’яжи задачу за даними таблиці.
2. Запиши розв’язання, склавши числовий вираз.
3. Запиши відповідь.
Додаткове завдання
Як зміниться відповідь за умови, що за 7 днів витратили 56 кг?
Завдання 2
З одного куща смородини зібрали 18 кг ягід, а з другого – 12 кг. Усі ягоди розклали в ящики, по 6 кг у кожний. Скільки ящиків потрібно для цього? (Розв’яжи задачу двома способами.)
Картка 1
1. Прочитай задачу.
2. Розглянь скорочений запис задачі у таблиці.
| Маса 1 ящика смородини |  Кількість ящиків
| Загальна маса |
| Однакова по 6 кг | 1 ? 1 | 18 кг 12 кг |
3. Розв’яжи задачу двома способами за схемами.
І спосіб
1) 1 : 1 = 1 (ящ.)
2) 1 : 1 = 1 (ящ.)
3) 1 + 1 = 1 (ящ.)
ІІ спосіб
1) 1 + 1 = 1 (кг)
2) 1 : 1 = 1 (ящ.)
4. Запиши відповідь.
Картка 2
1. Прочитай задачу і знайди опорні слова для її розв’язання.
2. Розв’яжи задачу спочатку двома діями, а потім – трьома діями.
3. Запиши відповідь.
Картка 3
1. Прочитай задачу і розв’яжи її двома способами, склавши числові вирази.
2. Запиши відповідь.
Додаткове завдання
Як зміниться відповідь, якщо маса одного ящика смородини становитиме 3 кг?
Завдання 3
Картка 1
1. Прочитай задачу.
2. Повтори задачу за коротким записом.
І - 127 кг
450 кг ІІ – на 65 кг більше
ІІІ - ?
3. Розв’яжи задачу трьома діями з поясненням.
4. Перевір відповідь (131 кг).
Картка 2
1. Прочитай задачу і підкресли опорні слова.
2. Склади усно план розв’язування задачі окремими діями.
3. Запиши розв’язування задачі окремими діями.
4. Запиши відповідь і зроби перевірку.
Перевірка. 1 + 1 + 1 = 450 (кг)
Картка 3
1. Прочитай і розв’яжи задачу, склавши вираз.
Додаткове завдання
Завдання 4
Картка 1
1. Прочитай задачу і розглянь скорочений запис.
І – 126 учнів
1/3 становили учні четвертих класів
ІІ – у 3 рази більше
Скільки четвертокласників відвідало виставку?
2. Розв’яжи задачу за планом.
1) Скільки учнів відвідало виставку другого дня?
2) Скільки учнів відвідало виставку за два дні?
3) Скільки четвертокласників відвідало виставку?
3. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розглянь схему розв’язання задачі.
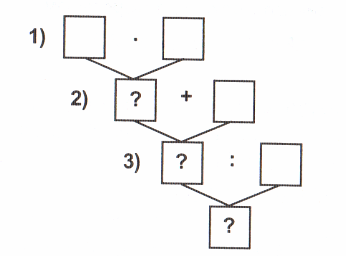
3. Запиши окремо кожну дію і пояснення до неї.
4. Склади обернену задачу за скороченим записом.
І – 154 учні
1/7 становили учні третіх класів
ІІ - у 2 рази менше
Скільки третьокласників відвідало виставку?
5.Розв’яжи задачу, склавши вираз.
2. Запиши відповідь.
Картка 3
1. Прочитай задачу.
2. Запиши розв’язання задачі з поясненням.
3. Зміни запитання так, щоб задача розв’язувалася 4 діями.
4. Як зміниться відповідь до задачі, якщо слово «більше» змінити словом «менше»?
Завдання 5
Картка 1
1. Прочитай задачу.
2. Повтори задачу, виділивши опорні слова для розв’язування.
3. Заповни «віконечка» і встав відповідну дію замість зірочок.
1 кг – змололи всього пшениці;
1 * 1 (кг) – становили висівки;
828 - 1 * 1 (кг) - одержали борошна;
(828 - 1 * 1) : 1 - вийшло пакетів з борошном.
4. Розв’яжи задачу, обчисливши значення останнього виразу.
5. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу, обчисливши значення останнього виразу.
3. Заповни «віконечка» числовими даними задачі і перевір правильність розв’язання.
1 · 1 + 138 = 828 (кг)
Картка 3
1. Прочитай задачу.
2. Усно склади план її розв’язування.
3. Розв’яжи задачу, склавши числовий вираз.
4. Запиши відповідь.
Додаткове завдання
Склади і розв’яжи подібну задачу за виразом:
828 – 2 · 345
Завдання 6
Картка 1
1. Прочитай задачу.
2. Повтори її за скороченим записом.
П. – 48 грибів
М. – у 12 разів менше ? грибів
Н. – на 8 грибів менше
3. Розв’яжи задачу за планом.
1) Скільки грибів зібрав Мишко?
2) Скільки грибів зібрала Наталка?
3) Скільки грибів зібрали діти?
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу окремими діями з поясненням.
Картка 3
1. Розв’яжи задачу, склавши вираз.
2. Запиши відповідь.
Додаткове завдання
 |
1. Зміни запитання задачі, щоб вона розв’язувалася за схемою.
2. Запиши розв’язання і відповідь.
Завдання 7
Картка 1
1. Прочитай задачу.
2. Розглянь ілюстрацію до задачі.
Сира кава 1 1 1 111 111 111
Смажена кава 2 кг 2 кг 2 кг 2 кг
3. Розв’яжи задачу за планом.
1) Скільки разів по 3 кг вміститься у 12 кг?
2) Скільки кілограмів смаженої кави вийде з 13 кг сирої ?
4. Запиши відповідь.
Картка 2
1. Прочитай задачу і запиши її скорочено.
2. Склади і запиши план розв’язування.
3. Розв’яжи задачу за планом.
4. Запиши відповідь.
Картка 3
1. Розв’яжи задачу, склавши числовий вираз.
2. Запиши відповідь.
Додаткове завдання
1. Дізнайся, скільки кілограмів смаженої кави вийде 3 18 кг (30кг, 150 кг) сирої.
2. Запиши обчислення і відповідь.
Завдання 8
Картка 1
1. Прочитай задачу.
2. Розглянь ілюстрацію.
 |
3.Розв’яжи задачу за планом і запиши розв’язання окремими діями.
1) Скільки літрів води залишилось в цистернах, коли з однієї взяли 1000 кг?
2) Скільки літрів води було в другій цистерні?
3) Скільки літрів води було в першій цистерні?
4. Запиши відповідь.
Картка 2
1. Розв’яжи задачу.
2. Запиши відповідь.
 |
Додаткове завдання
1. У задачі зміни число 5000 л числом 3000 л.
2. Розв’яжи задачу і запиши відповідь.
Картка 3
1. Розв’яжи задачу, склавши числовий вираз за схемою.
Додаткове завдання
1. У задачі заміни число 1000 л числом 800 л.
2. Розв’яжи задачу письмово і запиши відповідь.
Завдання 9
Десятиметрову колоду розрізали на 8 рівних частин, а семиметрову – на 5. Шматки (відрізки) якої колоди довші?
Картка 1
1. Прочитай задачу.
2. Зверни увагу на слова: десятиметрова і семиметрова колоди, тобто колоди, що мають довжину 1 м і 1 м.
Вказівка! Перетвори довжину колод у менші міри (сантиметри).
1) 1 м = 1 см; 2) 1 м = 1 см.
3. Встав пропущені числа і розв’яжи задачу.
1) 1 : 8 = 1 (см) – довжина відрізка десятиметрової колоди;
2) 1 : 5 = 1 (см) – довжина відрізка семиметрової колоди;
3) 1 - 1 = 1 (см) – довший відрізок ______________ колоди.
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Перед розв’язанням перетвори більші одиниці довжини в менші.
3. Розв’яжи задачу, записуючи план розв’язання.
4. Запиши відповідь.
Картка 3
1. Прочитай і розв’яжи задачу.
2. Запиши відповідь.
Додаткове завдання
1. Зміни запитання задачі так, щоб остання дія була додавання.
2. Розв’яжи задачу, склавши вираз.
3. Запиши відповідь.
Завдання 10
За 3 місяці завод випустив 4603 автомобілі. Скільки автомобілів випустив завод окремо за кожний місяць, якщо за перший і другий місяці він випустив 2978 автомобілів, а за перший і третій місяці – 3093 ?
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
 |
3. Розв’яжи задачу за планом.
1) Скільки автомобілів випустив завод за другий місяць?
2) Скільки автомобілів випустив завод за третій місяць?
3) Скільки автомобілів випустив завод за перший місяць?
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Закінчи скорочений запис задачі.
ІІ –
… авт. І – … авт.
ІІІ - … авт.
3. Розв’яжи задачу окремими діями з поясненням.
4. Зроби перевірку.
Картка 3
1. Прочитай задачу.
2. Розв’яжи її, записуючи план розв’язування.
1) Скільки автомобілів випустив завод за третій місяць?
2) ______________________________________________
3) _______________________________________________
3. Запиши відповідь.
4. Зроби перевірку.
Завдання 11
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
І – 4 см 8 мм
12 см 6 мм ІІ – 3 см 9 мм
ІІІ - ?
Вказівка! Перетвори більші одиниці вимірювання довжини в менші.
3. Розв’яжи задачу окремими діями з поясненням.
4. Запиши відповідь.
5. Зроби перевірку за схемою.
1 + 1 + 1 = 12 см 6 мм
Картка 2
1. Прочитай задачу.
Вказівка! Перетвори більші одиниці вимірювання довжини в менші.
2. Розв’яжи задачу, записуючи план розв’язування.
3. Запиши відповідь.
4. Зроби перевірку.
Картка 3
1. Прочитай задачу.
Вказівка! Перетвори більші одиниці вимірювання довжини в менші.
2. Розв’яжи задачу, склавши числовий вираз.
3. Запиши відповідь.
4. Зроби перевірку
Додаткове завдання
Склади і розв'яжи обернену задачу.
 І - 1
? ІІ - 1
ІІІ - 1
|
Завдання 12
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
І – 13 750 м
? ІІ – стільки, скільки першого дня
ІІІ – на 11 800 м менше
3.
4. Закінчи розв’язування задачі.
1) 1 + 1 = 1 (м) – виробила фабрика за два дні;
2) 1 - 1 = 1 (м) – виробила фабрика третього дня;
3) 1 + 1 = 1 (м) – виробила фабрика за три дні.
5. Запиши відповідь.
Картка 2
1. Прочитай задачу. Зверни увагу на другий день роботи фабрики.
2. Розв’яжи задачу, записуючи план розв’язування.
3. Запиши відповідь.
Додаткове завдання
1. Дізнайся. На скільки більше метрів тканини виробила фабрика третього дня, ніж другого.
2. Запиши обчислення і відповідь
Картка 3
1. Прочитай задачу.
2. Розв’яжи задачу окремими діями з поясненням.
3. Запиши відповідь.
Додаткове завдання
1. Склади і розв’яжи обернену задачу, в якій шуканим числом буде кількість тканини, виробленої першого дня.
2. Запиши обчислення і відповідь.
Завдання 13
Картка 1
1. Прочитай задачу.
2. Повтори задачу за коротким записом.
| Швидкість | Час | Відстань | |
| Йшли Їхали | 4 км/ год 45 км/ год | 2 год 3 год |  ?
|
3. Розв’яжи задачу трьома діями з поясненням.
4. Запиши відповідь.
Картка 2
1.Прочитай задачу.
2. Розв’яжи задачу, склавши числовий вираз.
3. Запиши відповідь.
Додаткове завдання
1. Дізнайся, на скільки кілометрів більше туристи проїхали автобусом, ніж пройшли.
2. Запиши обчислення і відповідь.
Картка 3
1. Прочитай задачу і розв’яжи її.
2. Заміни числа 4 км/ год на 6 км/ год, 45 км/ год на 60 км/ год.
3. Розв’яжи нову задачу, склавши числовий вираз.
4. Запиши відповідь.
Додаткове завдання
1. Склади обернену задачу, в якій шуканим буде число 60 км / год.
| Швидкість | Час | Відстань | |
| Йшли Їхали | 1 ? | 1 1 | 1 1 |
2. Запиши відповідь.
Завдання 14
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
| Обсяг води, викачаної за 1 хв | Час роботи | Всього води |
| 1 л 1 л | 24 хв 40 хв | 4800 л |
| За скільки хвилин викачають всю воду обидва насоси, працюючи разом? | ||
3. Закінчи розв’язання задачі.
1) _____________________ - викачував за 1 хв перший насос;
2) _____________________ - викачував за 1 хв другий насос;
3) _____________________ - можуть викачати за 1 хв два насоси, разом;
4) _____________________ - час, протягом якого два насоси можуть вика-
чати всю воду.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу, записуючи план розв’язування.
3. Запиши відповідь.
Картка 3
1. Прочитай задачу.
2. Склади числовий вираз розв’язування задачі та обчисли його значення.
3. Запиши відповідь.
Додаткове завдання
1. Дізнайся, за скільки хвилин викачають воду два насоси меншої потужності.
2. Запиши обчислення і відповідь.
Завдання 15
Картка 1
1. Прочитай задачу.
2. Розглянь малюнок до задачі.
 |
З якою швидкістю летів супутник?
3. Розв’яжи задачу, заповнивши пропуски.
1) 1 : 1 = 1 (км) – пролетів супутник за 10 с;
2) 1 : 1 = 1 (км/с) – швидкість супутника
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи її, записуючи план розв’язування.
3. Запиши відповідь.
Додаткове завдання
1. Дізнайся, за скільки секунд супутник пролетить відстань 320 км.
2. Запиши обчислення і відповідь.
Картка 3
1. Прочитай і розв’яжи задачу двома способами, склавши числові вирази.
2. Запиши відповідь.
Додаткове завдання
Склади усно обернену задачу, в якій відстань довжиною 320 км є шуканим числом.
Завдання 16
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
| Швидкість | Час | Відстань | |
| Туди Назад | 12 км/год ? | 5 год 6 год | Однакова |
Пригадай! Як знайти відстань? Як знайти швидкість?
3. Розв’яжи задачу окремими діями з поясненням.
4. Запиши відповідь.
Додаткове завдання
1. Чому на зворотний шлях велосипедист затратив більше часу?
2. Яку загальну відстань проїхав велосипедист?
Картка 2
1. Прочитай задачу.
2. Розв’яжи її, записуючи план розв’язування.
3. Запиши відповідь.
Додаткове завдання
1. Заміни запитання задачі так, щоб вона розв’язувалася трьома діями.
2. Запитання й обчислення запиши.
Картка 3
1. Прочитай задачу.
2. Розв’яжи її, склавши числовий вираз.
3. Запиши відповідь.
Додаткове завдання
Дізнайся, за скільки годин велосипедист зміг би проїхати всю відстань, якби він рухався зі швидкістю 15 км/год.
Завдання 17
Один оператор набирає за день на комп’ютері 20 сторінок тексту, а другий - 24 сторінки. Скільки сторінок вони наберуть за k днів, якщо будуть працювати разом? Склади вираз для розв’язування задачі та обчисли його значення, якщо k= 5.
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
| Набирає за день | Кількість днів | Всього сторінок | |
| Перший оператор Другий оператор | 20 ст. 24 ст. | k k |  ?
|
3. Розв’яжи задачу поступовим складанням виразу.
20 · k (ст.) – всього набрав перший оператор;
1 · 1 (ст.) - ______________________________;
1 · 1 + 1 · 1 - ___________________________.
4. Обчисли значення виразу, якщо k = 5.
5. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи її двома способами окремими діями з поясненням.
3. Запиши відповідь.
Картка 3
1. Розв’яжи задачу зручним способом.
2. Запиши відповідь.
Додаткове завдання
Склади і розв’яжи обернену задачу, в якій треба дізнатися, скільки сторінок за день набирає перший оператор.
| Набирає за день | Кількість днів | Всього сторінок | |
| Перший оператор Другий оператор |
Завдання 18
План розв’язування
1) Скільки тонн води викачає перший насос за 1 год7
2) Скільки тонн води викачує другий насос за 1 год?
3) Скільки тонн води викачають обидва насоси за 1 год?
4) За скільки годин буде викачано 24 т води?
Картка 1
1. Прочитай задачу і розглянь ілюстрацію.
| Продуктивність | Час | Разом | |
| Перший насос Другий насос Разом | 1 O 1 + O | 6 год 3 год ? | 24 т |
2. Розглянь план розв’язування задачі.
3. Подумай, яку дію треба виконати до кожного запитання.
4. Запиши план і відповідні дії. Обчисли їх значення.
5. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу за планом окремими діями з поясненням.
3. Запиши відповідь
Картка 3
1. Прочитай і розв’яжи здачу за поданим планом, склавши вираз.
2. Запиши відповідь.
Додаткове завдання
1. Зміни запитання задачі відповідно до виразу.
(24 : 6 + 24 : 3) · 4
2. Знайди значення виразу і запиши відповідь.
Завдання 19
Картка1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
Капусти - 248 ц
   Буряків – у 2 рази менше ?
Моркви – на 84 ц менше
|
3. Розв’яжи задачу, записуючи план розв’язування.
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу окремими діями з поясненням.
3. Запиши відповідь.
Додаткове завдання
1. Скільки потрібно пакетів, щоб розкласти буряки і моркву по 2 кг?
2. Обчислення і відповідь запиши.
Картка 3
1. Прочитай і розв’яжи задачу, склавши числовий вираз.
2. Запиши відповідь.
Додаткове завдання
1. Припустимо, що четверту частину всіх овочів віддали в шкільну їдальню, а решту залишили для годівлі кролів. Скільки центнерів овочів залишили для кролів?
2. Обчислення і відповідь запиши.
Завдання 20
Від двох протилежних берегів озера одночасно попливли назустріч один одному два човни. Перший човен плив зі швидкістю 7 км/год, а другий – 8 км/год. Човни зустрілися через 3 год. Знайдіть відстань між берегами озера.
Картка 1
1. Прочитай задачу.
 |
2. Розглянь малюнок до задачі.
3. Розв’яжи задачу за поданим планом.
1) На скільки кілометрів зближаться човни за 1 год?
2) Яка відстань між берегами озера?
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу двома способами окремими діями з поясненням.
3. Запиши відповідь.
Картка 3
1. Прочитай задачу.
2. Розв’яжи її, склавши числовий вираз.
3. Запиши відповідь.
Додаткове завдання
1. Склади обернену задачу за малюнком.
 |
2. Розв’яжи обернену задачу і запиши відповідь.
Завдання 21
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
| Перевозить за 1 рейс | Кількість рейсів | Всього перевозить | |
| Автомобіль ГАЗ Автомобіль більшої вантажн. | 1 1 | 24 12 | 600 ц 600 ц |
| За скільки рейсів можуть перевезти вугілля обидва автомобілі | |||
3. Впиши відповідні числа і розв’яжи задачу.
1) 1 : 1 = 1 (ц) – перевозить за один рейс автомобіль;
2) 1 : 1 = 1 (ц) – перевозить за один рейс інший автомобіль;
3) 1 + 1 = 1 (ц) – можуть перевезти за один рейс обидва автомобілі;
4) 1 : 1 = 1 (р.) - за скільки рейсів перевезуть все вугілля обидва автомобілі.
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу, записуючи план розв’язування.
3. запиши відповідь.
Картка 3
1. Прочитай задачу.
2. Склади числовий вираз для розв’язування задачі і знайди його значення.
3. Запиши відповідь.
Завдання 22
Картка 1
1. Прочитай задачу.
2. Повтори зміст задачі за скороченим записом.
| Виростив – 1445 ц Продав - ? 5/6 решти Залишив – 245 ц |
3. Розв’яжи задачу. Вставляючи пропущені числа.
1) 1 - 1 = 1 (ц) – решта картоплі;
2) 1 : 1 · 1 = 1 (ц) – продав фермер на базарі.
4. Запиши відповідь і зроби перевірку.
Картка 2
1. Прочитай задачу.
2. Розглянь графічний малюнок і розв’яжи задачу.
 |
3. Заміни зміст запитання задачі відповідно до малюнка.
4. Розв’жи складену задачу і запиши відповідь.
Картка 3
1. Прочитай задачу.
2. Склади числовий вираз розв’язання задачі і знайди його значення.
3. Запиши відповідь.
Додаткове завдання
Зроби перевірку розв’язання за умови, що 1/6 решти картоплі залишили для насіння.
Завдання 23
Лижник пройшов 560 км і йшов весь час з однаковою швидкістю. До зупинки він ішов 4 год, а після зупинки 3 год. Скільки кілометрів пройшов лижник після зупинки?
Картка 1
1. Прочитай задачу.
2. Розглянь її скорочений запис.
| Швидкість | Час | Відстань | |
| До зупинки Після зупинки | Однакова | 4 год 3 год | 1 56 км
?
|
3. Закінчи розв’язання задачі відповідно до записів.
1) _________________ - стільки годин був у дорозі лижник;
2) _________________ - швидкість, з якою рухався лижник;
3) _________________ - пройшов лижник після зупинки.
4. Запиши відповідь.
Картка 2
1. Прочитай задачу.
2. Розв’яжи задачу, склавши числовий вираз.
3. Запиши відповідь.
Додаткове завдання
1. Склади і розв’яжи обернену задачу, в якій шуканим буде число 56 км.
2. Запиши обчислення і відповідь.
Картка 3
1. Прочитай задачу.
2. Запиши відповідь.
Додаткове завдання
1. Склади і роз’яжи обернену задачу, в якій шуканим буде час руху лижника до зупинки.
2. Склади таблицю зі скороченим записом задачі.
Завдання 24
 |
Першого дня господарство відправило на сезонний ярмарок 4 машини з капустою, а другого – 7 таких машин. Другого дня відправлено на 9 т капусти більше, ніж першого. Скільки тонн капусти відправлено другого дня?
Картка 1
1. Прочитай задачу і розглянь малюнок.
2. Розглянь графічний малюнок.
І дн.
 |
ІІ дн.
3. Розв’яжи задачу за планом.
1) На скільки більше машин відправлено другого дня, ніж першого?
2) Яка вантажність однієї машини?
3) Скільки тонн капусти відправлено другого дня?
4. Запиши відповідь.
Додаткове завдання
1. Дізнайся, скільки тонн капусти відправлено першого дня?
2. Запиши обчислення і відповідь.
Картка 2
1. Прочитай задачу і розглянь таблицю з коротким записом.
| Вантажність 1 машини | Кількість машин | Загальна маса | |
| І дня ІІ дня | Однакова | 4 7 |   1
на 9 т більше
|
2. Розв’яжи задачу окремими діями з поясненням.
3. Запиши відповідь.
Додаткове завдання
1. Дізнайся, скільки тонн капусти відправлено за два дні.
2. Обчислення і відповідь запиши.
Картка 3
1. Прочитай задачу і розглянь малюнок в підручнику.
2. Склади числовий вираз і розв’яжи задачу.
3. Запиши відповідь.
Додаткове завдання
1. Зміни і запиши запитання задачі так, щоб вона розв’язувалася виразом.
9 : (7 – 4) · (7 + 4)
2. Обчислення значення виразу і запиши відповідь.
Диференційований підхід у процесі навчання молодших школярів розв’язувати текстові задачі
Зміст
Вступ
Розділ І. Психолого-педагогічні основи диференційованого підходу в процесі вивчення математики учнями початкових класів
1.1 Враховування навчальних можливостей учнів як основа диференційованого підходу у навчанні
1.2 Характеристика основних видів диференційованого навчання
Розділ ІІ. Методика використання диференційованого підходу при навчанні учнів розв’язуванню текстових задач
2.1 Пошук шляхів вдосконалення методики формування вмінь молодших школярів розв’язувати текстові задачі
2.2 Організація і зміст експериментального дослідження
2.3 Аналіз ефективності експериментального дослідження
Висновки
Список використаної літератури
Додатки
Вступ
Проектом Державного стандарту загальної середньої освіти передбачається диференційоване навчання учнів початкових класів, а за мету курсу математики ставиться досягнення кожним учнем рівня навченості не нижче обов’язкового. Нові вимоги вимагають нових технологій навчання, які б забезпечили і високий рівень теоретичної та практичної підготовки з математики, і переорієнтацію навчально-виховного процесу на особистість учня, на сприятливі умови для досягнення кожним належного рівня знань, умінь і навичок.
Дані, необхідні для осмислення цілісності і цілеспрямованості формування вмінь розв’язувати текстові задачі в умовах диференційованого навчання, одержані нами в результаті аналізу психологічної і методичної літератури, де є немало цінних ідей і теоретичних узагальнень. Так, праці в галузі педагогічної психології (Л.С. Виготський, П.Я. Гальперін, Г.С. Костюк, О.М. Леонтьєв, Н.Ф. Тализіна, І.С. Якиманська) розкривають зміст поняття ”вміння” і розуміння механізмів його формування у школярів початкової школи. Психологічний та методичний аспект процесу розв’язування задач досліджували Г.О. Балл, Л.Л. Гурова, С.Д. Максименко, Є.І. Машбиць, Н.О. Менчинська, Н.А. Побірченко, З.І. Слєпкань, Л.М. Фрідман. Психолого-педагогічні і методичні основи диференційованого навчання розкрито в працях М.І. Бурди, Ю.З. Гільбуха, О.С. Дубинчук, С.О. Логачевської, О.Я. Савченко, І.Е. Унт та ін.
До проблеми розв’язування задач при вивченні математики тією чи іншою мірою зверталися відомі методисти. Особливу увагу розв’язуванню задач як засобу розвитку мислення, формування системи математичних понять, добору задач до підручників у середній школі приділяли Г.П. Бевз, Ю.М. Колягін, І.Ф. Тесленко, А.А. Столяр, Л.М. Фрідман, у початковій школі - М.О. Бантова, Г.В. Бельтюкова, М.В. Богданович, Г.В. Гап’юк, М.М. Левшин, М.Г. Моро, Я.А. Король, Л.П. Кочіна, А.С. Пчолко, Н. Уткіна та інші.
Як відомо, навчально-виховний процес повинен будуватися відповідно до потреб особистості та індивідуальних можливостей дітей, зростання їх самостійності й творчої активності. А це вимагає організації навчання відповідно до здібностей, здатності до навчання, таланту дитини [85,6].
Використання індивідуального підходу та диференційованих форм навчальної роботи зумовлюється і впливом гуманістичної тенденції у вихованні школярів. Як правило, «обраний учителем середній темп діяльності є нормальним лише для певної частини учнів, для інших він швидкий чи повільний. Одна і та ж учбова задача для одних дітей є складною, майже нерозв’язною проблемою, а для інших вона – легке питання. Один і той самий текст одні діти розуміють після першого читання, іншим необхідне повторення, а третім – пояснення» [63, 51].
Таким чином, успішність засвоєння навчального матеріалу, темп оволодіння ним, міцність збереження та рівень осмисленості знань залежать не лише від діяльності педагога, але й від пізнавальних можливостей і здібностей учнів, обумовлених багатьма чинниками: особливостями сприймання, пам’яті, мислительної діяльності, а також фізичним розвитком і т. ін. Тому «кожен учитель має створити такі умови, за яких стало б можливим використання фактичних і потенційних можливостей кожної дитини за класно-урочної форми навчання» [42, 11]. Розв’язання цього практичного завдання тісно пов’язане з послідовною реалізацією диференційованого та індивідуального підходу до школярів.
Рівень навчально-пізнавальної активності молодших школярів може істотно підвищитися за умови диференційованого підходу до організації навчально-виховного процесу [49,20].
Програму навчання математики в початковій школі побудовано так, щоб реалізувати багаті потенційні можливості дитини: перетворити її природну допитливість на стійкий пізнавальний інтерес, а жвавість, активність спрямувати в річище дослідницької діяльності [41,21].
Зміст диференційованого навчання вчитель визначає відповідно до змісту і конкретних завдань кожного уроку. З метою організації практичної діяльності учнів слід широко застосовувати індивідуальний роздатковий матеріал, диференційовані завдання на уроках математики [62,9].
Важливим аспектом методу диференційованого підходу вважається те, що учні самостійно вибирають зміст і обсяг роботи для себе. І ніхто не диктує, як працювати сьогодні. На кінець уроку у дитини є задоволення від зробленої роботи. У слабших учнів не виникає комплексу нижчевартості, вони починають вірити у власні сили.
Традиційна методика формування вмінь розв’язувати задачі орієнтована на «середнього» учня. Вона не враховує зміст та основні ідеї проекту Державного стандарту загальної середньої освіти в Україні, зокрема ідеї рівневої диференціації навчання й орієнтацію її результатів на можливості школярів в процесі навчання. Не всі підручники з математики для початкових класів спрямовані на диференційоване формування вмінь розв’язувати задачі. Окремі з них не мають навчального матеріалу для організації ефективної роботи різних за здібностями груп учнів.
Отже, вивчення психологічної, педагогіко-методичної літератури, аналіз досвіду вчителів-практикантів з проблеми диференційованого підходу до учнів у процесі навчання молодших школярів розв’язувати задачі підтверджують актуальність обраної теми дослідження, особливо в умовах переходу на нові програми і підручники. Виявлення шляхів удосконалення методики формування вмінь розв’язувати текстові задачі в умовах диференційованого навчання у початкових класах складає проблему нашого дослідження.
Об’єкт дослідження – процес навчання математики молодших школярів.
Предмет дослідження – формування вмінь учнів початкових класів розв’язувати текстові задачі в умовах диференційованого навчання.
Метою дипломної роботи є: розробити, теоретично обґрунтувати і експериментально перевірити добірку завдань для навчання розв’язувати текстові задачі в процесі диференційованої роботи.
Гіпотеза дослідження: якщо, навчаючи розв’язуванню текстових задач, враховувати зміст і операційний склад умінь, рівні програмових вимог їх формування, психолого-педагогічні засади вироблення вмінь, принципи добору знань, диференційованих за складністю, то це підвищить ефективність навчання учнів розв’язувати текстові задачі, а отже, рівень математичного розвитку школярів і підготовку їх в цілому.
Для реалізації мети дослідження необхідно роз’язати наступні завдання:
1) На основі аналізу психологічно-педагогічної і навчально-методичної літератури, практики навчання з’ясувати стан досліджуваної проблеми.
2) Узагальнити шляхи вдосконалення методики формування вмінь молодших школярів розв’язувати текстові задачі.
3) Розробити добірку завдань, диференційованих за складністю і спрямованих на вироблення вмінь розв’язувати текстові задачі в початковій школі.
4) Теоретично обґрунтувати та експериментально перевірити розроблену добірку диференційованих завдань для навчання учнів розв’язувати текстові задачі.
Під час написання дипломної роботи були використані такі методи педагогічного дослідження: аналіз наукової літератури; спостереження; бесіди; експеримент; узагальнення експериментальних даних.
Практичне значення дипломної роботи зумовлюється актуальними завданнями удосконалення навчально-виховного процесу та його важливого компонента – уроків математики. Окрім того, теоретично окреслено та практично втілено диференційований підхід при навчанні учнів розв’язуванню задач. Тому матеріали дослідження можуть бути використані учителями початкової школи та студентами факультету підготовки вчителів початкових класів.
Дипломна робота складається із вступу, двох розділів, списку використаної літератури.
Дата: 2019-05-29, просмотров: 216.
