Исходные значения величин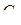 
и 
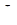представлены в таблице 5:
Таблица 5
|
|
|
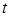
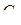
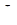
| 1 | 220063 | 85000 |
| 2 | 231828 | 78115 |
| 3 | 207359 | 71230 |
| 4 | 218337 | 64345 |
| 5 | 207851 | 57460 |
| 6 | 202994 | 50575 |
| 7 | 195524 | 43690 |
| 8 | 203944 | 36805 |
| 9 | 201672 | 29920 |
| 10 | 186648 | 23035 |
| 11 | 187864 | 16150 |
| 12 | 185659 | 9265 |
| 13 | 193932 | 2380 |
| 14 | 187232 | 85 |
Эндогенные переменные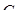 
, 
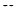выражаем через экзогенную переменную 
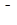. С этой целью подставляем выражение (4.6) в (4.7):
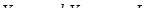(4.8)
отсюда получаем:
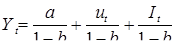(4.9)
Подставляем выражение (4.9) в уравнение (4.6) и получаем:
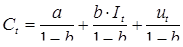(4.10)
Данное уравнение не содержит в правой части эндогенных переменных, а имеет только экзогенную переменную в виде 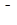(инвестиций). Экзогенная переменная не коррелирует со случайной составляющей 
и, следовательно, параметры этого уравнения могут быть найдены с помощью МНК.
Представим это уравнение в следующем виде:
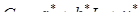(4.11)
где
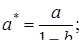
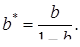
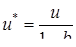(4.12)
Используя имеющиеся в таблице 5 данные о величинах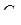 
и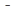 
, находим с помощью МНК несмещенные оценк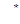и 
и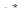 
из уравнения:
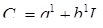(4.13)
где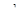 
- несмещенная оценка , 
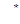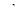- несмещенная оценка .
|
|
|
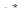| 184280,63 | 0,44 |
После определения значений a1 и b1 необходимо определить несмещенные оценки величин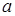 
и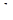 
, использовав соотношения:
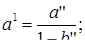
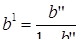(4.14)
где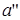 
, 
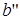- соответственно несмещенные оценки , .
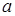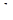Сами значения величин 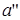, 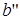определяем по формулам:
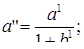
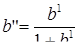(4.15)
|
|
|
| 127811,09 | 0,31 |
Использовав найденные значения 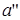и 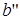, записываем уравнение функции потребления (4.6):
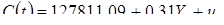
Сравниваем найденные по формуле (4.15) значения 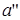и 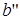с величинам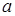и и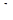 
, заданными в таблице 1 ( 
, 
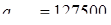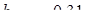) и рассчитываем проценты несовпадения данных величин по формулам:
; 
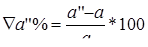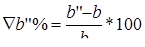(4.16)
; 
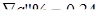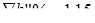
ЗАКЛЮЧЕНИЕ
Рассматривая классическую модель Кейнса можно сказать, что она не может достаточно хорошо описывать современную экономику и является устаревшей. Сейчас экономисты используют неокейнсеанскую модель, которая является более совершенной по сравнению с классической.
В представленной квалификационной работе были рассмотрены различные виды равновесных моделей, с учётом влияния входящих параметров и иных факторов.
Был приведён алгоритм вычисления показателей и экономический анализ полученных результатов.
В работе приводятся примеры демонстрирующие: экономическую ситуацию относительно фиксированной цены труда; кейнсианскую модель общего экономического равновесия.
СПИСОК ЛИТЕРАТУРЫ
1. Сидорович А. В. Курс экономической теории / А. В. Сидорович – М.: Дело и Сервис, 2001. – 832 с.
2. Лебедев В. В. Математическое моделирование социально-экономических процессов / В. В. Лебедев – М.: Изограф, 1997. – 224 с.
3. Борисовская Т. А. Экономическая теория / Т. А. Борисовская – М.: ИМПЭ им. А. С. Грибоедова, 2006. – 384 с.
4. Матвеева Т. Ю. Введение в макроэкономику / Т. Ю. Матвеева – М.: Изд. дом ГУ ВШЭ, 2007. – 512с.
5. Тарасевич Л. С. Учебник по Макроэкономике / Л. С. Тарасевич, П. И. Гребенников, А. И. Леусский – М.: Высшее образование, 2006. – 654 с.
6. Шагас Н. Л. Макроэкономика – 2 / Н. Л. Шагас, Е. А. Туманова – М.: Издательство Московского университета, 2006. – 428 с.
7. Ивашковский С. Н. Макроэкономика / С. Н. Ивашковский – М.: Дело – 2002. – 472 с.
ПРИЛОЖЕНИЕ
Приложение 1
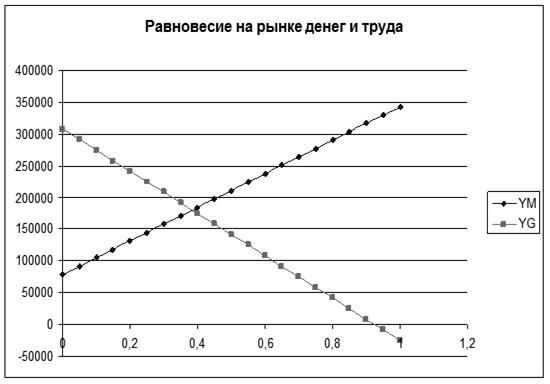
Приложение 2
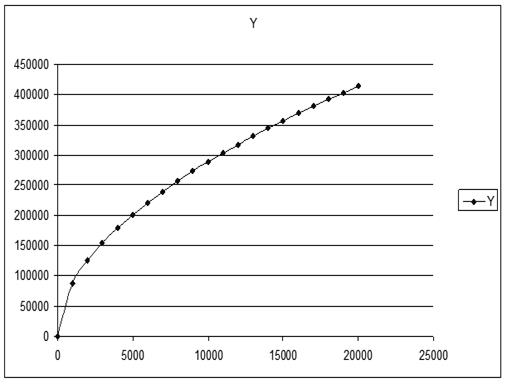
Дата: 2019-05-29, просмотров: 201.
