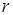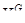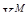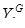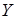Алгоритм вычисления показателей и экономический анализ полученных результатов
В качестве изучаемой системы берётся экономика условного объекта.
Исходные данные приведены в таблице 1:
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
| 127500 | 85000 | 229500 | 0,31 | 11000 | 0,25 | 5100 | 19800 | 0,3 | 2700 | 0,51 |
По заданным в таблице 1 значениям: 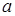 ,
, 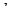 ,
, 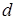 ,
, 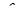 рассчитываем по формуле
рассчитываем по формуле
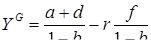 (4.1)
(4.1)
зависимость 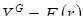 . Значения r задаём в пределах от 0 до 1,0 с шагом
. Значения r задаём в пределах от 0 до 1,0 с шагом 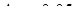 . Результаты вычислений представлены в таблице 2:
. Результаты вычислений представлены в таблице 2:
Таблица 2
|
|
|
| 0 | 307971 |
| 0,05 | 291340,58 |
| 0,1 | 274710,14 |
| 0,15 | 258079,71 |
| 0,2 | 241449,28 |
| 0,25 | 224818,84 |
| 0,3 | 208188,41 |
| 0,35 | 191557,97 |
| 0,4 | 174927,54 |
| 0,45 | 158297,10 |
| 0,5 | 141666,67 |
| 0,55 | 125036,23 |
| 0,6 | 108405,80 |
| 0,65 | 91775,36 |
| 0,7 | 75144,93 |
| 0,75 | 58514,49 |
| 0,8 | 41884,06 |
| 0,85 | 25253,62 |
| 0,9 | 8623,19 |
| 0,95 | -8007,25 |
| 1 | -24637,68 |
Аналогично производим расчёты значений функции 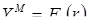 , используя формулу
, используя формулу
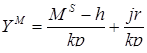 (4.2)
(4.2)
Численные значения 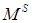 ,
, 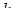 ,
, 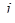 ,
, 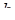 ,
, 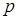 приведены в таблице 1.
приведены в таблице 1.
Результаты вычислений приведены в таблице 3:
Таблица 3
|
|
| 0 | 78666,67 |
| 0,05 | 91866,67 |
| 0,1 | 105066,67 |
| 0,15 | 118266,67 |
| 0,2 | 131466,67 |
| 0,25 | 144666,67 |
| 0,3 | 157866,67 |
| 0,35 | 171066,67 |
| 0,4 | 184266,67 |
| 0,45 | 197466,67 |
| 0,5 | 210666,67 |
| 0,55 | 223866,67 |
| 0,6 | 237066,67 |
| 0,65 | 250266,67 |
| 0,7 | 263466,67 |
| 0,75 | 276666,67 |
| 0,8 | 289866,67 |
| 0,85 | 303066,67 |
| 0,9 | 316266,67 |
| 0,95 | 329466,67 |
| 1 | 342666,67 |
По полученным данным строим графики зависимостей 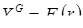 и
и 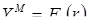 (Приложение 1). По точке пересечения этих графиков находим величины
(Приложение 1). По точке пересечения этих графиков находим величины 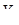 и
и 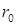 , определяющие равновесие на рынках денег и товаров:
, определяющие равновесие на рынках денег и товаров:
|
| 0,4 |
|
| 184266,67 |
Исходя из условия равновесия на рынках денег и товаров, определяем аналитическим путём величину 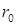 по формуле:
по формуле:
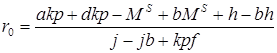 (4.3)
(4.3)
получаем: 
Сравнивая полученное значение 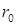 со значением
со значением 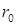 , найденным графическим путем, делаем вывод, что они совпадают. Подставляем значение
, найденным графическим путем, делаем вывод, что они совпадают. Подставляем значение 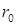 в формулы (4.1) и (4.2) и находим аналитическое значение
в формулы (4.1) и (4.2) и находим аналитическое значение 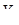 . Аналитическое значение
. Аналитическое значение 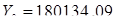 . Сравнивая его с
. Сравнивая его с 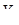 , полученным графическим путем, делаем вывод, что они практически совпадают.
, полученным графическим путем, делаем вывод, что они практически совпадают.
Используя производственную функцию вида:
 (4.4)
(4.4)
находим величину 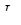 по формуле:
по формуле:
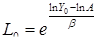 (4.5)
(4.5)
Значения величин 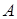 и
и  берём из таблицы 1. По формуле (4.5) получаем:
берём из таблицы 1. По формуле (4.5) получаем: 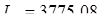 .
.
Рассчитываем по формуле (4.4) производственную функцию 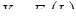 и строим её график (Приложение 2). Результаты вычислений приведены в таблице 4:
и строим её график (Приложение 2). Результаты вычислений приведены в таблице 4:
Таблица 4
|
|
|
| 0 | 0 |
| 1000 | 87138,73 |
| 2000 | 124953,04 |
| 3000 | 154281,66 |
| 4000 | 179177,07 |
| 5000 | 201222,08 |
| 6000 | 221232,99 |
| 7000 | 239696,79 |
| 8000 | 256931,9 |
| 9000 | 273160,15 |
| 10000 | 288543,46 |
| 11000 | 303204,36 |
| 12000 | 317238,21 |
| 13000 | 330721,01 |
| 14000 | 343714,47 |
| 15000 | 356269,54 |
| 16000 | 368428,85 |
| 17000 | 380228,51 |
| 18000 | 391699,43 |
| 19000 | 402868,32 |
| 20000 | 413758,41 |
По значению Y0 находим графическим путем величину L0. Графическое значение L0 = 3775,08. Сравнивая его со значением L0, полученным аналитически, делаем вывод, что они совпадают.
Определение параметров модели
Необходимо определить в простой кейнсианской модели формирования доходов параметры уравнения функции потребления. Исходная система уравнений имеет вид:
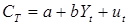 (4.6)
(4.6)
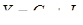 (4.7)
(4.7)
где 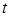 - индекс, указывающий на то, что уравнения (4.6), (4.7) являются системой одновременных уравнений для моментов времени
- индекс, указывающий на то, что уравнения (4.6), (4.7) являются системой одновременных уравнений для моментов времени 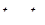 ,
,  - случайная составляющая,
- случайная составляющая, 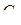 ,
, 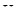 - функции потребления и дохода, соответственно являющиеся эндогенными переменными,
- функции потребления и дохода, соответственно являющиеся эндогенными переменными, 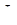 - экзогенно заданная функция, отражающая инвестиционный спрос.
- экзогенно заданная функция, отражающая инвестиционный спрос.
Переменные 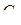 и
и 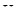 являются эндогенными. Эндогенной считается та переменная, значение которой определяется внутри уравнения регрессии, внутри модели. В качестве экзогенной переменной в данной задаче выступают инвестиции
являются эндогенными. Эндогенной считается та переменная, значение которой определяется внутри уравнения регрессии, внутри модели. В качестве экзогенной переменной в данной задаче выступают инвестиции 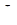 . Экзогенной является та переменная, значение которой определяется вне уравнения регрессии, вне модели и поэтому берется как заданная.
. Экзогенной является та переменная, значение которой определяется вне уравнения регрессии, вне модели и поэтому берется как заданная.
Дата: 2019-05-29, просмотров: 331.