Идеальным газом называется воображаемый газ, молекулы которого представляют собой материальные точки, не имеющие собственного объема и не взаимодействующие между собой. Зависимость между основными термодинамическими параметрами такого газа определяется уравнением состояния идеального газа – уравнением Клапейрона-Менделеева:
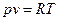, (1)
где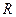 
- газовая постоянная, 
, 
;
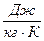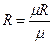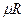- универсальная газовая постоянная,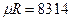 
.
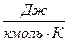Реальные газы состоят из молекул, имеющих конечный собственный объем, между которыми действуют силы межмолекулярного взаимодействия (силы притяжения и отталкивания). Эти газы описываются уравнением (1) только при малых плотностях, когда среднее расстояние между центрами молекул сравнительно велико и эти силы не проявляются. В более плотных реальных газах со значительно меньшим расстоянием между молекулами необходимо учитывать и силы взаимодействия, и собственный объем молекул. Поведение реальных газов качественно отражает уравнение Ван-дер-Ваальса:
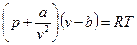, (2)
где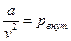 
- внутреннее (молекулярное) давление, возникающее за счет действия сил притяжения и отталкивания между молекулами (для жидкостей оно велико);
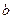- наименьший объем, до которого можно сжать газ, обусловленный собственным объемом молекул.
Тогда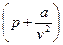 
представляет собой полное давление системы, а 
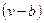– свободный объем.
Для количественных расчетов уравнение (2) часто малопригодно, так как при высоких плотностях, а следовательно, при высоких давлениях параметры, рассчитанные по этому уравнению, расходятся с действительными (экспериментальными) значениями.
Уравнение Ван-дер-Ваальса можно представить в приведенных параметрах состояния. Если переменные p, v и T отнести к их значениям в критической точке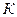 
(далее в опыте Эндрюса эта точка будет рассмотрена подробнее), то можно получить приведенные значения объема 
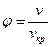, давления 
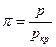и температуры 
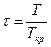и записать так называемое приведенное уравнение состояния:
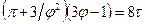. (3)
Состояния веществ, находящихся при одинаковых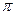 
, 
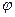и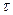 
, называются соответственными состояниями.
Уравнения типа (2) и (3) получаются в случае, если ограничиться рассмотрением только парных взаимодействий между молекулами, т.е. в группах по две молекулы. Поэтому эти уравнения применимы в области не очень высоких давлений.
С повышением давления необходимо учитывать образование устойчивых молекулярных ассоциаций из трех, четырех и более молекул, распад которых возможен только при подводе энергии извне, т.е. при нагревании. Такой газ можно рассматривать как «смесь» нескольких газов, частицами которых являются одиночные, двойные, тройные и т.д. группы молекул [4, 5].
Уравнение состояния реальных газов формально можно записать в виде
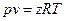, (4)
где z - коэффициент сжимаемости или неидеальности (для идеальных газов z = 1). Коэффициент сжимаемости можно представить в виде вириального уравнения, учитывающего и взаимодействие более высокого порядка:
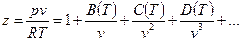. (5)
Правую часть этого уравнения можно рассматривать как разложение в ряд коэффициента z по степеням плотности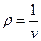 
. Зависящие от температуры функции 
, 
, 
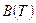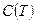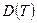, и т.п. выступают здесь как вириальные (от латинского viris - силы) коэффициенты, учитывающие соответственно парные, тройные, четверные и т.д. взаимодействия. Область справедливости вириального разложения ограничивается сходимостью рядов. Ряды расходятся при плотностях, соответствующих жидкому состоянию. Уравнение (5) оказывается справедливым для газов умеренной плотности. Расчеты вириальных коэффициентов достаточно сложны, и поэтому уравнение (5) используется в основном при проведении научных исследований.
Коэффициент неидеальности z может быть найден также по зависимости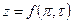 
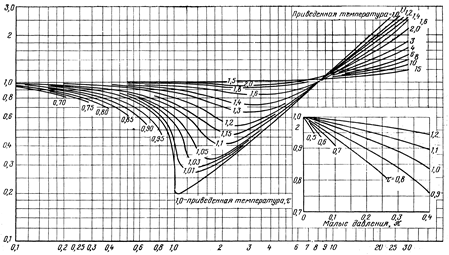
из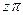 
- диаграммы (рис.1). Рассчитанное значение 
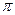откладывается на соответствующей оси этой диаграммы, и из этой точки проводится прямая, перпендикулярная оси 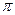, до пересечения с кривой, соответствующей рассчитанному значению t. Точка пересечения позволяет определить искомую величину коэффициента неидеальности на оси z . Точность расчетов в этом случае окажется такой же, как и по уравнению Ван-дер-Ваальса (2) или приведенному уравнению (3).
|
|
Опыт Эндрюса
Свойства реальных газов не только в количественном, но и в качественном отношении отличаются от свойств идеальных газов. Теория идеальных газов не может объяснить фазовые превращения газа и жидкости, она не может установить границы области фазовых переходов, параметры критического состояния.
|
|
|
|
|
|
|
|
|
|
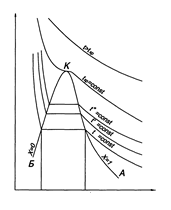
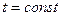) сжатия можно по pv-диаграмме (рис. 2). Участок 1-2 кривой сжатия соответствует изменению параметров p и v газообразного состояния вещества. В точке 2 газ сжимается до объема v”, давление газа достигает величины рн – давления насыщения при данной температуре t, и газ начинает конденсироваться пр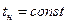и 
и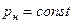 
(процесс 2-3). В точке 3 весь газ переходит в жидкое состояние и занимает объем v’, и процесс конденсации завершается. Кривая 3-4 соответствует процессу сжатия жидкой фазы при 
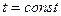. Поскольку жидкость плохо сжимается, объем здесь меняется мало, а давление резко возрастает.
Исследуя зависимость v от р на разных изотермах t, t’, t” и т.д., Эндрюс установил, что, чем выше температура, тем меньше разница между удельными объемами сухого насыщенного пара (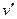 
) и насыщенной жидкости ( 
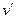). С повышением температуры ( 
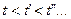) точки 2, 
, 
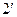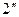…, образующие верхнюю пограничную кривую АК (линия сухого насыщенного пара, x = 1), сближаются соответственно с точками 3, 
, 
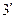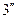…, образующими нижнюю пограничную кривую БК (линия кипящей жидкости, х = 0). Здесь х – степень сухости:
х =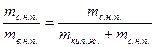 
,
где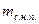 
- масса сухого насыщенного пара;
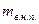- масса влажного насыщенного пара – смеси кипящей жидкости и сухого насыщенного пара.
Разность удельных объемов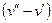 
уменьшается до тех пор, пока при некоторой температуре tкр не станет равной нулю, т.е. 
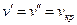. Состояние в точке К с параметрами ркр, vкр и tкр назвали критическим. В этой точке исчезают различия между жидкой и газовой фазами. Поэтому, проводя изотермическое сжатие при различных температурах, можно графически определить положение критической точки.
Таким образом, для реального газа в pv-диаграмме можно выделить пять характерных состояний:
· область жидкого состояния, расположенную левее кривой х = 0 (БК),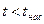 
при данном давлении;
· линию кипящей (насыщенной) жидкости, х = 0 (БК),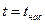 
;
· область влажного насыщенного пара – двухфазное состояние, где пар и жидкость находятся в равновесии и имеют одинаковые рн и tн; она расположена между пограничными кривыми х = 0 и х = 1, т.е. в этой области 0 < x < 1 (между БК и АК),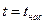 
;
· линию сухого насыщенного пара, х = 1 (АК), ;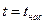
· область перегретого пара, расположенную правее кривой х = 1 (АК),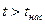 
при данном давлении.
Необходимо отметить, что при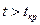 
путем простого изотермического сжатия попасть в область фазовых переходов нельзя. Таким образом, газы, у которых 
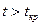, без понижения температуры нельзя перевести в жидкое состояние.
В табл. 1 приведены критические параметры некоторых реальных газов.
Таблица 1
Критические параметры некоторых реальных газов
| Параметры | Н2 | N2 | CO2 | O2 | H2O | Hg |
| t кр., °С | -239,9 | -147,0 | 31,05 | 118,4 | 374,15 | 1480 |
| ркр., МПа | 1,293 | 3,39 | 7,837 | 5,07 | 22,13 | 147,0 |
| v кр., м3/кг | 0,0323 | 0,00322 | 0,002137 | 0,00233 | 0,00326 | - |
Вещество в критическом состоянии характеризуется рядом особенностей. Критическая изотерма tкр. в критической точке К имеет горизонтальную касательную и перегиб, т.е.
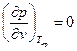и 
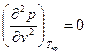. (6)
Вблизи этой точки наблюдается скачок теплоемкости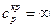 
. В точке К теплота парообразования 
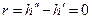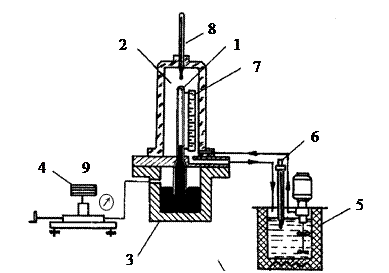
, становятся равными нулю силы поверхностного натяжения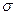 
, которые являются наиболее ярким проявлением межмолекулярного взаимодействия. Поэтому в этой точке отсутствует межфазная поверхность и наблюдается высокая растворяющая способность вещества.
Особые свойства веществ в критической и околокритической областях состояния в настоящее время уже находят применение в пищевой, фармацевтической, парфюмерной, химической, нефтеперерабатывающей отраслях промышленности, в решении экологических проблем. В частности, показано использование суб- и сверхкритических «флюидов» в роли экстрагентов и растворителей в процессах выделения, разделения, очистки и фракционирования [3]. При этом решаются проблемы создания перспективных малоотходных и энергосберегающих технологий.
Проведение опытов
Схема экспериментальной установки представлена на рис. 3. Углекислый газ СО2 находится в толстостенном капилляре 1, выдерживающем давление 7 – 10 МПа. Давление создается масляным прессом 4 и через ртутный затвор передается сжимаемому газу. Постоянство заданной температуры обеспечивается термостатом, подающим воду в прозрачную ячейку 2 из оргстекла, где помещается капилляр 1.
 |
Изменение объема газа при сжатии и происходящая при этом конденсация четко фиксируются по положению границы ртути в капилляре с помощью шкалы на мерной линейке 7. Температура в ячейке измеряется ртутным термометром 8, избыточное давление сжимаемого газа – образцовым манометром 9.
 | |||||
 | |||||
 | |||||
Перед проведением опытов необходимо измерить и записать атмосферное давление В и цену деления шкалы манометра.
Работа выполняется в следующей последовательности:
1. Включить термостат 5. Установить на контактном термометре 6 заданную температуру опыта t1 и дождаться ее стабилизации в измерительной ячейке. Значение этой температуры занести в таблицу (табл.2).
2. С помощью масляного пресса 4 сжать газ до появления мениска ртути в поле зрения капилляра 1. Занести в таблицу (табл.2) показания манометра ризб. (в делениях) и по шкале мерной линейки 7 – высоту газа в капилляре l, мм, пропорциональную сжимаемому объему СО2.
3. Повышать давление (по два деления шкалы манометра с фиксацией высоты газа l) до появления мениска конденсата над ртутным столбиком (точка 2 на рис. 2). Данные занести в таблицу (табл.2), где отметить эту точку как начало процесса конденсации.
Таблица 2
Результаты измерений
| № опытных точек | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
| t1 = , °С | ризб. | делений | |||||||||||||||
| кгс/см2 | |||||||||||||||||
| рабс. | МПа | ||||||||||||||||
| l | мм | ||||||||||||||||
| v | м3/кг | ||||||||||||||||
| В = , мм рт. ст. | Шкала манометра 1 дел = , кгс/см2 | ||||||||||||||||
4. Довести до давления, соответствующего 50 делениям манометра, и перевести вещество в жидкое состояние. Занести в таблицу (табл.2) высоту жидкости l и отметить в таблице эту точку (точка 4 на рис. 2).
5. Посредством масляного пресса понижать давление по 4 деления за опыт, записывая высоту столба жидкости в капилляре. После появления в капилляре газа над жидкостью (точка 3 на рис. 2 – начало парообразования) опыты прекратить.
6. По указанию преподавателя повторить действия п.п. 1-5 при температурах t2 и t3.
7. Показать результаты измерений преподавателю.
Положение точки 3 на pv-диаграмме (рис. 2) также можно определить графическим построением. Она находится на пересечении горизонтальной прямой, проведенной через точку 2, и вертикальной прямой, проведенной через точку 4.
Обработка опытных данных
1. Рассчитать абсолютное давление газа для всех измерений:
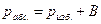, Па;
1 кгс/см2 = 735,6 мм рт. ст.;
750 мм рт. ст. = 105 Па = 0,1 МПа.
При определении ризб. необходимо учитывать цену деления манометра.
2. Удельный объем, равный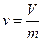 
, м3/кг, из опыта рассчитывается как 
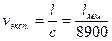, м3/кг,
где V – объем СО2 в капилляре, м3;
m - масса СО2 в капилляре, кг;
l - высота газа в капилляре, мм;
с - постоянная капилляра, с = 8900.
Результаты расчетов p и v занести в таблицу (табл.2).
3. На миллиметровой бумаге построить pv-диаграмму по опытным данным, выбрав масштабы по осям:
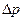= 1МПа 
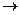2 см;
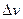= 0,001 м3/кг 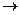1 см.
Используя известные параметры в критической точке К для СО2 (табл. 1), нанести предполагаемые пограничные кривые АК и БК (проведенные через точки 2 и 3) – см. рис. 2. Показать на диаграмме области: жидкого, влажного насыщенного и перегретого состояния вещества, обозначить как кривые кипящей жидкости (х=0) и сухого насыщенного пара (х=1). Показать пунктирными линиями предполагаемую критическую изотерму.
4. Из уравнения (4) рассчитать коэффициент неидеальности z для состояния, указанного преподавателем. Для этой же точки определить коэффициент неидеальности z по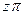 
- диаграмме (рис.1). Сравнить полученные результаты.
5. Рассчитать систематическую погрешность измерений в заданной точке: давления р, барометрического давления В и температуры t:
,
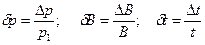где ,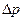 
, 
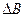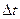- абсолютные погрешности измерения значений р, В и t соответственно.
Подробно материал к этому пункту изложен в разделе «Оценка погрешности эксперимента».
Контрольные вопросы
1. Понятие идеального и реального газа.
2. Уравнения Клапейрона-Менделеева, Ван-дер-Ваальса и приведенное уравнение состояния реальных газов.
3. Коэффициент неидеальности (сжимаемости). 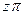-Диаграмма.
4. Опыт Эндрюса. pv-Диаграмма реальных газов. Характер изотерм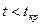 
, 
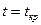и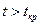 
.
5. Области фазовых состояний вещества. Понятие степени сухости. Характер изменения давления р и температуры t в области фазовых переходов газ - жидкость.
6. Критическая точка, критическое состояние вещества.
7. Особенности критической и околокритической области состояний вещества. Перспективы применения особых свойств этого состояния в промышленности.
8. Экспериментальная установка и результаты опытов.
9. Источники погрешностей измерения. Виды погрешностей. Методика расчета.
Лабораторная работа 24
Дата: 2019-05-29, просмотров: 241.
