При проведении расчетов процессов и аппаратов химической технологии часто необходимо знать количество подведенной или отведенной теплоты. Для их определения используется теплофизическая характеристика – теплоемкость.
Полная теплоемкость – отношение количества теплоты 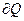 в бесконечно малом термодинамическом процессе к изменению температуры
в бесконечно малом термодинамическом процессе к изменению температуры 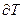 в том же процессе:
в том же процессе:
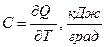 .
.
В практических расчетах используется удельная теплоемкость. Удельной теплоемкостью называется количество теплоты, которое необходимо подвести к единице количества вещества, чтобы изменить его температуру на один градус. В связи с этим определением различают:
- удельную массовую теплоемкость
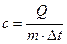 ,
, 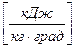 ;
;
- удельную объемную теплоемкость
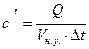 ,
, 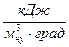 ;
;
- удельную мольную теплоемкость
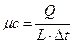 ,
, 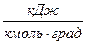 ,
,
где m – масса газа, кг;
Vн.у., 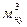 – объем газа, приведенный к нормальным условиям.
– объем газа, приведенный к нормальным условиям.
Приведение объема газа к нормальным условиям связано с тем, что количество вещества (газа) в единице объема зависит от давления р и температуры Т в этом объеме. Чтобы учесть их влияние, объем газа рассчитывают при сопоставимых (например, нормальных) условиях:
( 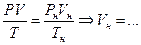 , Рн=760 мм рт. ст.=1,013×105 Па, Тн=273 К);
, Рн=760 мм рт. ст.=1,013×105 Па, Тн=273 К);
L – количество киломолей вещества, кмоль;
L= m/µ,
где  - молекулярная масса газа, кг/кмоль.
- молекулярная масса газа, кг/кмоль.
Тогда расчет теплоты, участвующей в процессе, можно произвести по уравнению
 , кДж, (1)
, кДж, (1)
где х – индекс, указывающий характер процесса подвода теплоты Qx, например при 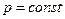 (Qp), при
(Qp), при 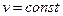 (Qv).
(Qv).
Так как теплота является функцией процесса  , то и теплоемкость также будет зависеть от характера этого же процесса, то есть
, то и теплоемкость также будет зависеть от характера этого же процесса, то есть 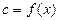 , в связи с чем различают: изобарную теплоемкость ср и изохорную теплоемкость с v.
, в связи с чем различают: изобарную теплоемкость ср и изохорную теплоемкость с v.
Эти теплоемкости для идеальных газов связаны уравнением Майера:
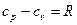 . (2)
. (2)
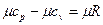 . (2’)
. (2’)
 Теплоемкость зависит от температуры в общем случае нелинейно (рис. 1, линия а):
Теплоемкость зависит от температуры в общем случае нелинейно (рис. 1, линия а):
с Х= a+ bt+ et2+….
 При определении количества теплоты для нагревания от t1 до t2 при
При определении количества теплоты для нагревания от t1 до t2 при  применяют среднюю теплоемкость
применяют среднюю теплоемкость 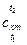 (здесь индекс «m» означает «средний»!), которая при нелинейной зависимости рассчитывается по средним табличным значениям теплоемкостей
(здесь индекс «m» означает «средний»!), которая при нелинейной зависимости рассчитывается по средним табличным значениям теплоемкостей 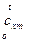 , то есть в интервале температур от 0 до t:
, то есть в интервале температур от 0 до t:
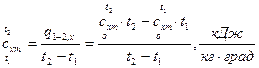 , (3)
, (3)
где  - удельная массовая теплота,
- удельная массовая теплота, 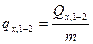 , кДж/кг.
, кДж/кг.
Следовательно,
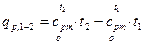 (4)
(4)
или 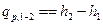 , (4’)
, (4’)
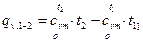 , (5)
, (5)
или  , (5’)
, (5’)
т.е. теплоту можно рассчитать как по значениям теплоемкостией, так и по значениям энтальпии h (при 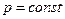 ) и внутренней энергии u (при
) и внутренней энергии u (при 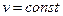 ). Значения
). Значения 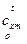 , u и h приводятся в справочной литературе в виде таблиц [1, 2].
, u и h приводятся в справочной литературе в виде таблиц [1, 2].
При уменьшении интервала температур в выражении (3) получим теплоемкость при заданной температуре t, называемую истинной теплоемкостью, сх,ист:
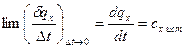 . (6)
. (6)
Со средней теплоемкостью она связана соотношением
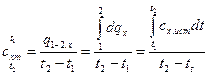 ,
, 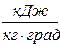 . (7)
. (7)
Для приближенных расчетов можно учесть линейную зависимость теплоемкости от температуры (рис. 1, линия б):
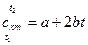 , (8)
, (8)
где a и b – индивидуальные для каждого газа коэффициенты (из таблиц [1]);
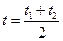 – средняя температура газа.
– средняя температура газа.
Из молекулярно-кинетической теории известно, что энергия, подведенная к системе, состоящей из множества частиц (молекул), распределяется равномерно по степеням свободы i этих частиц. Эта энергия в виде внутренней энергии в идеальном газе распределяется пропорционально степеням свободы поступательного и вращательного движения молекул.
Одноатомная молекула совершает только поступательное движение, то есть изменяется положение молекулы в координатах x, y и z и число степеней свободы i = 3. Для двухатомной молекулы к трем степеням свободы поступательного движения добавляются две степени свободы вращательного движения вокруг атомов: i = 3+2 = 5. Для трех- и многоатомных газов число степеней свободы принимается равным i =3+3+1= 7 (три степени свободы в поступательного движения, три степени свободы вращательного движения и одна степень свободы, учитывающая внутримолекулярное движение атомов и силы взаимодействия между молекулами). В соответствии с этой теорией для идеальных газов (для реальных газов – при не очень высоких температурах на каждую степень свободы и 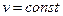 расходуется энергия
расходуется энергия 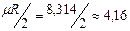 кДж/(кмоль×град). Поэтому постоянные, то есть не зависящие от температуры, мольные теплоемкости
кДж/(кмоль×град). Поэтому постоянные, то есть не зависящие от температуры, мольные теплоемкости  (рис.1, линия в) можно определить в зависимости от атомности газа, по числам степеней свободы i, а
(рис.1, линия в) можно определить в зависимости от атомности газа, по числам степеней свободы i, а 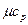 в соответствии с уравнением Майера (2’) - по (i + 2) (табл.1.)
в соответствии с уравнением Майера (2’) - по (i + 2) (табл.1.)
Таблица 1
Значения мольных теплоемкостей в соответствии с молекулярно-кинетической теорией
| Атомность газов | 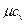 , кДж/(кмоль×град) , кДж/(кмоль×град)
| 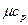 , кДж/(кмоль×град) , кДж/(кмоль×град)
|
| Одноатомные | 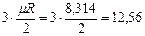
| 
|
| Двухатомные | 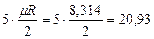
| 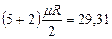
|
| Трех- и многоатомные | 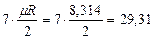
| 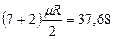
|
Для пересчета различных удельных теплоемкостей удобны соотношения:
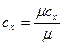 ,
, 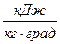 ;
; 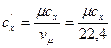 ,
, 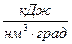 ;
;
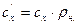 ,
, 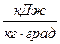 , (9)
, (9)
где 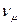 - мольный объем газа при нормальных условиях,
- мольный объем газа при нормальных условиях, 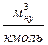 .
.
Определение теплоемкости срт воздуха
методом проточного калориметрирования
Теоретической основой метода является первый закон термодинамики для потока. Расчетное уравнение для определения теплоемкости срт в таком калориметре может быть получено следующим образом. Запишем уравнение первого закона термодинамики для стационарного потока газа с параметрами в сечениях на входе (1) и на выходе (2) из канала:
 , (10)
, (10)
где 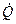 - тепловой поток, т.е. количество теплоты, подведенной электронагревателем в единицу времени, Дж/с или Вт;
- тепловой поток, т.е. количество теплоты, подведенной электронагревателем в единицу времени, Дж/с или Вт;
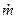 - массовый расход газа, кг/с;
- массовый расход газа, кг/с;
h – энтальпия газа, Дж/кг;
W – скорость газа, м/с;
g – ускорение свободного падения, м/с2;
y – координата сечений 1 и 2 канала по высоте, м.
В данном случае работой, затрачиваемой на изменение кинетической энергии газа 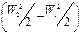 , можно пренебречь, так как скорости газа W1 и W2 мало отличаются друг от друга. Работа, затрачиваемая на изменение потенциальной энергии
, можно пренебречь, так как скорости газа W1 и W2 мало отличаются друг от друга. Работа, затрачиваемая на изменение потенциальной энергии  , равна нулю, поскольку калориметр расположен горизонтально
, равна нулю, поскольку калориметр расположен горизонтально 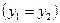 .
.
Таким образом, уравнение (10) принимает вид
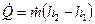 . (11)
. (11)
Проинтегрировав известное выражение для идеального газа
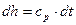 (12)
(12)
в интервале температур от t1 до t2, получим
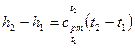 , (13)
, (13)
где 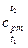 - средняя теплоемкость при
- средняя теплоемкость при 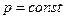 в интервале
в интервале
температур от t1 до t2.
Из уравнений (11) и (13) следует
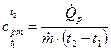 . (14)
. (14)
В проточном калориметре (рис. 2) к потоку газа подводится теплота от электронагревателя и измеряются все величины, необходимые для расчета теплоемкости: расход газа, количество подведенной теплоты, температура газа на входе в калориметр и на выходе из него.
Проведение опытов
1. Включить установку (рис. 2).
2. Установить заданные значения силы тока и расхода воздуха с помощью трансформаторов 5 и 8.
3. После включения установки, в которой исследуются тепловые процессы, требуется некоторое время, в течение которого происходит стабилизация измеряемых величин. Нестационарный период прогревания элементов установки постепенно сменяется стационарным, и измеряемые величины становятся достоверными. На графике стационарности (рис. 3) через каждые 2 мин наносить показания милливольтметра е, мВ, до наступления стационарного режима, при котором вся подводимая теплота идет на нагрев воздуха.

|
|
1 – проточный калориметр, изготовленный из стекла; 2 – вакуумированная оболочка, предназначенная для уменьшения потерь тепла в окружающую среду; 3 – электронагреватель; 4 – дифференциальная термопара, 5,8 – лабораторные автотрансформаторы; 6 – стабилизатор напряжения; 7 – переключатель; 9 – милливольтметр; 10 – вольтметр; 11 – амперметр; 12 – вентилятор; 13 – ротаметр
|
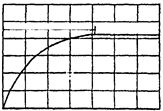 Нестаци. режим стац.режим
Нестаци. режим стац.режим
|
Рис.3. График стационарности
(пример)
Таблица 2
Результаты измерений
| Прот. делений | 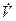 , м3/с , м3/с
| I, A | U эл, В | е , мВ |  , °С , °С
| t 1, °С | t 2, °С | B, мм рт ст. | р=В, Па |
Примечание: Прот. – показания ротаметра; 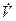 - объемный расход (определяется по градуировочному графику); I – сила тока в электронагревателе (показания амперметра); Uэл – падение напряжения на электронагревателе (показания вольтметра); е – термоЭДС (показания милливольтметра);
- объемный расход (определяется по градуировочному графику); I – сила тока в электронагревателе (показания амперметра); Uэл – падение напряжения на электронагревателе (показания вольтметра); е – термоЭДС (показания милливольтметра); 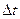 = t2 - t1 - изменение температуры газа в калориметре (определяется по градуировочному графику в зависимости от термоЭДС); В – барометрическое давление, р – давление газа, равное атмосферному, т.е. барометрическому давлению, р=В.
= t2 - t1 - изменение температуры газа в калориметре (определяется по градуировочному графику в зависимости от термоЭДС); В – барометрическое давление, р – давление газа, равное атмосферному, т.е. барометрическому давлению, р=В.
Обработка опытных данных
1. Рассчитать значения теплоемкости и некоторые характеристики процесса. Результаты занести в таблицу обработки опытных данных (табл. 3).
2. Определить теплоемкости с v и с p воздуха, используя молекулярно-кинетическую теорию газов (табл. 1) и соотношения (9).
Вычислить расхождения с экспериментальными данными:
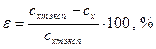 .
.
3. Рассчитать систематическую погрешность измерений при экспериментальном определении срт:
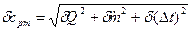 .
.
Подробно материал к этому пункту изложен в разделе «Оценка погрешности эксперимента».
Таблица 3
Обработка экспериментальных данных
| Расчетная величина | Формула | Значение |
| Тепловой поток, выделяемый электронагревателем | 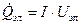 , Дж/с , Дж/с
| |
| Массовый расход входящего воздуха | 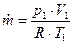 , кг/с, где р1=В , кг/с, где р1=В
| |
| Средняя массовая изобарная теплоемкость воздуха в интервале t 1 – t 2 по уравнению (14) | 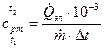 , кДж/(кг×град) , кДж/(кг×град)
| |
| Средняя массовая изохорная теплоемкость воздуха в интервале t 1 – t 2 по уравнению (2) | 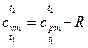 , кДж/(кг×град) где , кДж/(кг×град) где 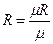 , кДж/(кг×град) , кДж/(кг×град)
| |
| Изменение внутренней энергии | 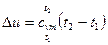 , кДж/кг , кДж/кг
| |
| Изменение энтальпии | 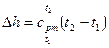 , кДж/кг , кДж/кг
| |
Изменение энтропии в процессе при 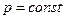
| 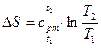 , кДж/(кг×град) , кДж/(кг×град)
| |
Изменение энтропии в процессе при 
|  , кДж/(кг×град) , кДж/(кг×град)
| |
| Показатель адиабаты | 
|
Контрольные вопросы
1. Удельная теплоемкость газов. Определение, обозначения и размерности. Использование удельной теплоемкости для расчетов Qx.
2. Зависимость теплоемкости от характера процесса подвода теплоты. Уравнение Майера.
3. Зависимость теплоемкости от температуры. Понятие средней теплоемкости.
4. Сущность метода проточного калориметрирования. Схема экспериментальной установки.
5. Первый закон термодинамики для потока газа. Расчетное выражение для определения теплоемкости.
6. Методика расчета 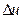 ,
, 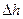 и
и 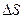 .
.
7. Элементы молекулярно-кинетической теории теплоемкости.
8. Понятие истинной теплоемкости и ее связь со средней теплоемкостью.
9. Техника проведения теплотехнического эксперимента. Понятие стационарного режима.
10. Расчет теплоты для нагревания газа для заданных массы, объема и числа молей на Δ t при С= f( t) нелинейно, линейно и C= const.
Лабораторная работа 23
Дата: 2019-05-29, просмотров: 489.