Сущность статистического метода исследования точности обработки можно пояснит следующим образом. Если на оси Х (рис 5.1) отложить в соответствующем масштабе максимальные размеры измеряемых деталей, а по вертикали частность или количество появления деталей данного размера, то размер каждой порядковой детали в виде точки расположится в поле ∆ рассеивания размеров. Выбрав количество интервалов К, можно разбить поле рассеивания ∆ на ряд интервалов ∆X размеров

.

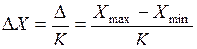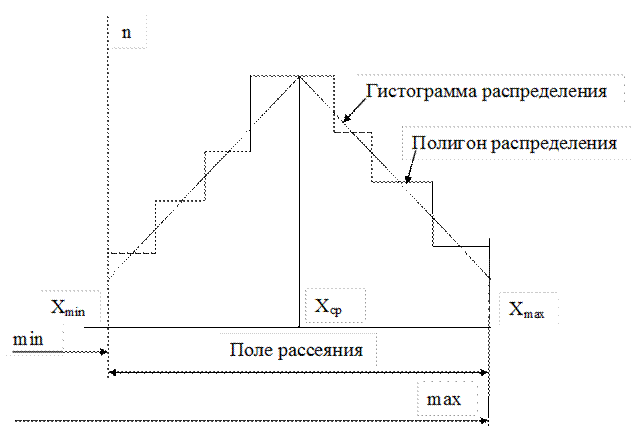Рис. 5.1 Гистограмма и полигон распределения

Числовое выражение количества деталей m, попадающих в каждый интервал или их частность показания , позволит построить ступенчатую диаграмму или гистограмму рассеивания. Соединив середины отдельных столбцов прямыми линиями, получим так называемую кривую рассеивания или полигон распределения. Площадь под кривой (если по оси «y» отложены значения m) определяет в известном масштабе число n измеренных размеров:

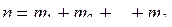
При бесконечном количестве интервалов вместо ступенчатой, получаем плавную кривую распределения, которая в известных случаях может быть выражена математически 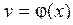. Уравнение, которому подчиняется эта кривая, называется законом распределения. Основными характеристиками погрешности в подобных случаях являются: положение центра группирования или среднее значение, которое определяет центр, относительно которого происходит группирование отклонений.

Для дискретных величин при общем количестве измеренных величин n, если значению интервала X_i соответствует количество деталей данного интервала m_i, то частость значения X_i выражается в долях, как 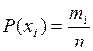, а среднее значение X _ср будет суммой всех частостей

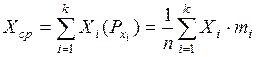
Для непрерывных величин

,

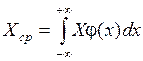где 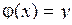 – частота, отвечающая значению x.

Второй, основной характеристикой закона распределения, является дисперсия или мера рассеивания случайной величины относительно центра группирования или центра рассеивания X _ср – это среднее квадратичное отклонение s от среднего значения X _ср.

Для дискретных величин: 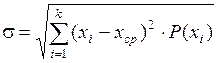 или 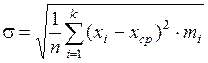, а для непрерывных величин: .

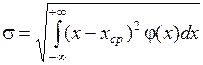Кривые распределения практически имеют различный вид, и вывод математических зависимостей для них может оказаться чрезвычайно сложным. Однако наиболее часто встречается и используется теоретический закон «нормального распределения». Эта закономерность изображается кривой распределения Гаусса, у которой начало координат совпадает с осью симметрии кривой. Уравнение кривой Гаусса имеет вид

,

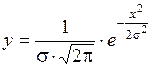где y – частота соответствующая значению x; s – среднеквадратическое отклонение, являющееся абсциссой точки перегиба кривой Гаусса.

Кривая Гаусса, простираясь в обе стороны в бесконечность, асимптотически приближается к оси абсцисс и симметрична относительно начала координат. При х=0 ордината получает максимальное значение

Кривая имеет две точки перегиба при 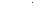. Форма кривой Гаусса определяется значением среднего квадратичного отклонения.

Возможно и несимметричное расположение кривых (рис 5.2).

Рис. 5.2 Пример несимметричного расположения кривой

Величина абсолютной несимметрии m определяется из следующего выражения

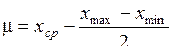
Для графического анализа поля рассеивания и определения степени приближения фактической кривой к теоретической прибегают к построению ее, ограничиваясь четырьмя ординатами: , , .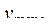

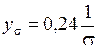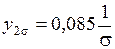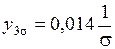Для сопоставления фактической кривой с кривой нормального распределения, необходимо полученные величины привести к одинаковому масштабу, для чего необходимо каждую ординату увеличить на 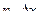, где n – число деталей измеряемой партии,  – величина интервала. Тогда

, , , .

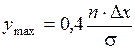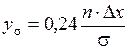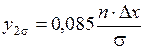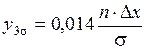Возможны и другие законы распределения погрешностей.

Рассмотрим некоторые из них.

Закон равной вероятности (рис. 5.3) проявляется в том случае, когда при обработке деталей на рассеивание размеров оказывает влияние один доминирующий фактор, например, износ режущего инструмента, с увеличением которого прямо пропорционально изменяется номинальный размер.

Рис. 5.3 Пример расположения кривой, отражающей действие закона равной вероятности

Величина фактического рассеивания размеров определяется по формуле

,

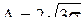где 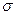 – среднее квадратическое отклонение, определенное, как и для закона нормального распределения.

Закон Симпсона (рис. 5.4) проявляется тогда, когда доминирующая причина в первой половине времени имеет замедленный характер, а во второй – ускоренный, например, недостаточная жесткость системы СПИД.

Это распределение может иметь место при совместном действии размерного износа режущего инструмента с сильно выраженной фазой начального износа и увеличения силы резания в конце стойкости инструмента в результате его прогрессирующего затупления.

В этом случае поле рассеивания определяется по формуле

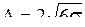
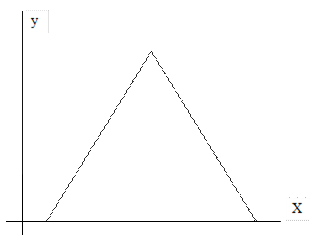
Рис. 5.4 Пример расположения кривой, отражающей действие закона Симпсона

Закон Максвелла (рис. 5.5) проявляется при распределении таких погрешностей обработки, как неточность взаимного положения поверхностей, погрешность формы поверхностей (овальность), ошибка в шаге резьбы и др.

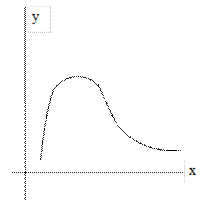
Рис. 5.5 Пример расположения кривой, отражающей действие закона Максвелла

Указанные погрешности являются положительными величинами (они изменяются от нуля до какого-то определенного значения). Поле рассеивания .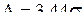

Равномерно возрастающее распределение (рис. 5.6), когда доминирующая причина имеет замедленный характер.

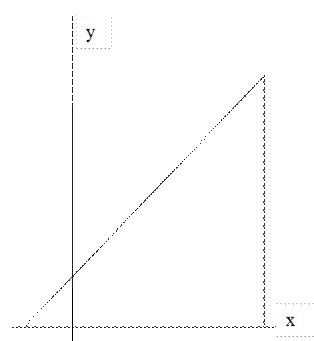
Рис. 5.6 Пример расположения кривой, отражающей равномерно возрастающее распределение

Кривая плотности вероятности отказов в работе (рис. 5.7) собранного изделия или его элемента имеет экспоненциальный характер и выражается уравнением

,

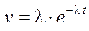где 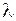– интенсивность отказов.

По оси абсцисс отложено время работы t изделия (наработка на отказ). Вероятность отказа за время t₁ равна площади под кривой в интервале от 0 до t₁ (заштрихованный участок). Кривая характеризует надежность изделия.

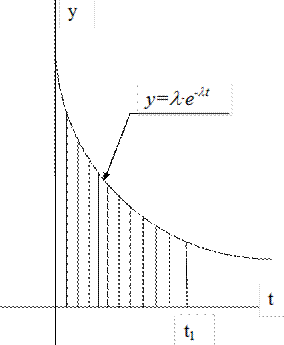
Рис. 5.7 Кривая плотности вероятности отказов в работе

Некоторые композиции законов распределения.

Композиция закона Гаусса и закона равной вероятности (рис. 5.8) – проявляется при совокупном влиянии случайных факторов и одного доминирующего.

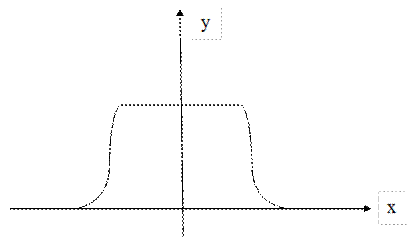
Рис. 5.8 Композиция закона Гаусса и закона равной вероятности

Композиция закона Гаусса и равномерно возрастающего распределения – когда сказывается совокупное влияние случайных факторов и одного доминирующего, имеющего замедленный характер.

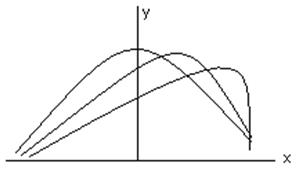
Рис. 5.9 Композиция закона Гаусса и равномерно возрастающего распределения

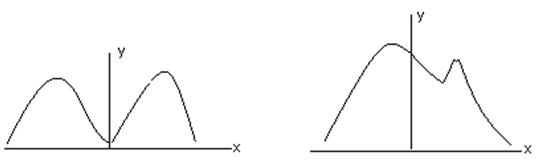
При смешении двух и более партий, в каждой из которых распределение подчиняется закону нормального распределения, итоговое распределение может принять один из видов, представленных на рис. 5.10.

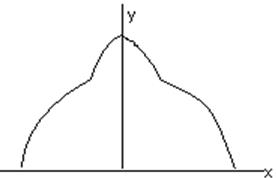
а)

б)                                      в)

Рис. 5.10 Итоговое распределение при смешении:

а) – нескольких партий деталей,

б) – двух равных партий деталей,

в) – двух неравных партий деталей.