1. Энергия системы неподвижных точечных зарядов.

Электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q₁ и Q₂, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда): 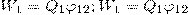где φ₁₂ и φ₂₁ — соответственно потенциалы, которые создаются зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. 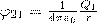Согласно, и поэтому W₁ = W₂ = W и 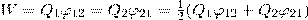Добавляя к нашей системе из двух зарядов последовательно заряды Q₃, Q₄, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна (1) где φ_i — потенциал, который создается в точке, где находится заряд Q_i, всеми зарядами, кроме i-го.

2. Энергия заряженного уединенного проводника.

Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна 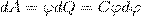");?>" alt="элементарная работа сил электрического поля заряженного проводника"> Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу 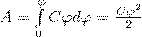(2) Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник: (3) Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем 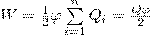где Q=∑Q_i - заряд проводника.

3. Энергия заряженного конденсатора.

Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна 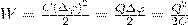(4) где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора. Используя выражение (4), будем искать механическую силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда 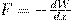(5) Подставив в (4) выражение для емкости плоского конденсатора, получим 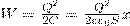(6) Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу: 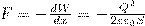где знак минус указывает, что сила F является силой притяжения.

4. Энергия электростатического поля.

Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε₀εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда (7) где V= Sd — объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е. Объемная плотность энергии электростатического поля (энергия единицы объема) 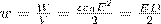(8) Выражение (8) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: Р = æε₀Е.