Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса. Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

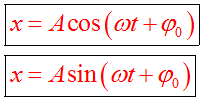
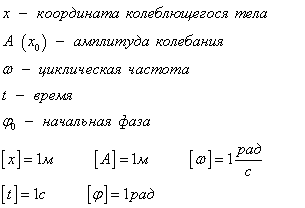
Согласно определению скорости, скорость – это производная от координаты по

Скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.

Величина 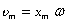- максимальная скорость колебательного движения (амплитуда колебаний скорости).

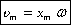
Следовательно, для скорости при гармоническом колебании имеем: ,

а для случая нулевой начальной фазы 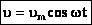(см. график).

Согласно определению ускорения, ускорение – это производная от скорости по времени:

-

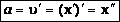вторая производная от координаты по времени. Тогда: .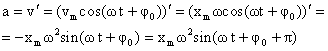

Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения наp(говорят, что колебания происходятв противофазе).

Величина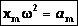

- максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: ,

а для случая нулевой начальной фазы: 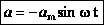(см. график).

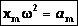
Смещение от положения равновесия при гармонических колебаниях описывается уравнением (его называют кинематическим законом гармонического движения) вида:

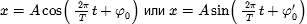
где х — смешение — величина, характеризующая положение колеблющейся точки в момент времени t относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени; А — амплитуда колебаний — максимальное смещение тела из положения равновесия; Т — период колебаний — время совершения одного полного колебания; т.е. наименьший промежуток времени, по истечении которого повторяются значения физических величин, характеризующих колебание; 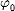— начальная фаза.

14. Математический и физический маятники. Период колебаний. Энергия колебаний.

Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной горизонтальной оси. Точка пересечения ее А вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника (рис. 6.3). Положение тела в каждый момент времени можно характеризовать углом отклонения его из положения равновесия 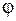. Угол 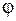играет роль обобщенной координаты q. Кинетическая энергия качающегося физического маятника определяется выражением

,

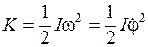где I – момент инерции маятника относительно оси А.

Потенциальная энергия равна

,

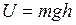где h – высота поднятия центра масс С над его самым нижним положением. Обозначим через а расстояние между центром масс С и точкой подвеса А. Тогда

.

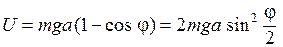В случае малых колебаний синус угла 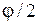можно приближенно заменить самим углом. В этом приближении

.

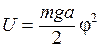Таким образом, для малых колебаний потенциальная и кинетическая энергии приводятся к виду (6.14), причем 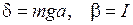. Отсюда следует, что малые колебания физического маятника будут приблизительно гармоническими с циклической частотой

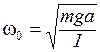(6.18)

и периодом

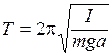. (6.19)

Частным случаем физического маятника является математический маятник. Так называется маятник, вся масса которого практически сосредоточена в одной точке – в центре масс маятника С.

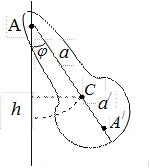
Рис. 6.3

Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае математического маятника

,

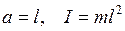где l – длина маятника.

Формула (6.19) переходит в

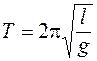. (6.20)

Сравнивая формулы (6.19) и (6.20), заключаем, что физический маятник колеблется так же, как математический маятник с длиной

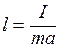, (6.21)

которая называется приведенной длиной физического маятника.

Отложим от точки подвеса А вдоль прямой АС отрезок , длина которого равна приведенной длине физического маятника l (см. рис. 6.3). Точка называется центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.

По теореме Штейнера

,

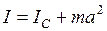где 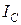– момент инерции маятника относительно параллельной оси, проходящей через центр масс С. Подставив это выражение в формулу (6.21), придадим ей вид

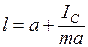. (6.22)

Отсюда следует, во-первых, что l > a, т. е. точка подвеса А и центр качания 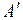лежат по разные стороны от центра масс С и, во-вторых, что всем точкам подвеса, одинаково удаленным от центра масс маятника, соответствует одна и та же приведенная длина l, а следовательно, один и тот же период колебаний T.

Точка подвеса и центр качания являются взаимными или сопряженными точками в следующем смысле. Если маятник подвесить за центр качания 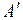, то его период не изменится и прежняя точка подвеса А сделается новым центром качания.