Итак, электростатическое поле можно описать либо с помощью векторной величины 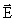, либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:

Изобразим перемещение заряда q по произвольному пути l (Рис. 3.1) в электростатическом поле .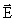

Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl, можно найти так:

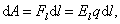
(3.4.1)

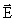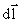где E_l – проекция на ; dl– произвольное направление перемещения заряда.

С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl:

,

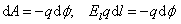отсюда

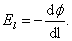
(3.4.2)

Для ориентации dl (направление перемещения) в пространстве, надо знать проекции 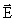на оси координат:

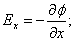
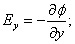
(3.4.3)

По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть

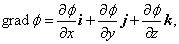
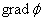– вектор, показывающий направление наибыстрейшего увеличения функции.

Тогда коротко связь между 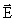и φ записывается так:

(3.4.4)

или так:

,

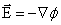(3.4.5)

где (набла) означает символический вектор, называемый оператором Гамильтона.

Знак минус говорит о том, что вектор 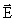направлен в сторону уменьшения потенциала электрического поля.

Направление силовой линии (линии напряженности) в каждой точке совпадает с направлением 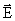. Отсюда следует, что напряженность 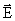равна разности потенциалов U на единицу длины силовой линии.

Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определить 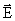между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые линии – прямые. Поэтому здесь определить 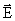наиболее просто:

.

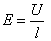(3.6.1)

Теперь дадим определение эквипотенциальной поверхности. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности

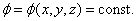
30. Поток вектора напряжённости электрического поля через поверхность. Теорема Гаусса в электростатике.
Как и для любого векторного поля важно рассмотреть свойства потока электрического поля. Поток электрического поля определяется традиционно.

Выделим малую площадку площадью ΔS, ориентация которой задается единичным вектором нормали 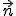(рис. 157).

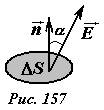
В пределах малой площадки электрическое поле можно считать однородным ^[1], тогда поток вектора напряженности ΔФ_E определяется как произведение площади площадки на нормальную составляющую вектора напряженности

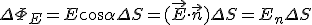. (1)

где 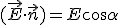— скалярное произведение векторов 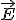и 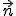; E_n — нормальная к площадке компонента вектора напряженности.

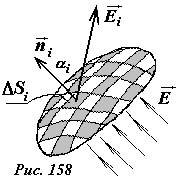
В произвольном электростатическом поле поток вектора напряженности через произвольную поверхность, определяется следующим образом (рис. 158):

- поверхность разбивается на малые площадки ΔS (которые можно считать плоскими);

- определяется вектор напряженности 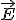на этой площадке (который в пределах площадки можно считать постоянным);

- вычисляется сумма потоков через все площадки, на которые разбита поверхность

.

Эта сумма называется потоком вектора напряженности электрического поля через заданную поверхность.

Теорема Гаусса в интегральной форме. Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

СГС	СИ

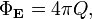
где

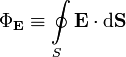§ — поток вектора напряжённости электрического поля через замкнутую поверхность .

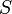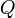§ — полный заряд, содержащийся в объёме, который ограничивает поверхность .

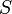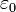§ — электрическая постоянная.

В дифференциальной форме теорема Гаусса выражается следующим образом:

СГС	СИ

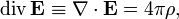
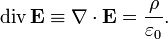
Здесь 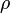— объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла.