Ускорение. Нормальная и тангенциальная составляющие ускорения.

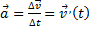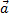Физическая величина, которая определяет быстроту изменения скорости, называется ускорением. Математически ускорение определяется отношением изменения скорости к промежутку времени, за которое оно произошло (производная от скорости по времени): , где – ускорение; 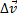– изменение скорости; 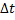– промежуток времени, за которое произошло изменение скорости; 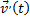– производная скорости по времени.

Так как скорость – величина векторная, то она может меняться по модулю и направлению, поэтому ускорение имеет две естественные составляющие: тангенциальную (параллельную вектору скорости) и нормальную (перпендикулярную вектору скорости).

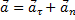, где 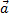– полное ускорение; 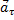– тангенциальная составляющая ускорения; 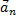– нормальная составляющая ускорения (см. рис. 1).

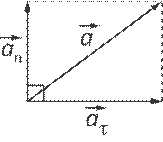
Рис. 1. Тангенциальная и нормальная составляющие полного ускорения

Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости.

1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное (см. рис. 2).

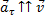
Рис. 2. Тангенциальная составляющая ускорения сонаправлена со скоростью

2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным (см. рис. 3).

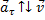
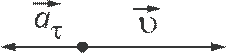
Рис. 3. Тангенциальная составляющая ускорения противонаправлена скорости

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело (см. рис. 4).

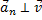
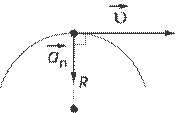
Рис. 4. Направление нормального ускорения

Величина нормального ускорения связана с радиусом траектории и со скоростью движения следующим соотношением: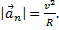

При прямолинейном движении тело имеет только тангенциальное ускорение. Нормальное ускорение отсутствует, так как скорость тела по направлению остаётся неизменной (см. рис. 5).

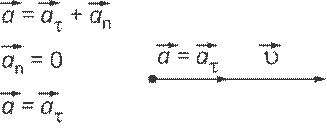
Рис. 5. Прямолинейное движение

При криволинейном движении, как правило, тело имеет тангенциальную и нормальную составляющую ускорения (см. рис. 6).

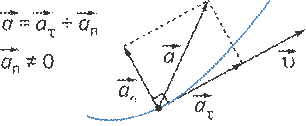
Рис. 6. Криволинейное движение

Закон сохранения импульса

Закон сохранения импульса вытекает из третьего закона Ньютона.

Нужно помнить, что этот закон действует только в замкнутой, или изолированной, физической системе. А замкнутой называют такую систему, в которой тела взаимодействуют только между собой и не взаимодействуют с внешними телами.

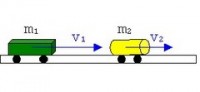
Представим замкнутую систему из двух физических тел. Силы взаимодействия тел друг с другом называют внутренними силами.

Импульс силы для первого тела равен

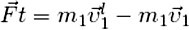
Согласно третьему закону Ньютона силы, которые действуют на тела при их взаимодействии, равны по величине и противоположны по направлению.

Следовательно, для второго тела импульс силы равен

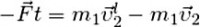
Путём простых вычислений получаем математическое выражение закона сохранения импульса:

,

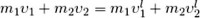где m₁ и m₂ – массы тел,

v₁ и v₂ – скорости первого и второго тел до взаимодействия,

v₁' и v₂' – скорости первого и второго тел после взаимодействия.

_{p1 = m1 · v1} - импульс первого тела до взаимодействия;

_{p2 = m2 · v2} - импульс второго тела до взаимодействия;

p ₁'= m₁ · v₁' - импульс первого тела после взаимодействия;

p₂ '= m₂ · v₂' - импульс второго тела после взаимодействия;

То есть

p₁ + p₂ = p₁' + p₂'

В замкнутой системе тела только обмениваются импульсами. А векторная сумма импульсов этих тел до их взаимодействия равна векторной сумме их импульсов после взаимодействия.

Формула

, где — эффективное сечение молекулы, 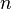— концентрация молекул.

Обозначим эффективный диаметp молекулы чеpез d и молекулу пpедставим как шаp. Тогда число столкновений z молекулы с дpугими молекулами в секунду будет pавно числу молекул, центpы котоpых находятся в цилиндpе длиной, численно pавной <v>, и диаметpом 2d. Это число выpажается формулой


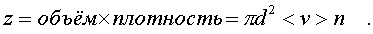
В фоpмулу нужно внести попpавку на то, что данная молекула сталкивается не с неподвижными молекулами, а с движущимися.

Модели в механике: материальная точка и абсолютно твёрдое тело. Система отсчета, радиус-вектор, координаты. Путь и перемещение. Скорость.

Материальная точка – это любое тело, размерами которого можно пренебречь.

Абсолютно твердое тело – такая система материальных точек, в которой расстояние между материальными точками не изменяется, т.е. тело не деформируется ни при каких условиях.

Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системыотсчёта времени, по отношению к которой рассматривается движение каких-либо тел.

Система координат – когда выбрано тело отсчета и через какую-нибудь его точку проводят оси координат и положение любой точки в пространстве описывают ее координатами.

Положение тела или точки можно задать относительно какого-нибудь другого тела, которое называется телом отсчета.

Системы координат бывают различными: прямоугольные и косоугольные, полярные, сферические и другие.

Наиболее часто используется декартова система координат. Это прямоугольная система координат, состоящая из трех взаимно перпендикулярных осей, распределенных в пространстве определенным образом.

Развитие тех или иных процессов в физике происходит с течением времени, т.е. время играет роль параметра (переменной), от которой могут зависеть те или иные физические величины. С точки зрения современной физики и само время может зависеть от тех или иных физических процессов (релятивистская физика). Т.о. мы подошли к тому, чтобы сформулировать основную задачу механики, т.е. ту задачу, которая решается всеми тремя разделами механики.

Эта задача состоит в том, чтобы знать положение тела или точки в любой момент времени, или знать зависимость от времени координат тела или точки. Такая зависимость называется кинематическим законом движения, она может быть записана в виде:

ìx=f1(t)

íy=f2(t) Координатный способ записи. (1.1)

îz=f3(t)

или в виде:

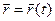Векторная форма записи. (1.2)

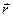- радиус-вектор данной точки.

Можно показать, что эти две формы записи представления кинематического закона движения взаимосвязаны. Для этого необходимо знать, что такое радиус-вектор и как он выражается через координаты.

Радиус-вектор точки – это вектор, проведенный из начала координат в данную точку.

.

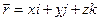Через каждую точку пространства можно провести радиус-вектор. 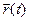- эта формула описывает движение конца вектора в пространстве.

.

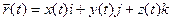Физический смысл - координаты изменяются со временем.

Механическое движение описывается при помощи ряда основных кинематических понятий и величин: траектория, путь, перемещение, скорость, ускорение.

Траектория – линия, которую описывает конец радиус-вектора .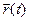

Перемещение тела (материальной точки) - направленный отрезок прямой, соединяющий начальное положение с его последующим движением.

Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка.

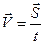, или

Скорость – величина, измеряемая длиной пути, проходимого в единицу времени.

Ускорение – величина, численно равная изменению скорости в единицу времени.

Путь – длина линии, пройденной за время Dt.