5 – «5»
4 – «4»
3 – «3»
2 – «2»
Тема 8
«Начала математического анализа»
1 вариант
А1. Найдите f `(4), если f ( x ) = 4 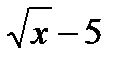 .
.
1) 3; 2)2; 3) -1; 4) 1.
А2. Укажите производную функции 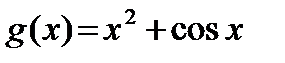 .
.
1)  ; 2)
; 2) 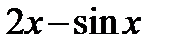 ; 3)
; 3)  ; 4)
; 4)  .
.
А3. Уравнение касательной к графику функции 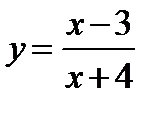 в точке с абсциссой х0 = -3 имеет вид:
в точке с абсциссой х0 = -3 имеет вид:
1) 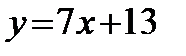 ; 2)
; 2) 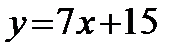 ; 3)
; 3)  ; 4)
; 4)  .
.
А4. Тело движется по прямой так, что расстояние S (в метрах) от него до точки B этой прямой
изменяется по закону 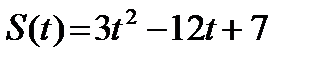 (t – время движения в секундах). Через сколько секунд
(t – время движения в секундах). Через сколько секунд
после начала движения мгновенная скорость тела будет равна 72 м/с.
1) 16; 2)15; 3) 14; 4) 13.
В5. На рисунке изображён график производной некоторой функции 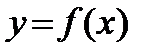 , заданной на
, заданной на
промежутке ( - 3; 3). Сколько точек максимума имеет функция  на этом промежутке?
на этом промежутке?

В6. Найдите угловой коэффициент касательной к графику функции  в точке
в точке 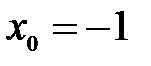 .
.
В7.Найдите производные функций: а) 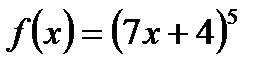 ; б)
; б)  .
.
С8. Найдите сумму тангенсов углов наклона касательных к параболе  в точках
в точках
пересечения параболы с осью абсцисс.
2 вариант
А1. Найдите f `(16), если f ( x ) = 8 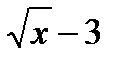 .
.
1) 3; 2)2; 3) -1; 4) 1.
А2. Укажите производную функции 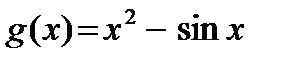 .
.
1) 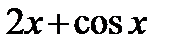 ; 2)
; 2) 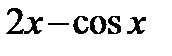 ; 3)
; 3)  ; 4)
; 4)  .
.
А3. Уравнение касательной к графику функции  в точке с абсциссой х0 = -3 имеет вид:
в точке с абсциссой х0 = -3 имеет вид:
1) 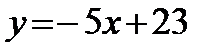 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 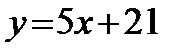 .
.
А4. Тело движется по прямой так, что расстояние от начальной точки изменяется по закону
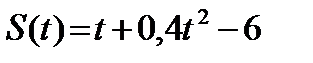 (м), где t – время движения в секундах. Найдите скорость тела через 10
(м), где t – время движения в секундах. Найдите скорость тела через 10
секунд после начала движения .
1) 10; 2)9; 3) 8; 4) 7.
В5. На рисунке изображён график производной некоторой функции 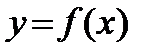 , заданной на
, заданной на
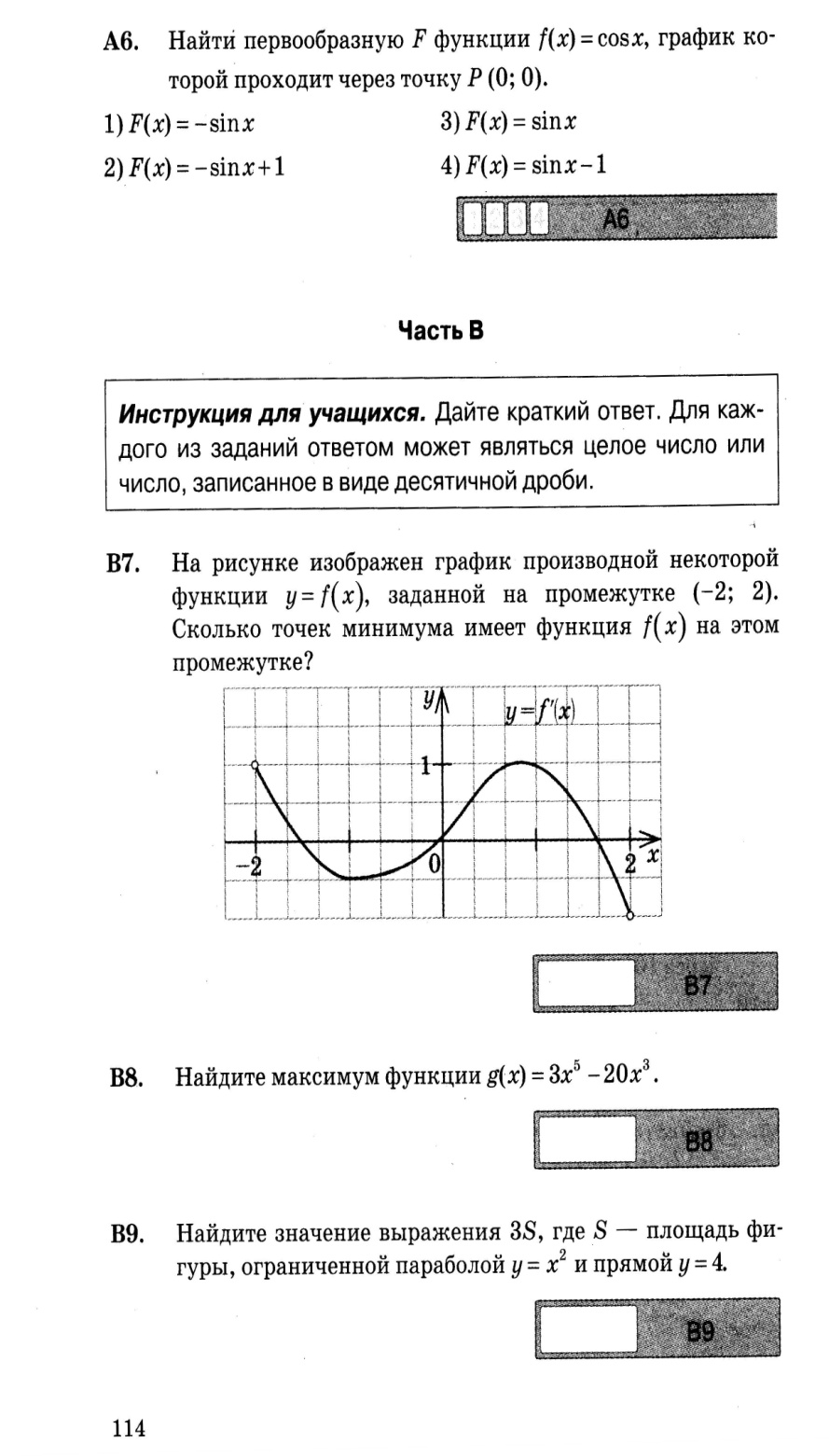
промежутке ( - 2; 2). Сколько точек минимума имеет функция  на этом промежутке?
на этом промежутке?
В6. Найдите угловой коэффициент касательной, проведенной к графику функции  в точке
в точке 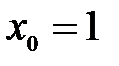 .
.
В7.Найдите производные функций : а) 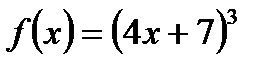 ; б)
; б)  .
.
С8. Найдите сумму угловых коэффициентов касательных к параболе 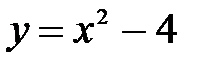 в точках
в точках
пересечения параболы с осью абсцисс.
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 8-9 |
| « 4» (хорошо) | 6-7 |
| « 3» (удовлетворительно) | 5-6 |
| « 2 « (неудовлетворительно) | менее 4 |
Тема 9
«Интеграл и его применение»
1 вариант
А1. . Вычислите интеграл:
а) 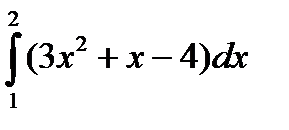 ; б)
; б)  .
.
А2. Для функции f ( x ) = 3sin x найдите:
а) множество всех первообразных;
б) первообразную, график которой проходит через точку М (  ; 0 )
; 0 )
А3. Вычислите, сделав предварительно рисунок, площадь фигуры, ограниченной линиями:
у = 0,5 х2, у = 0, х = 2, х = 0.
А4. Докажите, что функция F является первообразной для функции f ( x ) на промежутке
( - ∞ ; +∞), если F (х) = х3 – 4, f ( x ) = 3х2.
В5. Вычислите интеграл 
С6. Найдите площадь фигуры, ограниченной линиями у = 6х – х2 и у = 2х.
2 вариант
А1. . Вычислите интеграл:
а) 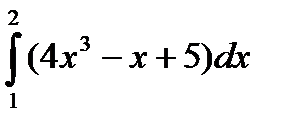 ; б)
; б) 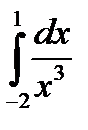 .
.
А2. Для функции f ( x ) = 2cos x найдите:
а) множество всех первообразных;
б) первообразную, график которой проходит через точку М ( 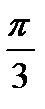 ; 0 )
; 0 )
А3. Вычислите, сделав предварительно рисунок, площадь фигуры, ограниченной линиями:
у = 2 х2, у = 0, х = 3, х = 0.
А4. Докажите, что функция F является первообразной для функции f ( x ) на промежутке
( - ∞ ; +∞), если F (х) = 2х – x2, f ( x ) = 2 - 2х.
В5. Вычислите интеграл 
С6. Найдите площадь фигуры, ограниченной линиями у = - 6х – х2 и у = - 2х.
Рейтинг- 15 баллов.
Дата: 2019-05-28, просмотров: 345.