УЧЕБНОЙ ДИСЦИПЛИНЫ
ОУД.04 . Математика
по программе подготовки специалистов среднего звена
по профессии среднего профессионального образования
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ МАТЕРИАЛЫ ДЛЯ ТЕКУЩЕГО КОНТРОЛЯ УСПЕВАЕМОСТИ ПО ДИСЦИПЛИНЕ ОУД.04 . Математика
Контрольные работы
Тема 1: «Развитие понятия о числе»
Вариант 1
1.Запишите число в стандартном виде:
а)730000000; б)0,0000025;
в)0,24 *10-3; г)75,2*104.
2. Представьте обыкновенную дробь в виде десятичной периодической дроби:
а) 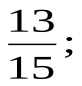 б)
б) 
3. Вычислите:
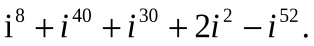
4. Найдите сопряжённое число комплексному числу:
z= 4 + 5i.
5. Обратите чистые периодические десятичные дроби в обыкновенные:
а) 0,(42); б) 0,(513).
6. Обратите смешанные периодические десятичные дроби в обыкновенные дроби:
а) 0,0(27); б) 0,0(01).
7. Даны числа z1= - 1 +3 i, z2= 4 + 5i. Вычислите:
а) модули чисел z1 и z2;
б) сумму чисел z1 и z2;
в) разность чисел z1 и z2;
г) произведение чисел z1 и z2.
8. Постройте комплексные числа в координатной плоскости:
z1= - 1 +3i, z2= 4 + 5i.
9. Найдите значение дроби:
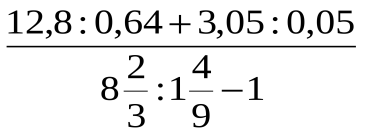
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 9-8 |
| « 4» (хорошо) | 6-7 |
| « 3» (удовлетворительно) | 4-5 |
| « 2 « (неудовлетворительно) | менее 4 |
Вариант 2
1. Запишите число в стандартном виде:
а) 37000000; б)0,00000052;
в) 0,42*10-4; г)52,7*105.
2. Представьте обыкновенную дробь в виде десятичной периодической дроби:
а) 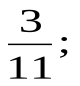 б)
б) 
3. Вычислите:

4. Найдите сопряжённое число комплексному числу:
z= 4 -7i.
5. Обратите чистые периодические десятичные дроби в обыкновенные:
а) 0,(72); б) 0,(918).
6. Обратите смешанные периодические десятичные дроби в обыкновенные дроби:
а) 0,3(6); б) 0,11(6).
7. Даны числа z1= - 3 +5i, z2= 4 -7i. Вычислите:
а) модули чисел z1 и z2 ;
б) сумму чисел z1 и z2;
в) разность чисел z1 и z2;
г) произведение чисел z1 и z2.
8. Постройте комплексные числа в координатной плоскости:
z1= - 3 + 5i, z2= 4 -7i.
9. Найдите значение дроби:
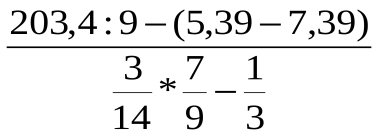
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 9-8 |
| « 4» (хорошо) | 6-7 |
| « 3» (удовлетворительно) | 4-5 |
| « 2 « (неудовлетворительно) | менее 4 |
Вариант 3
1) Найти производные функций.
а) 0,4х5 – 6 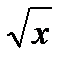 + 3ех
б) 2cos x + + 3ех
б) 2cos x + 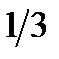 sin x – ln x + 5
в) sin x – ln x + 5
в) 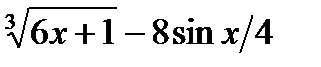 г)
г)  д)
д) 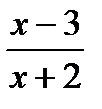
| а) 0,5х4 + 4/х – 3 ln x
б) 3sin x – 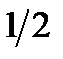 cos x + 2ех – 3
в) cos x + 2ех – 3
в) 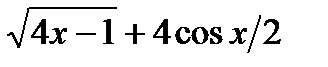 г)
г) 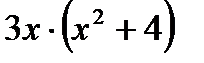 д)
д) 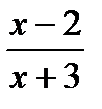
|
2) Решить уравнение f '(х) = 0, если
| а) f (х) = 1/2х + cos(х – п/3) б) f (х) = 2х3 – 3х2 + 1 | а) f (х) = – 1/2х + sin(х – п/6) б) f (х) = х3 + 1,5х2 – 1 |
3) Написать уравнение касательной к графику функции у = f (х) в точке с абсциссой хо, если
| f (х) = х2 + 2х, хо = – 2 | f (х) = х2 – 3х, хо = 3 |
4) Найти f '(х) и f '(0,25), если
f (х) = 
| f (х) = 
|
5) В какой точке графика функции у = 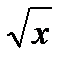 касательная наклонена к оси абсцисс под углом
касательная наклонена к оси абсцисс под углом 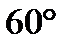 ( 2 в. :
( 2 в. :  )?
)?
6) Найдите острый угол, который образует с осью ординат касательная к графику функции у = f(x) в точке хо, если
f (х) = 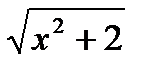 , хо = 1 , хо = 1
| f (х) =  , хо = 3 , хо = 3
|
Дополнительные задания 7) Найти производные функций.
а) cos23х
б) 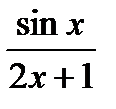 в)
в)  г) ln
г) ln 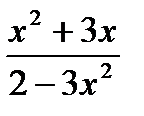 д) (sin х)1/2
е) ln(х2 + 3х)
д) (sin х)1/2
е) ln(х2 + 3х)
| а) sin2х/2
б)  в)
в) 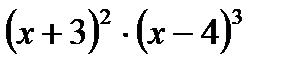 г) ln
г) ln 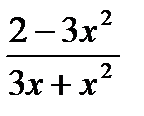 д) cos (1 + ех )
е) cos3х
д) cos (1 + ех )
е) cos3х
| а) 1/2 cos4(2x2 – 3)
б) 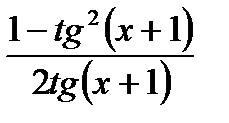 в) – 2 + x2sin x + 2x cos x
г)
в) – 2 + x2sin x + 2x cos x
г) 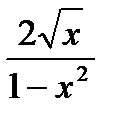 д) sin32x + cos32x
е)
д) sin32x + cos32x
е) 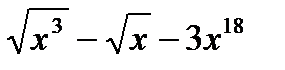
|
8) Написать уравнение касательной к графику функции
у =  , параллельной прямой у = 6х.
, параллельной прямой у = 6х.
9) Написать уравнение касательной к графику функции у = 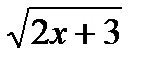 ,
,
проходящей через точку (– 2; 0).
10) Прямая касается гиперболы у = 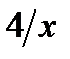 в точке (1; 4) . Найти площадь треугольника, ограниченного этой касательной и осями координат.
в точке (1; 4) . Найти площадь треугольника, ограниченного этой касательной и осями координат.
11*) Написать уравнение общих касательных к графикам функций
а) у = х2 + х и у = х2 – 3х; б) у = х2 и у = х3; в) у = 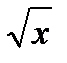 и у =
и у = 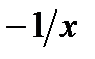 .
.
12*) Записать уравнение прямой, проходящей через точку (1/2; 2), касающейся графика у =  и пересекающей в двух точках график функции у =
и пересекающей в двух точках график функции у = 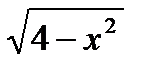 .
.
Вариант № 4* Вариант № 5*
1) Написать уравнение касательной к графику функции у = f (х) в точке
а) у = 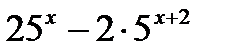 , в (.) еёминимума
б) у = , в (.) еёминимума
б) у = 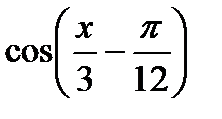 , в (.) с абсц. , в (.) с абсц. 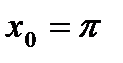
| а) у = 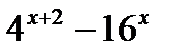 , в (.) её максимума
б) у = , в (.) её максимума
б) у = 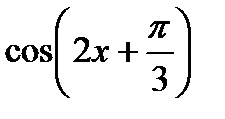 , в (.) с абсц. , в (.) с абсц. 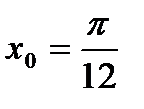
|
2) В каких точках касательная к гр-у функции у1 параллельна прямой у2?
у1 =  , у2 = , у2 = 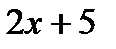
| у1 = 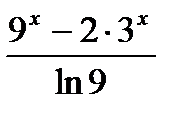 , у2 = , у2 = 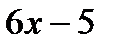
|
3) При каких значениях параметра р касательная, проведённая к графику функции в точке с абсциссой хо, проходит через точку М?
| у = х3 + 2рх, хо = 2, М (1; 2) | у = х3 + рх, хо = – 1, М (3; 2) |
4*) При каких значениях параметров прямые у1 и у2 касаются параболы?
| у1 = 5х – 6, у2 = – х, у = х2 + рх + с | у1 = 2х, у2 = 3х – 2, у = х2 + рх + с |
5) При каких значениях параметра р касательная к графику функции отсекает от 3 четверти ( 2 в. – от 1 четверти) равнобедренный треугольник, площадь которого равна 9/8 ( 2 в. = 25/8 )?
| у = 2р – х2 | у = – р – х2 |
6) При каких значениях параметров график функции у = х3 + рх2 + вх + с касается прямой у = 4х + 4 в точке с абсциссой х = – 1 и пересекает эту прямую в точке с абсциссой х = 2?
7) Хорда параболы у = х2 – 2х + 5 соединяет точки с абсциссами х1 = 1 и х2 = 3. Составить уравнения касательных параллельных хорде.
8) Прямая проходит через точки А(– 4; – 2) и В(0; 1) [ А(4; 6) и В(0; 1) ]. Определите, в какой точке она касается графика функции 
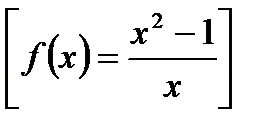 .
.
Вариант 1
1. Вычислить
| - |
| + |
 б.
б.  3 *
3 * 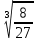
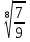 в.
в. 
2. Найдите значение числового выражения:
а.  б.
б. 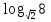 в.
в. 
3. Сравните числа:
а. log153 и log15  б. log 0,15 5 и log 0,15
б. log 0,15 5 и log 0,15  .
.
4. Упростите выражение:
а. 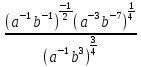 б.
б. 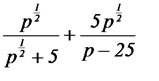
5. Сократить дробь:

6. Упростите выражение:
a . 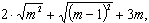 б.
б. 
Вариант 2
1. Вычислить:
| + |
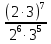 б.
б. 
 в.
в. 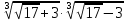
2. Найдите значение числового выражения:
а. 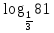 б.
б. 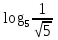 в. log0,25 8
в. log0,25 8
3. Сравните числа:
а. log4 0,3 и log7 2; б. log32 и log1317 .
4. Упростите выражение:
а. 
б. 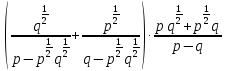
5. Сократить дробь:

6. Упростите выражение:
a . 
б. 
Вариант 3
1. Вычислить:
| - |
| + |
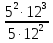 ; б.
; б. 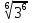
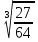 (
(  )0; в.
)0; в. 
2. Найдите значение числового выражения:
а. 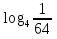 б.
б. 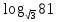 в. log512
в. log512
3. Сравните числа:
а. log4 7 и log4 27; б. log9  и log9 13.
и log9 13.
4. Упростите выражение:
а. 
б. 
5. Сократить дробь:
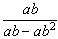
6. Упростите выражение:
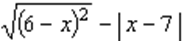
Вариант 4
1. Вычислить:
а. 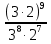 ; б.
; б. 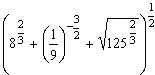 ; в.
; в.  .
.
2. Найдите значение числового выражения:
а.  б.
б. 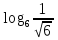 в. 2log 0,01
в. 2log 0,01
3. Сравните числа:
а. log5 3 и  ; б. log4 0,3 и log7 2.
; б. log4 0,3 и log7 2.
4. Упростите выражение:
а. 
б. 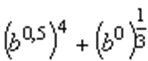 .
.
5. Сократить дробь:
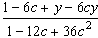
6. Упростите выражение:
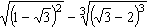
Вариант 5
1. Вычислить:
а. 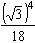 ; б.
; б. 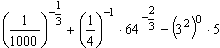 ; в.
; в. 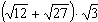 .
.
2. Найдите значение числового выражения:
а. 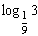 ; б.
; б. 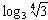 ; в. log232-1.
; в. log232-1.
3. Сравните числа:
а. log 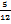 10 и log
10 и log 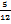 6 б. log2 5 и log2 3
6 б. log2 5 и log2 3
4. Упростите выражение:
а.  ; б.
; б. 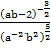
5. Сократить дробь:
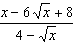
6. Упростите выражение:

Вариант 6
1. Вычислить:
а. 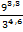 б.
б.  в.
в. 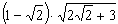
2. Найдите значение числового выражения:
а. log0,25 8; б . 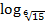 15 ; в. log16
15 ; в. log16 
3. Сравните числа:
а. log2  и log2
и log2  ; б.
; б. 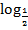 3 и
3 и 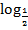 5.
5.
4. Упростите выражение:
а. 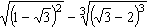 ; б.
; б.  –a+1.
–a+1.
5. Сократить дробь:

6. Упростите выражение:
а. 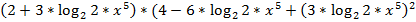
б. 
Вариант 7
1. Вычислить:
а. 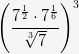 ; б.
; б.  ; в.
; в. 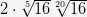 .
.
2. Найдите значение числового выражения:
а.  ; б.
; б.  ; в.
; в. 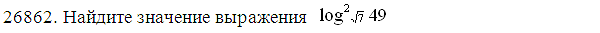 .
.
3. Сравните числа:
а. log3 11 и lg 38; б. log0,23 4 и log0,23  .
.
4. Упростите выражение:
а. 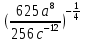 б.
б. 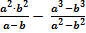
5. Сократить дробь:
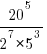
6. Упростите выражение:
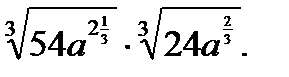
Вариант 8
1. Вычислить:
а. 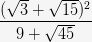 ; б.
; б.  ; в.
; в. 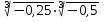 .
.
2. Найдите значение числового выражения:
а.  ; б.
; б. 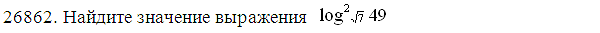 ; в.
; в. 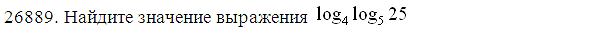 .
.
3. Сравните числа:
а. log4 6 и log6 8; б. log5 3 и  .
.
4. Упростите выражение:
а. 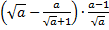
б. 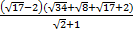
5. Сократить дробь:
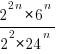
6. Упростите выражение:

Вариант 9
1. Вычислить:
а. 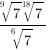 ; б.
; б.  ; в.
; в. 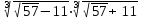 .
.
2. Найдите значение числового выражения:
а. 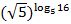 ; б.
; б.  ; в.
; в. 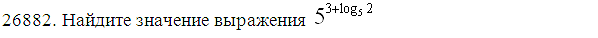 .
.
3. Сравните числа:
а. log4 0,3 и log7 2; б.  4 и
4 и 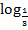 4.
4.
4. Упростите выражение:
а.  ; б.
; б. 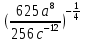 .
.
5. Сократить дробь:

6. Упростите выражение:
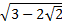
Вариант 10
1. Вычислить:
а. 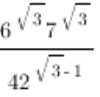 ; б.
; б.  ; в.
; в. 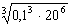 .
.
2. Найдите значение числового выражения:
а. log0,2 125 ; б . log9243 ; в . 
 .
.
3. Сравните числа:
а. 2  и 31log8 35 б. log5 7 и log3 6
и 31log8 35 б. log5 7 и log3 6
4. Упростите выражение:
а.  ; б.
; б. 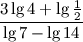 .
.
5. Сократить дробь:

6. Упростите выражение:
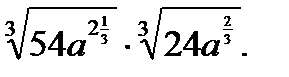
Вариант 11
1. Вычислите:
а. ( 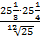 ) б.
) б.  в.
в. 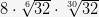
2. Найдите значение числового выражения:
а . log4 32; б . log2 4; в . log4 0,0626.
3. Сравните числа:
а. log20 4 и log80 8; б. 
4. Упростите выражение:
а. 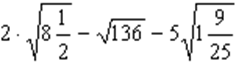 б.
б. 
5. Сократить дробь:
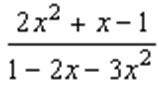
6. Упростите выражение:
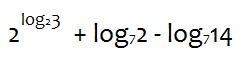
Вариант 12
1. Вычислить:
а. 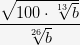 ; б.
; б.  ; в.
; в.  .
.
2. Найдите значение числового выражения:
а. 2 log3 2. б. 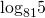 в.
в. 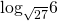
3. Сравните числа:
а. 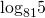 и
и 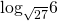 б.
б.  5 и -1
5 и -1
4. Упростите выражение:
а. 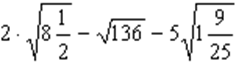 ; б.
; б. 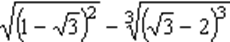 .
.
5. Сократить дробь:
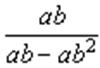
6. Упростите выражение:
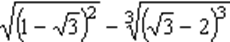
Вариант 13
1. Вычислить:
а. 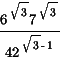 ; б.
; б. 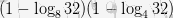 ; в.
; в. 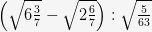 .
.
2. Найдите значение числового выражения:
а. log0,3 10; б . log 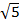 ; в. Log3 12.
; в. Log3 12.
3. Сравните числа:
а.  и
и 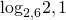 б.
б. 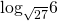 и
и 
4. Упростите выражение:
а. 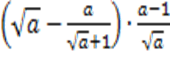 ; б.
; б. 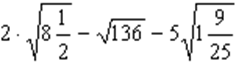 .
.
5. Сократить дробь:
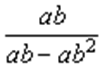
6. Упростите выражение:
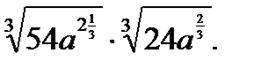
Вариант 14
1. Вычислить:
а. 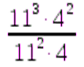 ; б.
; б. 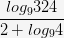 ; в.
; в. 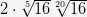 .
.
2. Найдите значение числового выражения:
а . log5 250 ; б . lg 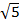 ; в log4 0,125.
; в log4 0,125.
3. Сравните числа:
а.  и
и 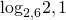 б.
б. 
4. Упростите выражение:
а.  ; б.
; б. 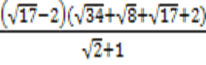 .
.
5. Сократить дробь:

6. Упростите выражение:
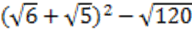
Вариант 15
1. Вычислить:
а.  ; б.
; б. 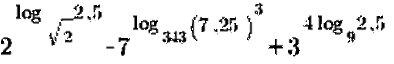 ; в.
; в. 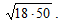
2. Найдите значение числового выражения:
а . log5 250 ; б . lg√5 ; в log4 0,125.
3. Сравните числа:
а. log4 26 и log6 17. б. 2 log3 и log 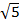
4. Упростите выражение:
а.  ; б.
; б. 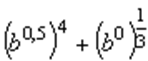 .
.
5. Сократить дробь:
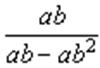
6. Упростите выражение:
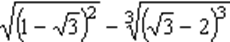
Вариант № 16 Вариант № 17
1) Основание прямоугольного параллелепипеда – квадрат. Сумма длин трёх рёбер, выходящих из одной вершины, равна 6 см. Какое наибольшее значение может иметь объём такого параллелепипеда?
1) Найдите высоту параллелепипеда наибольшего объёма, основание которого – прямоугольник периметра 3 см, а высота равна одной из сторон основания?
2) Исследовать функцию с помощью производной и построить график.
а) у = 6х2 – 2х3
б*) у = 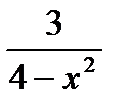
| а) у = 3/2х2 – х3
б*) у = 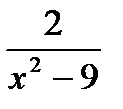
| в*) у = 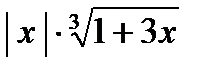 г*) у = г*) у = 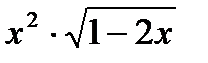 д*)
д*) 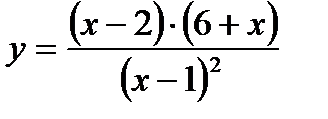 е*) е*) 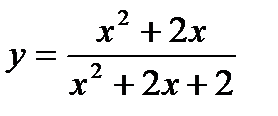
|
3) Найти наименьшее и наибольшее значения функции на промежутке.
а) f (х) = cos х – 1/3cos 3х на [0; п/2]
б*) у = х2 + 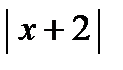 на [– 3; – 1]
в*) у = на [– 3; – 1]
в*) у = 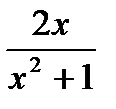 на ООФ на ООФ
| а) f (х) = sin х – 1/3sin 3х на [0; 3п/4]
б*) у =  на [– 1; 3]
в*) у = на [– 1; 3]
в*) у = 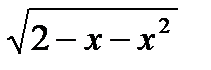 на ООФ на ООФ
|
Вариант № 18* Вариант № 19*
1) Графики – см. задание 2 из вариантов 1 и 2.
2) Найти наименьшее значение функции.
| f (x) = x + log2(2x + 2 – 5 + 2 – x + 2 ) | f (x) = x + log3(3x + 1 – 1 + 3 – x + 1 ) |
3) Найти наименьшее ( 2 в. – наибольшее ) значение выражения.
1 – (cos2 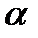 )1/2 – 2 sin2 )1/2 – 2 sin2 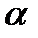
| 1 + (sin2 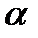 )1/2 + 2 cos2 )1/2 + 2 cos2 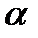
|
4) В фигуру, ограниченную параболой у = 4 – х2 и осью Ох, поместили прямоугольник, две вершины которого лежат на параболе, а две другие - на оси Ох. Найти наибольший из периметров этих прямоугольников.
5) Какую наибольшую площадь может иметь трапеция, три стороны которой равны р?
6) Фигура ограничена параболами у = х2 – 4х – 7 и у = – х2 + 9 . Найти наибольшую из длин отрезков, параллельных оси Оу и лежащих внутри данной фигуры.
7) Фигура ограничена параболой у = х2 и прямой у = 2х + 3 . Найти наибольшую из длин отрезков, параллельных оси Ох и лежащих внутри данной фигуры.
8) Из круга радиуса R вырезан сектор и из сектора склеен конус (боковая поверхность конуса). Каков наибольший объём получившейся конической воронки?
Дополнительные задания
9) Из всех прямоугольных треугольников, у которых сумма одного катета и гипотенузы равна р, найти треугольник с наибольшей площадью. Найти его площадь.
10) Найти МЗФ: 
11*) В какой точке графика функции у = (х – 1)2 , 0 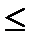 х
х 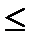 1, надо провести касательную к графику, чтобы площадь треугольника, ограниченного этой касательной и осями координат, была наибольшей?
1, надо провести касательную к графику, чтобы площадь треугольника, ограниченного этой касательной и осями координат, была наибольшей?
12*) На графике у = 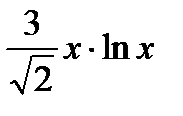 , где
, где 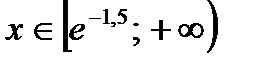 . Найти М (х; у), чтобы отрезок касательной к графику функции в этой точке, заключённый между точкой М и осью Оу, имел наименьшую длину.
. Найти М (х; у), чтобы отрезок касательной к графику функции в этой точке, заключённый между точкой М и осью Оу, имел наименьшую длину.
13*) Найдите кратчайшее расстояние от точки А до графика функции f (х), если А(1; 0), f (х) =  [А(– 3; 0), f (х) =
[А(– 3; 0), f (х) =  ].
].
14*) Исследовать функцию на выпуклость:
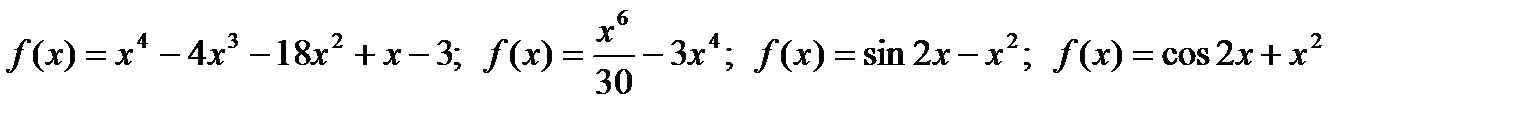
15*) Исследовать функцию с помощью производной и построить график.
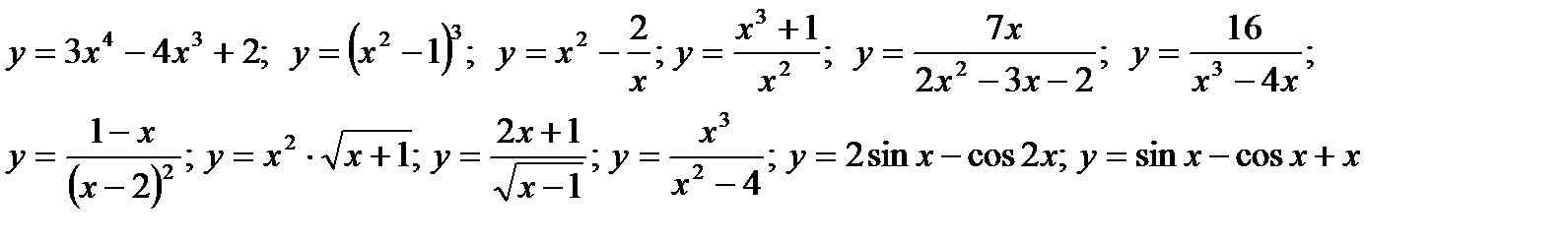
Вариант 1
1. Найдите значение
а) sin 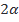 , если sin
, если sin 
б) cos ( 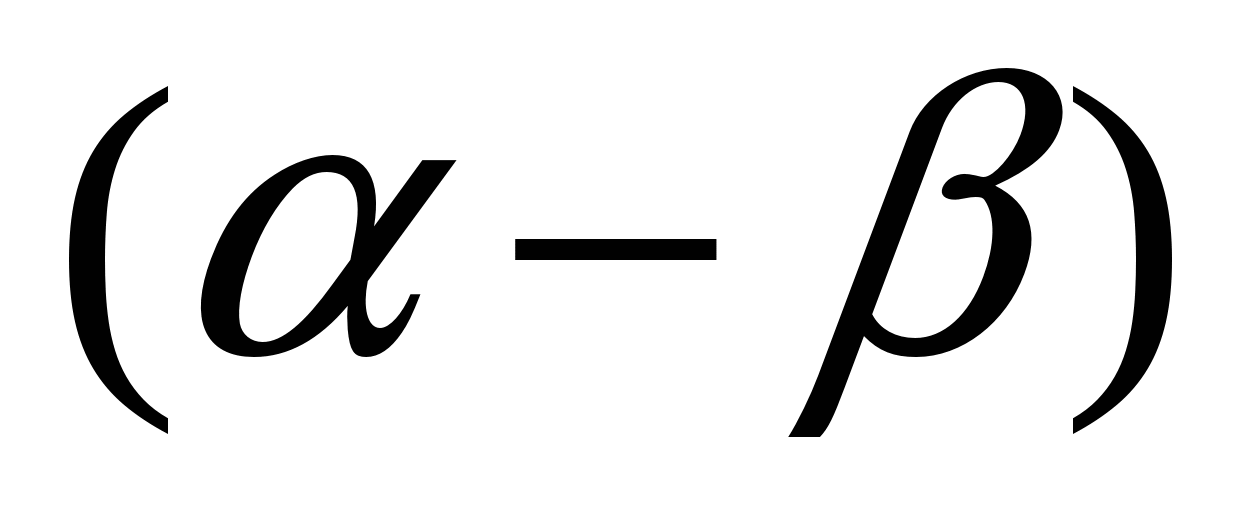 -2sin
-2sin 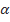 sin
sin  , если
, если 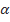 =30°; β=15°
=30°; β=15°
2. Упростите выражение:
а) cos2α+sin2α;
б) 1- 
3. Докажите, что sin40°+cos70°-cos10°=0
4. Представьте в виде произведения sinα- sin 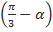
5. Найдите наибольшее и наименьшее значение выражения 5+ cos 
Вариант 2
1. Найдите значение
а) cos 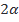 , если cos
, если cos 
б) cos 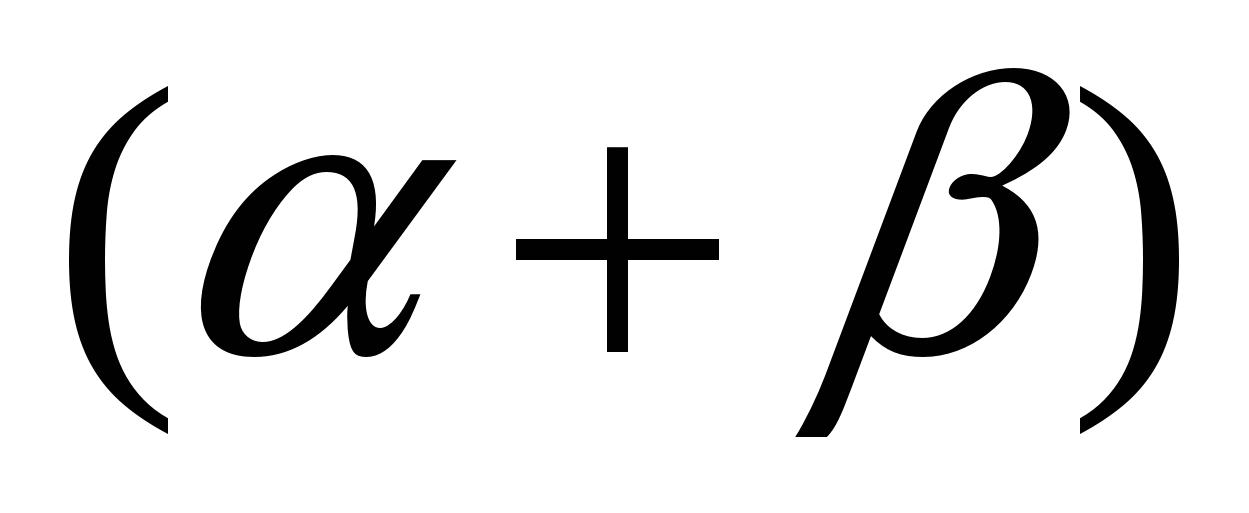 -2sin
-2sin  sin
sin  , если
, если  =75°; β=15°
=75°; β=15°
2. Упростите выражение:
а) cos2α+sin2α;
б) 1- 
3. Докажите, что сos12°+cos48°-sin18°=0
4. Представьте в виде произведения cosα-cos 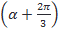
5. Найдите наибольшее и наименьшее значение выражения 5+ sin 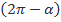
Вариант № 3 Вариант № 4
1) Вычислить площадь фигуры, ограниченной линиями.

| 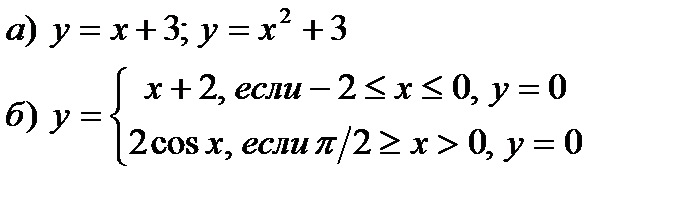
|
2) Вычислить интеграл.
а) 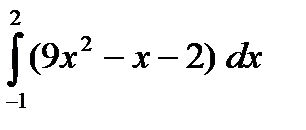 б)
б)  в)
в) 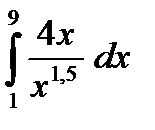 г)
г) 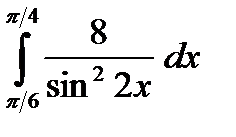 д)
д) 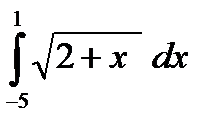
| а)  б)
б)  в)
в) 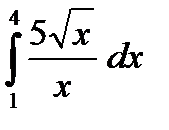 г)
г) 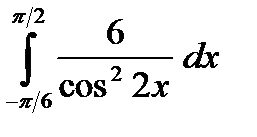 д)
д) 
|
3) Для функции f (x) найти первообразную, график которой проходит через точку М .
а) f (x) =  x2 – 3; M x2 – 3; M 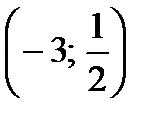 б) f (x) = cos
б) f (x) = cos 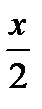 ; M ; M 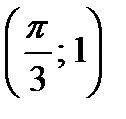
| а) f (x) = 2x2 – x; M 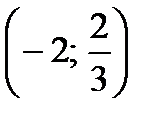 б) f (x) = sin 3x; M
б) f (x) = sin 3x; M 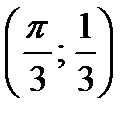
|
Дополнительные задания 4) Найти первообразные функции.
у =  ; у =
; у = 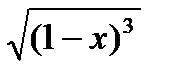 ; у = 2е – 3х + 1; у = 32х ; у = 2– 5х ; у =
; у = 2е – 3х + 1; у = 32х ; у = 2– 5х ; у = 
5) Вычислить интеграл
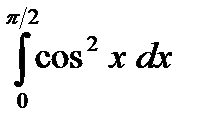 ;
; 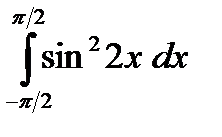 ;
; 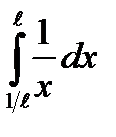 ;
;  ;
; 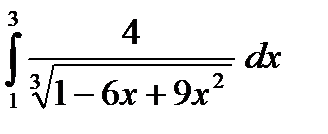 ;
; 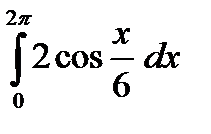 ;
;
 ;
;  ;
;  ;
;  ;
; 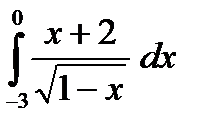 ;
; 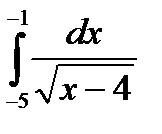
6) Вычислить площадь фигуры, ограниченной линиями,
а) f (x) = ех – 5, х = 0, х = 1 и Ох.
б) f (х) = – 2sin х, х = п, х =  п, у = 0.
п, у = 0.
в) f (х) = sin х/2, х = – п/3, х = п/3, у = 0.
г) f (х) = е 2х – 3, х = – 1, х = 1 и осью абсцисс.
д) f (х) = х2 – 4х + 5, касательной к графику в точке с абсциссой
хо = – 2 и осью ординат.
е) f (х) = sin х, касательной к графику в точке с абсциссой х0 = п и прямой х = п/2.
Вариант № 5* Вариант № 6*
1) Вычислить интеграл.
а) 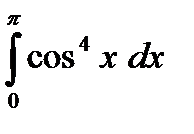 б)
б) 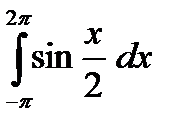 в)
в) 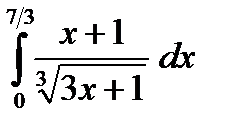 г)
г) 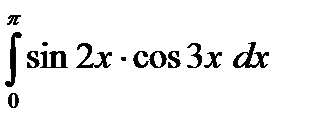 д)
д) 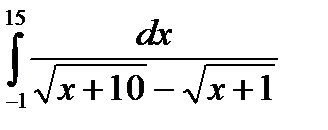 е)
е) 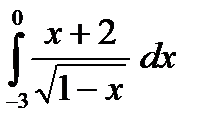 ж)
ж) 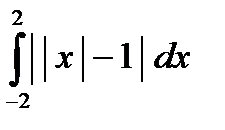 з)
з) 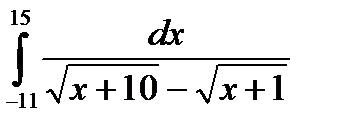
| а) 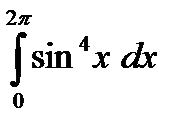 б)
б)  в)
в) 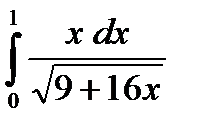 г)
г) 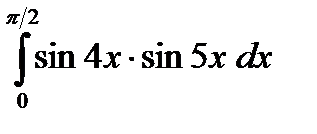 д)
д)  е)
е) 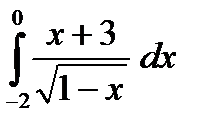 ж)
ж) 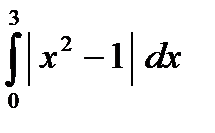 з)
з) 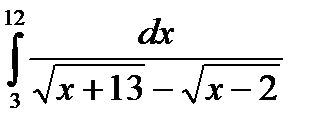
|
2) Найти максимумы ( 2 в. – минимумы ) функции
f (x) = 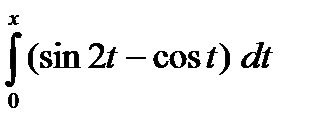 , 0 , 0 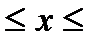 п п
| f (x) = 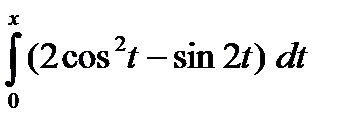 , 0 , 0 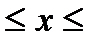 п п
|
3) Вычислить площадь фигуры, ограниченной линиями,
а) Осью Ох, у = 2х2 и касательной к этой кривой в точке с абсциссой равной 2.
б) у = х2 – 4х + 5 и прямыми, касающимися её в точках с абсциссами х1 = 2 и х2 = 4.
в) f (х) = сos х, касательной к графику в точке с абсциссой х0 = 5п/2 и прямой х = 2п.
г) у = 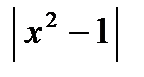 и у = 5 +
и у = 5 +  .
.
д) 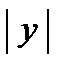 = 2х – х2.
= 2х – х2.
4) Какую часть площади квадрата отсекает парабола, проходящая через две соседние вершины квадрата и касающаяся середины одной из его сторон?
5*) Площадь фигуры, ограниченной линиями у = 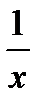 , у =
, у = 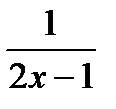 , х = 2,
, х = 2,
х = р, у = 0, равна ln  . Найдите р.
. Найдите р.
6) Найдите те первообразные функции f (x), графики которых
касаются прямой.
| f (x) = x2 – 5x + 3, y = – 3x – 1 | f (x) = x2 – x + 2, y = 2x – 1 |
7) Найти все значения параметра р, для каждого из которых выполняется неравенство.
а)  , р > 0
б) , р > 0
б) 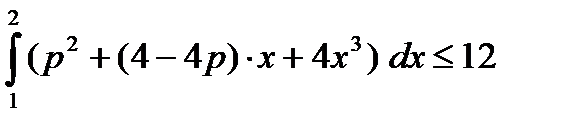
| а)  , р > 1
б) , р > 1
б) 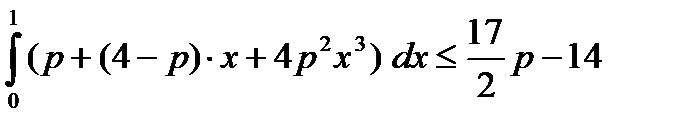
|
8) Найти а) наименьшее, б) наибольшее значение интеграла
а)  б)
б) 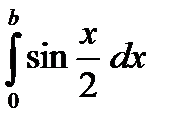
| а) 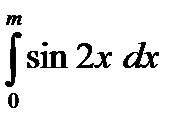 б)
б) 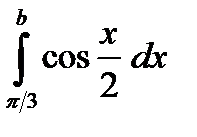
|
9) Для функции f (x) найдите первообразную, обладающую указанными свойствами а) f (x) = 4х + 8 [ f (x) = – х + 3 ] и график первообразной имеет только одну общую точку с прямой у = 3 [ у = 7 ];
б) график первообразной проходит через точки А(1; 10) и В(4; – 2), если  [ А(– 1; 4) и В(3; 4), если
[ А(– 1; 4) и В(3; 4), если 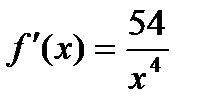 ].
].
Вариант1.
1. Вычисление значений выражений.
№1. Найдите значение выражения:
1) 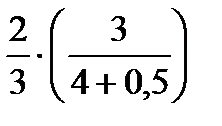 2)
2) 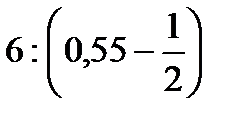 3)
3) 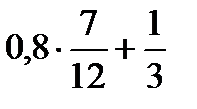 № 2. Вычислить:
№ 2. Вычислить:
1) 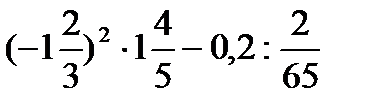
2) 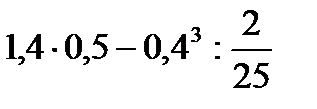
№ 3. Вычислить: 1) 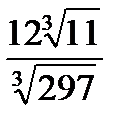 2)
2) 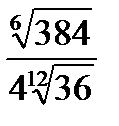
№ 4. Представить в виде степени:
1) 
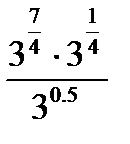 2)
2) 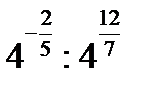
Вариант 2
№1. Найдите значение выражения:
1)  2)
2) 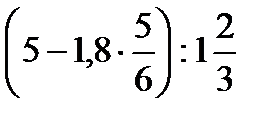 3)
3) 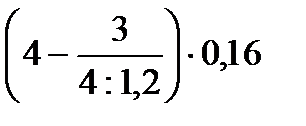
№ 2. Вычислить:
1)  2)
2) 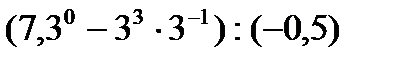

№ 3. Вычислить:
1) 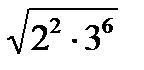
 2)
2) 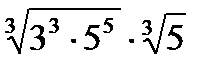
№ 4. Представить в виде степени:
1) 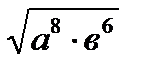 2)
2) 
Вариант 1
1.Постройте часть графика функции:
а) y=sin x на [-2π;0];
б)y=cos x на [  ;
;  + 2π];
+ 2π];
в) y=ctg x на (0;2π).
2.Пусть 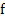 (x) = sin 2x + cos x.Найдите:
(x) = sin 2x + cos x.Найдите:
а) f(0);
б) f(  );
);
в) f(  ).
).
3.Среди чисел  , π,
, π,  ,
,  ,
, 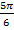 ,
,  укажите решения уравнения sin 3x-sin x – 0,5=0.
укажите решения уравнения sin 3x-sin x – 0,5=0.
4.Докажите, что при всех значениях х
-11 ≤ 4 cos x + 7 sin x ≤ 11.
5. Найдите наименьшее значение выражения
4 cos x + 7 sin x
Вариант 2
1. Пусть f(6) = -3, а f(-1,5) = 4. Найдите f(-6) и f(1,5), если:
а) f(x)-нечетная функция;
б) f(x)-четная функция;
в) f(x)-периодическая функция с периодом T=3.
2. Какое значение функция y=sin x принимает на [π;2π] ровно один раз?
3. Найдите область определения функции:
а) y= 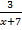 ;
;
б) 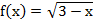 .
.
4. Найдите нули функции:
а) 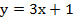 ;
;
б) 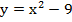 .
.
5.При каких значениях t функция y=2t-1 принимает отрицательные значения?
Тема 6
«Прямые и плоскости в пространстве»
1 вариант
1. Основание АD трапеции АВСD лежит в плоскости α. через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. Е и F не принадлежат АD.
а) Каково взаимное расположение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если угол АВС равен 150°? Ответ обоснуйте.
2. Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите. что полученный четырехугольник – ромб.
Дан треугольник АВС, Е  АВ, К
АВ, К  ВС, ВЕ:ВА=2:5.
ВС, ВЕ:ВА=2:5.
Через прямую АС проходит плоскость α, не совпадающая с плоскостью треугольника АВС.
а) Докажите, что ЕК  α. б) Найдите длину отрезка АС, если ЕК=4
α. б) Найдите длину отрезка АС, если ЕК=4
2 вариант
1. Треугольники АВС и АСD лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DC.
а) Каково взаимное расположение прямых РК и АВ?
б) Чему равен угол между прямыми РК и АВ, если угол АВС равен 40° и угол ВСА равен 80°? Ответ обоснуйте.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е  СD, К
СD, К  DА, DЕ:ЕС=1:2, DК:КА=1:2.
DА, DЕ:ЕС=1:2, DК:КА=1:2.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник MNEK – трапеция.
Дан треугольник АВС, М  АВ, К
АВ, К  ВС, ВМ:МА=3:4.
ВС, ВМ:МА=3:4.
Через прямую МК проходит плоскость α, параллельная прямой АС.
а) Докажите, что ВС:ВК=7:3.
б) Найдите длину отрезка МК, если АС=14см.
Тема 7
«Многогранники и круглые тела»
Вариант-1
№ 1. Начертить правильную четырехугольную усеченную пирамиду. Записать формулы площади поверхности и объема этой пирамиды. Указать высоту и апофему.
№ 2 Стороны оснований правильного прямоугольного параллелепипеда равны 6 см и 8 см. Площадь диагонального сечения 180 см 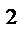 . Вычислить площадь боковой поверхности и объем параллелепипеда.
. Вычислить площадь боковой поверхности и объем параллелепипеда.
№ 3. Площадь осевого сечения конуса 36 см  . Высота конуса 12 см. Найти объем конуса и площадь боковой поверхности.
. Высота конуса 12 см. Найти объем конуса и площадь боковой поверхности.
Вариант-2
№1 Начертить усеченный конус. Записать формулы площади поверхности и объема этого конуса.
№2. В правильной четырехугольной пирамиде площадь полной поверхности пирамиды 384 см  , площадь боковой поверхности 240см
, площадь боковой поверхности 240см  . Найти длину стороны основания и апофему пирамиды.
. Найти длину стороны основания и апофему пирамиды.
№3 Площадь боковой поверхности конуса 108 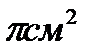 .Образующая конуса 12 см. Найти площадь полной поверхности конуса и объем.
.Образующая конуса 12 см. Найти площадь полной поверхности конуса и объем.
5 – «5»
4 – «4»
3 – «3»
2 – «2»
Тема 8
«Начала математического анализа»
1 вариант
А1. Найдите f `(4), если f ( x ) = 4 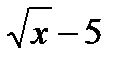 .
.
1) 3; 2)2; 3) -1; 4) 1.
А2. Укажите производную функции 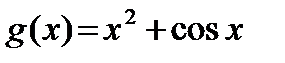 .
.
1)  ; 2)
; 2) 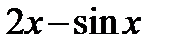 ; 3)
; 3)  ; 4)
; 4)  .
.
А3. Уравнение касательной к графику функции 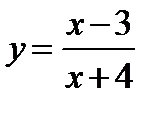 в точке с абсциссой х0 = -3 имеет вид:
в точке с абсциссой х0 = -3 имеет вид:
1) 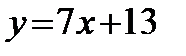 ; 2)
; 2) 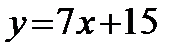 ; 3)
; 3)  ; 4)
; 4)  .
.
А4. Тело движется по прямой так, что расстояние S (в метрах) от него до точки B этой прямой
изменяется по закону 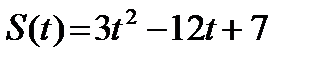 (t – время движения в секундах). Через сколько секунд
(t – время движения в секундах). Через сколько секунд
после начала движения мгновенная скорость тела будет равна 72 м/с.
1) 16; 2)15; 3) 14; 4) 13.
В5. На рисунке изображён график производной некоторой функции 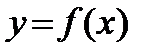 , заданной на
, заданной на
промежутке ( - 3; 3). Сколько точек максимума имеет функция  на этом промежутке?
на этом промежутке?

В6. Найдите угловой коэффициент касательной к графику функции  в точке
в точке 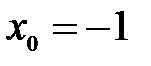 .
.
В7.Найдите производные функций: а) 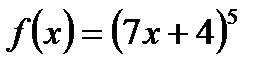 ; б)
; б)  .
.
С8. Найдите сумму тангенсов углов наклона касательных к параболе  в точках
в точках
пересечения параболы с осью абсцисс.
2 вариант
А1. Найдите f `(16), если f ( x ) = 8 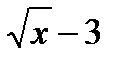 .
.
1) 3; 2)2; 3) -1; 4) 1.
А2. Укажите производную функции 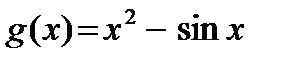 .
.
1) 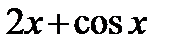 ; 2)
; 2) 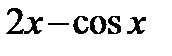 ; 3)
; 3)  ; 4)
; 4)  .
.
А3. Уравнение касательной к графику функции  в точке с абсциссой х0 = -3 имеет вид:
в точке с абсциссой х0 = -3 имеет вид:
1) 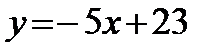 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 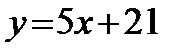 .
.
А4. Тело движется по прямой так, что расстояние от начальной точки изменяется по закону
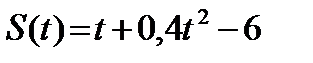 (м), где t – время движения в секундах. Найдите скорость тела через 10
(м), где t – время движения в секундах. Найдите скорость тела через 10
секунд после начала движения .
1) 10; 2)9; 3) 8; 4) 7.
В5. На рисунке изображён график производной некоторой функции 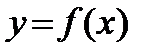 , заданной на
, заданной на
промежутке ( - 2; 2). Сколько точек минимума имеет функция  на этом промежутке?
на этом промежутке?
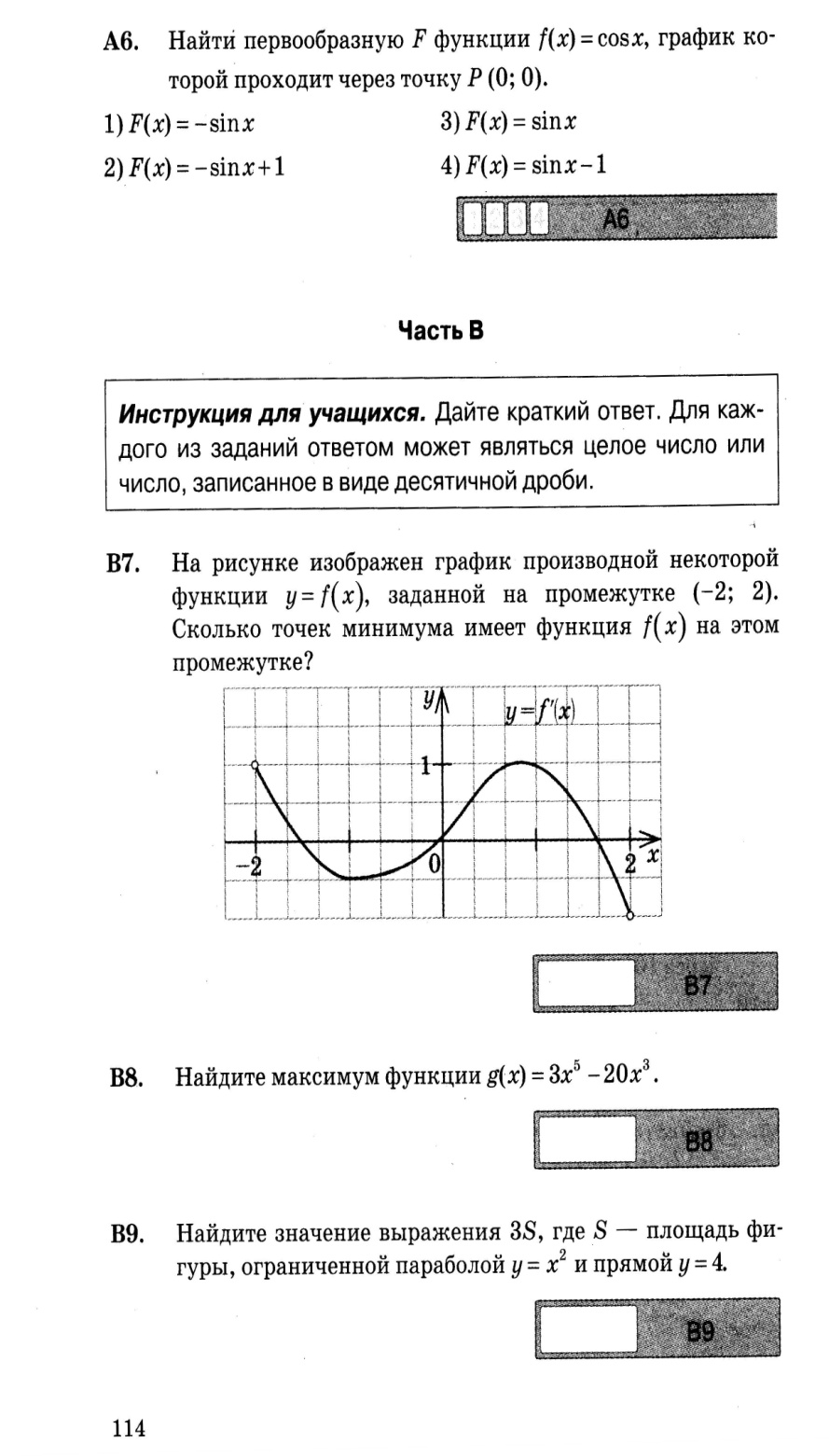
В6. Найдите угловой коэффициент касательной, проведенной к графику функции  в точке
в точке 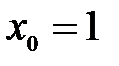 .
.
В7.Найдите производные функций : а) 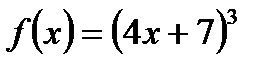 ; б)
; б)  .
.
С8. Найдите сумму угловых коэффициентов касательных к параболе 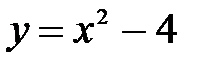 в точках
в точках
пересечения параболы с осью абсцисс.
Тема 9
«Интеграл и его применение»
1 вариант
А1. . Вычислите интеграл:
а) 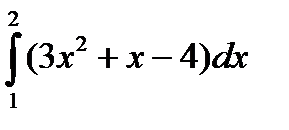 ; б)
; б)  .
.
А2. Для функции f ( x ) = 3sin x найдите:
а) множество всех первообразных;
б) первообразную, график которой проходит через точку М (  ; 0 )
; 0 )
А3. Вычислите, сделав предварительно рисунок, площадь фигуры, ограниченной линиями:
у = 0,5 х2, у = 0, х = 2, х = 0.
А4. Докажите, что функция F является первообразной для функции f ( x ) на промежутке
( - ∞ ; +∞), если F (х) = х3 – 4, f ( x ) = 3х2.
В5. Вычислите интеграл 
С6. Найдите площадь фигуры, ограниченной линиями у = 6х – х2 и у = 2х.
2 вариант
А1. . Вычислите интеграл:
а) 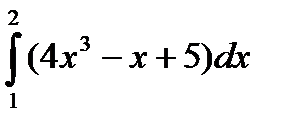 ; б)
; б) 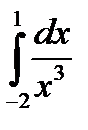 .
.
А2. Для функции f ( x ) = 2cos x найдите:
а) множество всех первообразных;
б) первообразную, график которой проходит через точку М ( 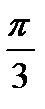 ; 0 )
; 0 )
А3. Вычислите, сделав предварительно рисунок, площадь фигуры, ограниченной линиями:
у = 2 х2, у = 0, х = 3, х = 0.
А4. Докажите, что функция F является первообразной для функции f ( x ) на промежутке
( - ∞ ; +∞), если F (х) = 2х – x2, f ( x ) = 2 - 2х.
В5. Вычислите интеграл 
С6. Найдите площадь фигуры, ограниченной линиями у = - 6х – х2 и у = - 2х.
Рейтинг- 15 баллов.
15- 12– «5»
11-9 – «4»
8-5 – «3»
4-0 – «2»
Вариант 1
1. Даны точки А (1;2;3), В (3;2;-1), С (5;8;-1), Д (-6;4;0).
а) найдите абсолютную величину векторов АВ и СД.
б) найдите координаты векторов АВ, ВС, СД, АД, АС,СВ
2. Даны векторы а{3;-4;-3}, b{-5;2;-4}. Найдите координаты вектора с=4а-2b
3. При каком значении n данные векторы перпендикулярны:
А(2;-1;3), b (1;3;n)
4. Даны векторы а{3;-1;1}, b{-5;1;0}. Выясните, какой угол (острый, прямой, тупой) между данными векторами.
Вариант 2
1. Даны точки А (1;-2;1), В (0;-2;4), С (3;-2;1), Д (-3;4;1).
а) найдите абсолютную величину векторов АВ и СД.
б) найдите координаты векторов АВ, ВС, СД, АД, АС,СВ
2. Даны векторы а{3;-4;-3}, b{-5;2;-4}. Найдите координаты вектора d=2а-b
3. При каком значении n данные векторы перпендикулярны:
А(n;-2;1), b (n;-n;1)
4. Даны векторы а{-2;1;3}, b{-1;0;5}. Выясните, какой угол (острый, прямой, тупой) между данными векторами.
6– «5»
5-4 – «4»
3 – «3»
2-0 – «2»
Тема 11- 12» Комбинаторика, статистика и теория вероятностей»
1 вариант
А1. Для каждого из описанных событий определите, каким оно является: невозможным, достоверным или случайным:
1) завтра будет хорошая погода;
2) в январе в городе пойдет снег;
3) в 12 часов в городе идет дождь, а через 24 часа будет светить солнце;
4) на день рождения вам подарят говорящего крокодила;
5) круглая отличница получит двойку;
6) камень, брошенный в воду утонет.
А2. Определите моду, среднее арифметическое и размах ряда: 5, 6, 11, 11, – 1.
А3. Какова вероятность того, что задуманное двузначное число делится на 3 или делится на 2? Определите вид события.
| а) сложение событий; | б) произведение событий. |
А4. Вычислите  .
.
А5. На стол бросают два игральных тетраэдра (серый и белый), на гранях каждого из которых точками обозначены числа от 1 до 4. Сколько различных пар чисел может появиться на гранях этих тетраэдров, соприкасающихся с поверхностью стола?
А6. Из 10 первых натуральных чисел случайно выбираются 2 числа. Вычислите вероятности
следующих событий: а) одно из выбранных чисел – двойка; б) оба числа нечетные.
В7. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?
В8. На каждой карточке написана одна из букв к, л, м, н, о, п. Четыре карточки наугад выкладывают одну за другой в ряд. Какова вероятность, что при выкладывании получится слово «клоп»?
С9. Найдите вероятность того, что случайным образом выбранное двузначное число при делении на 11 дает в остатке 10.
2 вариант
А1. Для каждого из описанных событий определите, КОС оно является: невозможным, достоверным или случайным:
1) вы выходите на улицу, а навстречу идет слон;
2) вас пригласят лететь на Луну;
3) черепаха научится говорить;
4) выпадет желтый снег;
5) вы не выиграете, участвуя в беспроигрышной лотерее;
6) после четверга будет пятница.
А2. Определите моду, среднее арифметическое и размах ряда:15, 4, 12, – 3, 15.
А3. Какова вероятность того, что первое из задуманных двузначных чисел делится на 2, а второе – делится на 5? Определите вид события.
| а) сложение событий; | б) произведение событий. |
А4. Вычислите 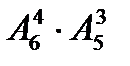 .
.
А5. Из коробки, содержащей 8 мелков различных цветов, Гена и Таня берут по одному мелку. Сколько существует различных вариантов такого выбора двух мелков?
А6. Из 10 первых натуральных чисел случайно выбираются 2 числа. Вычислите вероятности
следующих событий:
а) одно из выбранных чисел – единица; б) оба числа четные.
В7. В урне 6 белых и 4 черных шара. Из этой урны наудачу извлекли 5 шаров. Какова вероятность того, что 2 из них белые, а 3 черные?
В8. На каждой карточке написана одна из букв р, с, т, у, л, х. Четыре карточки наугад выкладывают одну за другой в ряд. Какова вероятность, что при выкладывании получится слово «стул»?
С9. Найдите вероятность того, что случайным образом выбранное двузначное число при делении на 13 дает в остатке 5.
15- 13– «5»
12-10 – «4»
9-5 – «3»
4-0 – «2»
УЧЕБНОЙ ДИСЦИПЛИНЫ
ОУД.04 . Математика
по программе подготовки специалистов среднего звена
по профессии среднего профессионального образования
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ МАТЕРИАЛЫ ДЛЯ ТЕКУЩЕГО КОНТРОЛЯ УСПЕВАЕМОСТИ ПО ДИСЦИПЛИНЕ ОУД.04 . Математика
Контрольные работы
Тема 1: «Развитие понятия о числе»
Вариант 1
1.Запишите число в стандартном виде:
а)730000000; б)0,0000025;
в)0,24 *10-3; г)75,2*104.
2. Представьте обыкновенную дробь в виде десятичной периодической дроби:
а) 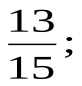 б)
б) 
3. Вычислите:
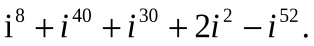
4. Найдите сопряжённое число комплексному числу:
z= 4 + 5i.
5. Обратите чистые периодические десятичные дроби в обыкновенные:
а) 0,(42); б) 0,(513).
6. Обратите смешанные периодические десятичные дроби в обыкновенные дроби:
а) 0,0(27); б) 0,0(01).
7. Даны числа z1= - 1 +3 i, z2= 4 + 5i. Вычислите:
а) модули чисел z1 и z2;
б) сумму чисел z1 и z2;
в) разность чисел z1 и z2;
г) произведение чисел z1 и z2.
8. Постройте комплексные числа в координатной плоскости:
z1= - 1 +3i, z2= 4 + 5i.
9. Найдите значение дроби:
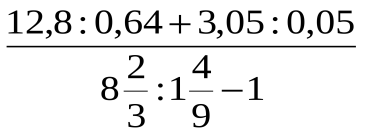
Дата: 2019-05-28, просмотров: 579.