| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 9
1. Вычислить:
а. 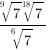 ; б.
; б.  ; в.
; в. 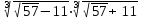 .
.
2. Найдите значение числового выражения:
а. 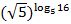 ; б.
; б.  ; в.
; в. 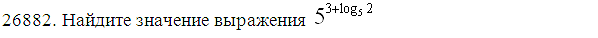 .
.
3. Сравните числа:
а. log4 0,3 и log7 2; б.  4 и
4 и 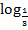 4.
4.
4. Упростите выражение:
а.  ; б.
; б. 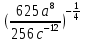 .
.
5. Сократить дробь:

6. Упростите выражение:
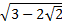
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 10
1. Вычислить:
а. 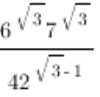 ; б.
; б.  ; в.
; в. 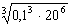 .
.
2. Найдите значение числового выражения:
а. log0,2 125 ; б . log9243 ; в . 
 .
.
3. Сравните числа:
а. 2  и 31log8 35 б. log5 7 и log3 6
и 31log8 35 б. log5 7 и log3 6
4. Упростите выражение:
а.  ; б.
; б. 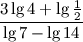 .
.
5. Сократить дробь:

6. Упростите выражение:
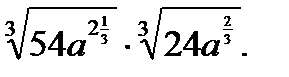
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 11
1. Вычислите:
а. ( 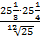 ) б.
) б.  в.
в. 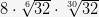
2. Найдите значение числового выражения:
а . log4 32; б . log2 4; в . log4 0,0626.
3. Сравните числа:
а. log20 4 и log80 8; б. 
4. Упростите выражение:
а. 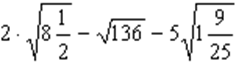 б.
б. 
5. Сократить дробь:
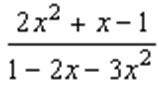
6. Упростите выражение:
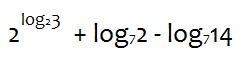
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 12
1. Вычислить:
а. 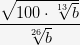 ; б.
; б.  ; в.
; в.  .
.
2. Найдите значение числового выражения:
а. 2 log3 2. б. 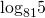 в.
в. 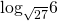
3. Сравните числа:
а. 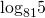 и
и 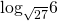 б.
б.  5 и -1
5 и -1
4. Упростите выражение:
а. 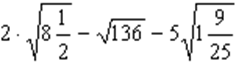 ; б.
; б. 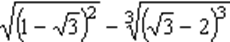 .
.
5. Сократить дробь:
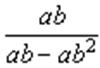
6. Упростите выражение:
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 13
1. Вычислить:
а. 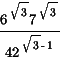 ; б.
; б. 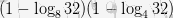 ; в.
; в. 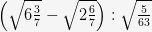 .
.
2. Найдите значение числового выражения:
а. log0,3 10; б . log 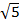 ; в. Log3 12.
; в. Log3 12.
3. Сравните числа:
а.  и
и 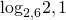 б.
б. 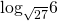 и
и 
4. Упростите выражение:
а. 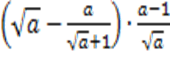 ; б.
; б. 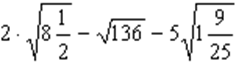 .
.
5. Сократить дробь:
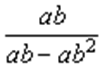
6. Упростите выражение:
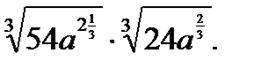
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 14
1. Вычислить:
а. 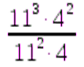 ; б.
; б. 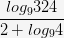 ; в.
; в. 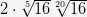 .
.
2. Найдите значение числового выражения:
а . log5 250 ; б . lg 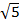 ; в log4 0,125.
; в log4 0,125.
3. Сравните числа:
а.  и
и 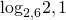 б.
б. 
4. Упростите выражение:
а.  ; б.
; б. 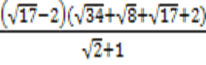 .
.
5. Сократить дробь:

6. Упростите выражение:
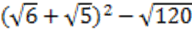
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 15
1. Вычислить:
а.  ; б.
; б. 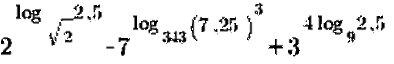 ; в.
; в. 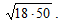
2. Найдите значение числового выражения:
а . log5 250 ; б . lg√5 ; в log4 0,125.
3. Сравните числа:
а. log4 26 и log6 17. б. 2 log3 и log 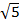
4. Упростите выражение:
а.  ; б.
; б. 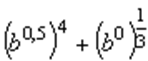 .
.
5. Сократить дробь:
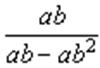
6. Упростите выражение:
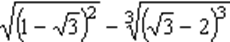
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант № 16 Вариант № 17
1) Основание прямоугольного параллелепипеда – квадрат. Сумма длин трёх рёбер, выходящих из одной вершины, равна 6 см. Какое наибольшее значение может иметь объём такого параллелепипеда?
1) Найдите высоту параллелепипеда наибольшего объёма, основание которого – прямоугольник периметра 3 см, а высота равна одной из сторон основания?
2) Исследовать функцию с помощью производной и построить график.
а) у = 6х2 – 2х3
б*) у = 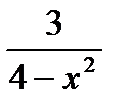
| а) у = 3/2х2 – х3
б*) у = 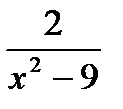
| в*) у = 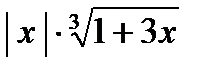 г*) у = г*) у = 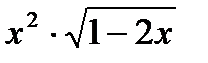 д*)
д*) 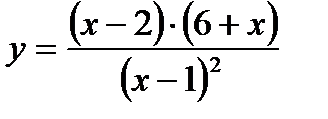 е*) е*) 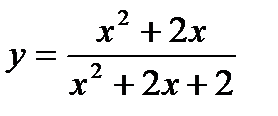
|
3) Найти наименьшее и наибольшее значения функции на промежутке.
а) f (х) = cos х – 1/3cos 3х на [0; п/2]
б*) у = х2 + 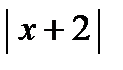 на [– 3; – 1]
в*) у = на [– 3; – 1]
в*) у = 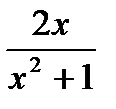 на ООФ на ООФ
| а) f (х) = sin х – 1/3sin 3х на [0; 3п/4]
б*) у =  на [– 1; 3]
в*) у = на [– 1; 3]
в*) у = 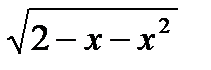 на ООФ на ООФ
|
Вариант № 18* Вариант № 19*
1) Графики – см. задание 2 из вариантов 1 и 2.
2) Найти наименьшее значение функции.
| f (x) = x + log2(2x + 2 – 5 + 2 – x + 2 ) | f (x) = x + log3(3x + 1 – 1 + 3 – x + 1 ) |
3) Найти наименьшее ( 2 в. – наибольшее ) значение выражения.
1 – (cos2 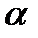 )1/2 – 2 sin2 )1/2 – 2 sin2 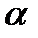
| 1 + (sin2 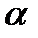 )1/2 + 2 cos2 )1/2 + 2 cos2 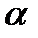
|
4) В фигуру, ограниченную параболой у = 4 – х2 и осью Ох, поместили прямоугольник, две вершины которого лежат на параболе, а две другие - на оси Ох. Найти наибольший из периметров этих прямоугольников.
5) Какую наибольшую площадь может иметь трапеция, три стороны которой равны р?
6) Фигура ограничена параболами у = х2 – 4х – 7 и у = – х2 + 9 . Найти наибольшую из длин отрезков, параллельных оси Оу и лежащих внутри данной фигуры.
7) Фигура ограничена параболой у = х2 и прямой у = 2х + 3 . Найти наибольшую из длин отрезков, параллельных оси Ох и лежащих внутри данной фигуры.
8) Из круга радиуса R вырезан сектор и из сектора склеен конус (боковая поверхность конуса). Каков наибольший объём получившейся конической воронки?
Дополнительные задания
9) Из всех прямоугольных треугольников, у которых сумма одного катета и гипотенузы равна р, найти треугольник с наибольшей площадью. Найти его площадь.
10) Найти МЗФ: 
11*) В какой точке графика функции у = (х – 1)2 , 0 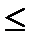 х
х 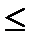 1, надо провести касательную к графику, чтобы площадь треугольника, ограниченного этой касательной и осями координат, была наибольшей?
1, надо провести касательную к графику, чтобы площадь треугольника, ограниченного этой касательной и осями координат, была наибольшей?
12*) На графике у = 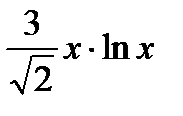 , где
, где 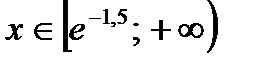 . Найти М (х; у), чтобы отрезок касательной к графику функции в этой точке, заключённый между точкой М и осью Оу, имел наименьшую длину.
. Найти М (х; у), чтобы отрезок касательной к графику функции в этой точке, заключённый между точкой М и осью Оу, имел наименьшую длину.
13*) Найдите кратчайшее расстояние от точки А до графика функции f (х), если А(1; 0), f (х) =  [А(– 3; 0), f (х) =
[А(– 3; 0), f (х) =  ].
].
14*) Исследовать функцию на выпуклость:
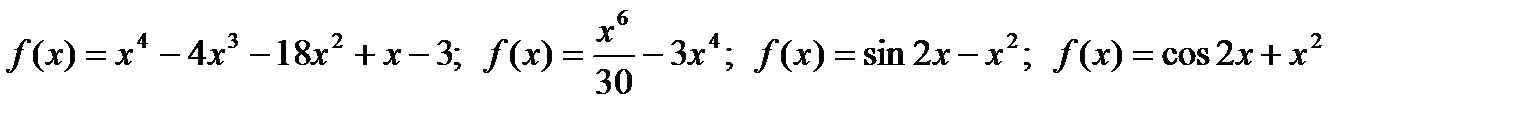
15*) Исследовать функцию с помощью производной и построить график.
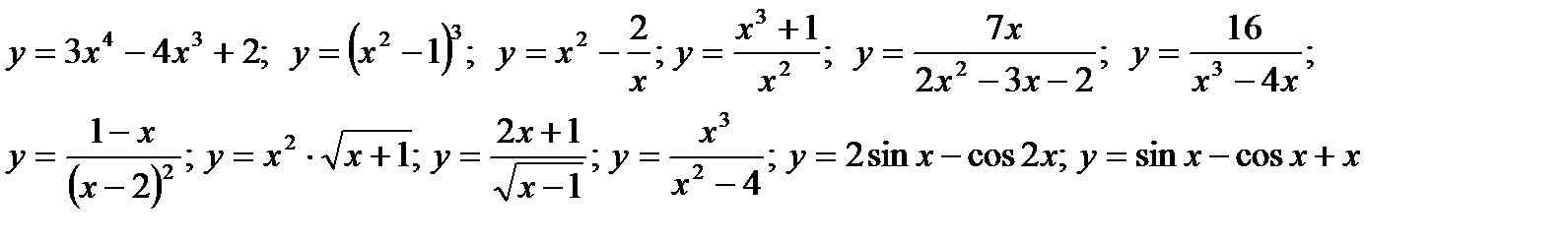
Дата: 2019-05-28, просмотров: 368.