| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 4 |
| « 4» (хорошо) | 3 |
| « 3» (удовлетворительно) | 2 |
| « 2 « (неудовлетворительно) | менее 1 |
Вариант 2
№1. Найдите значение выражения:
1) 
2) 
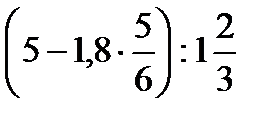3) 
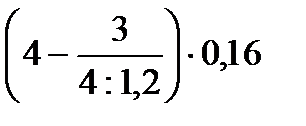
№ 2. Вычислить:
1) 
2) 
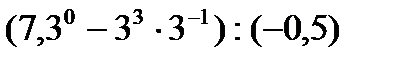
№ 3. Вычислить:
1) 
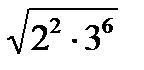
2) 
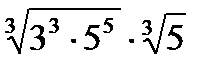
№ 4. Представить в виде степени:
1) 
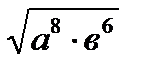2) 
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 5-6 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 3 |
Тема:5 «Функция, их свойства и графики»
Вариант 1
1.Постройте часть графика функции:
а) y=sin x на [-2π;0];
б)y=cos x на [ 
; + 2π];
в) y=ctg x на (0;2π).
2.Пусть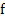 
(x) = sin 2x + cos x.Найдите:
а) f(0);
б) f( 
);
в) f( ).
3.Среди чисел , π, , 
, 
, 
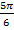укажите решения уравнения sin 3x-sin x – 0,5=0.
4.Докажите, что при всех значениях х
-11 ≤ 4 cos x + 7 sin x ≤ 11.
5. Найдите наименьшее значение выражения
4 cos x + 7 sin x
Вариант 2
1. Пусть f(6) = -3, а f(-1,5) = 4. Найдите f(-6) и f(1,5), если:
а) f(x)-нечетная функция;
б) f(x)-четная функция;
в) f(x)-периодическая функция с периодом T=3.
2. Какое значение функция y=sin x принимает на [π;2π] ровно один раз?
3. Найдите область определения функции:
а) y=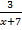 
;
б)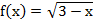 
.
4. Найдите нули функции:
а)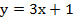 
;
б)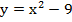 
.
5.При каких значениях t функция y=2t-1 принимает отрицательные значения?
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 4-5 |
| « 4» (хорошо) | 4 |
| « 3» (удовлетворительно) | 3 |
| « 2 « (неудовлетворительно) | менее 2 |
Тема 6
«Прямые и плоскости в пространстве»
1 вариант
1. Основание АD трапеции АВСD лежит в плоскости α. через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. Е и F не принадлежат АD.
а) Каково взаимное расположение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если угол АВС равен 150°? Ответ обоснуйте.
2. Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите. что полученный четырехугольник – ромб.
Дан треугольник АВС, Е 
АВ, К ВС, ВЕ:ВА=2:5.
Через прямую АС проходит плоскость α, не совпадающая с плоскостью треугольника АВС.
а) Докажите, что ЕК 
α. б) Найдите длину отрезка АС, если ЕК=4
2 вариант
1. Треугольники АВС и АСD лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DC.
а) Каково взаимное расположение прямых РК и АВ?
б) Чему равен угол между прямыми РК и АВ, если угол АВС равен 40° и угол ВСА равен 80°? Ответ обоснуйте.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е СD, К DА, DЕ:ЕС=1:2, DК:КА=1:2.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник MNEK – трапеция.
Дан треугольник АВС, М АВ, К ВС, ВМ:МА=3:4.
Через прямую МК проходит плоскость α, параллельная прямой АС.
а) Докажите, что ВС:ВК=7:3.
б) Найдите длину отрезка МК, если АС=14см.
Тема 7
«Многогранники и круглые тела»
Вариант-1
№ 1. Начертить правильную четырехугольную усеченную пирамиду. Записать формулы площади поверхности и объема этой пирамиды. Указать высоту и апофему.
№ 2 Стороны оснований правильного прямоугольного параллелепипеда равны 6 см и 8 см. Площадь диагонального сечения 180 см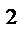 
. Вычислить площадь боковой поверхности и объем параллелепипеда.
№ 3. Площадь осевого сечения конуса 36 см 
. Высота конуса 12 см. Найти объем конуса и площадь боковой поверхности.
Вариант-2
№1 Начертить усеченный конус. Записать формулы площади поверхности и объема этого конуса.
№2. В правильной четырехугольной пирамиде площадь полной поверхности пирамиды 384 см 
, площадь боковой поверхности 240см 
. Найти длину стороны основания и апофему пирамиды.
№3 Площадь боковой поверхности конуса 108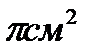 
.Образующая конуса 12 см. Найти площадь полной поверхности конуса и объем.
Дата: 2019-05-28, просмотров: 269.
