| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 9-8 |
| « 4» (хорошо) | 6-7 |
| « 3» (удовлетворительно) | 4-5 |
| « 2 « (неудовлетворительно) | менее 4 |
Вариант 2
1. Запишите число в стандартном виде:
а) 37000000; б)0,00000052;
в) 0,42*10-4; г)52,7*105.
2. Представьте обыкновенную дробь в виде десятичной периодической дроби:
а) 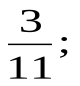 б)
б) 
3. Вычислите:

4. Найдите сопряжённое число комплексному числу:
z= 4 -7i.
5. Обратите чистые периодические десятичные дроби в обыкновенные:
а) 0,(72); б) 0,(918).
6. Обратите смешанные периодические десятичные дроби в обыкновенные дроби:
а) 0,3(6); б) 0,11(6).
7. Даны числа z1= - 3 +5i, z2= 4 -7i. Вычислите:
а) модули чисел z1 и z2 ;
б) сумму чисел z1 и z2;
в) разность чисел z1 и z2;
г) произведение чисел z1 и z2.
8. Постройте комплексные числа в координатной плоскости:
z1= - 3 + 5i, z2= 4 -7i.
9. Найдите значение дроби:
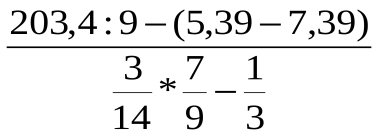
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 9-8 |
| « 4» (хорошо) | 6-7 |
| « 3» (удовлетворительно) | 4-5 |
| « 2 « (неудовлетворительно) | менее 4 |
Вариант 3
1) Найти производные функций.
а) 0,4х5 – 6 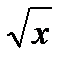 + 3ех
б) 2cos x + + 3ех
б) 2cos x + 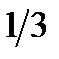 sin x – ln x + 5
в) sin x – ln x + 5
в) 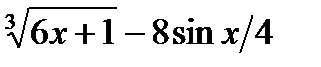 г)
г)  д)
д) 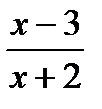
| а) 0,5х4 + 4/х – 3 ln x
б) 3sin x – 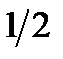 cos x + 2ех – 3
в) cos x + 2ех – 3
в) 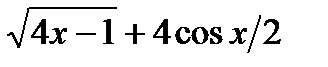 г)
г) 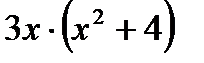 д)
д) 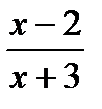
|
2) Решить уравнение f '(х) = 0, если
| а) f (х) = 1/2х + cos(х – п/3) б) f (х) = 2х3 – 3х2 + 1 | а) f (х) = – 1/2х + sin(х – п/6) б) f (х) = х3 + 1,5х2 – 1 |
3) Написать уравнение касательной к графику функции у = f (х) в точке с абсциссой хо, если
| f (х) = х2 + 2х, хо = – 2 | f (х) = х2 – 3х, хо = 3 |
4) Найти f '(х) и f '(0,25), если
f (х) = 
| f (х) = 
|
5) В какой точке графика функции у = 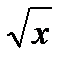 касательная наклонена к оси абсцисс под углом
касательная наклонена к оси абсцисс под углом 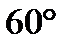 ( 2 в. :
( 2 в. :  )?
)?
6) Найдите острый угол, который образует с осью ординат касательная к графику функции у = f(x) в точке хо, если
f (х) = 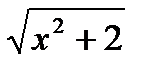 , хо = 1 , хо = 1
| f (х) =  , хо = 3 , хо = 3
|
Дополнительные задания 7) Найти производные функций.
а) cos23х
б) 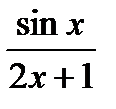 в)
в)  г) ln
г) ln 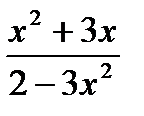 д) (sin х)1/2
е) ln(х2 + 3х)
д) (sin х)1/2
е) ln(х2 + 3х)
| а) sin2х/2
б)  в)
в) 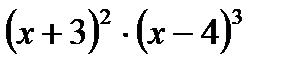 г) ln
г) ln 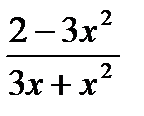 д) cos (1 + ех )
е) cos3х
д) cos (1 + ех )
е) cos3х
| а) 1/2 cos4(2x2 – 3)
б) 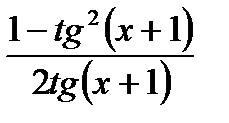 в) – 2 + x2sin x + 2x cos x
г)
в) – 2 + x2sin x + 2x cos x
г) 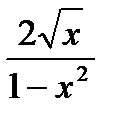 д) sin32x + cos32x
е)
д) sin32x + cos32x
е) 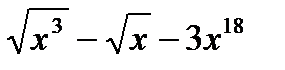
|
8) Написать уравнение касательной к графику функции
у =  , параллельной прямой у = 6х.
, параллельной прямой у = 6х.
9) Написать уравнение касательной к графику функции у = 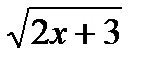 ,
,
проходящей через точку (– 2; 0).
10) Прямая касается гиперболы у = 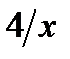 в точке (1; 4) . Найти площадь треугольника, ограниченного этой касательной и осями координат.
в точке (1; 4) . Найти площадь треугольника, ограниченного этой касательной и осями координат.
11*) Написать уравнение общих касательных к графикам функций
а) у = х2 + х и у = х2 – 3х; б) у = х2 и у = х3; в) у = 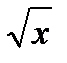 и у =
и у = 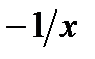 .
.
12*) Записать уравнение прямой, проходящей через точку (1/2; 2), касающейся графика у =  и пересекающей в двух точках график функции у =
и пересекающей в двух точках график функции у = 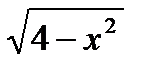 .
.
Вариант № 4* Вариант № 5*
1) Написать уравнение касательной к графику функции у = f (х) в точке
а) у = 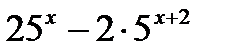 , в (.) еёминимума
б) у = , в (.) еёминимума
б) у = 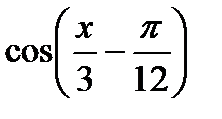 , в (.) с абсц. , в (.) с абсц. 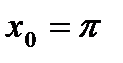
| а) у = 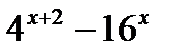 , в (.) её максимума
б) у = , в (.) её максимума
б) у = 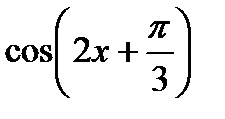 , в (.) с абсц. , в (.) с абсц. 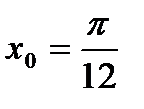
|
2) В каких точках касательная к гр-у функции у1 параллельна прямой у2?
у1 =  , у2 = , у2 = 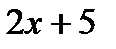
| у1 = 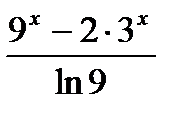 , у2 = , у2 = 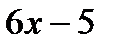
|
3) При каких значениях параметра р касательная, проведённая к графику функции в точке с абсциссой хо, проходит через точку М?
| у = х3 + 2рх, хо = 2, М (1; 2) | у = х3 + рх, хо = – 1, М (3; 2) |
4*) При каких значениях параметров прямые у1 и у2 касаются параболы?
| у1 = 5х – 6, у2 = – х, у = х2 + рх + с | у1 = 2х, у2 = 3х – 2, у = х2 + рх + с |
5) При каких значениях параметра р касательная к графику функции отсекает от 3 четверти ( 2 в. – от 1 четверти) равнобедренный треугольник, площадь которого равна 9/8 ( 2 в. = 25/8 )?
| у = 2р – х2 | у = – р – х2 |
6) При каких значениях параметров график функции у = х3 + рх2 + вх + с касается прямой у = 4х + 4 в точке с абсциссой х = – 1 и пересекает эту прямую в точке с абсциссой х = 2?
7) Хорда параболы у = х2 – 2х + 5 соединяет точки с абсциссами х1 = 1 и х2 = 3. Составить уравнения касательных параллельных хорде.
8) Прямая проходит через точки А(– 4; – 2) и В(0; 1) [ А(4; 6) и В(0; 1) ]. Определите, в какой точке она касается графика функции 
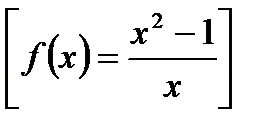 .
.
Дата: 2019-05-28, просмотров: 336.