Вариант 1
1. Найдите значение
а) sin 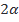 , если sin
, если sin 
б) cos ( 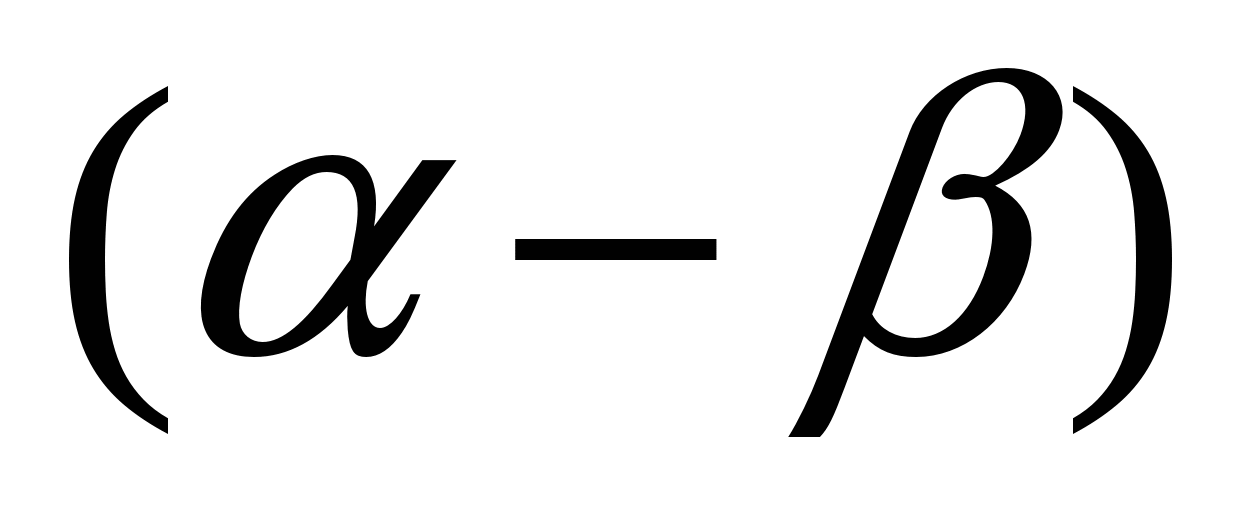 -2sin
-2sin 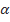 sin
sin  , если
, если 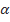 =30°; β=15°
=30°; β=15°
2. Упростите выражение:
а) cos2α+sin2α;
б) 1- 
3. Докажите, что sin40°+cos70°-cos10°=0
4. Представьте в виде произведения sinα- sin 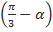
5. Найдите наибольшее и наименьшее значение выражения 5+ cos 
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 2-10 |
| « 4» (хорошо) | 9-7 |
| « 3» (удовлетворительно) | 6-4 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант 2
1. Найдите значение
а) cos 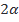 , если cos
, если cos 
б) cos 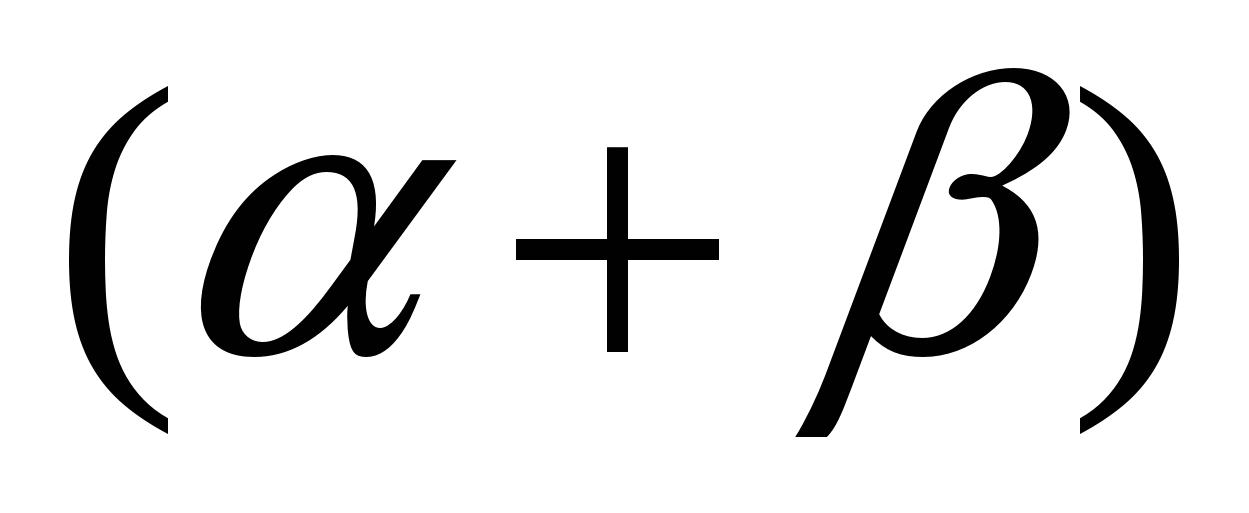 -2sin
-2sin  sin
sin  , если
, если  =75°; β=15°
=75°; β=15°
2. Упростите выражение:
а) cos2α+sin2α;
б) 1- 
3. Докажите, что сos12°+cos48°-sin18°=0
4. Представьте в виде произведения cosα-cos 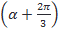
5. Найдите наибольшее и наименьшее значение выражения 5+ sin 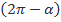
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 2-10 |
| « 4» (хорошо) | 9-7 |
| « 3» (удовлетворительно) | 6-4 |
| « 2 « (неудовлетворительно) | менее 3 |
Вариант № 3 Вариант № 4
1) Вычислить площадь фигуры, ограниченной линиями.

| 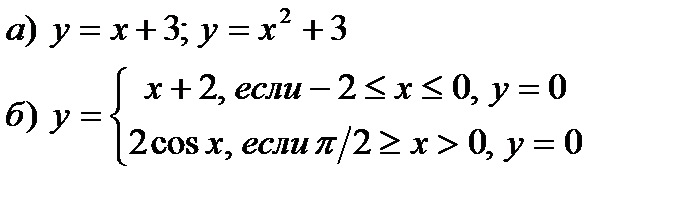
|
2) Вычислить интеграл.
а) 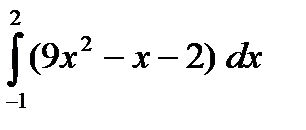 б)
б)  в)
в) 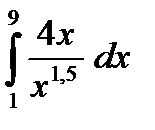 г)
г) 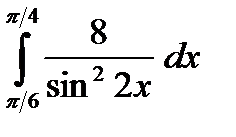 д)
д) 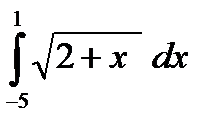
| а)  б)
б)  в)
в) 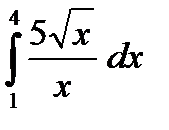 г)
г) 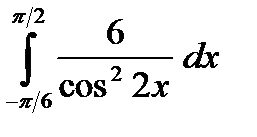 д)
д) 
|
3) Для функции f (x) найти первообразную, график которой проходит через точку М .
а) f (x) =  x2 – 3; M x2 – 3; M 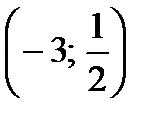 б) f (x) = cos
б) f (x) = cos 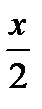 ; M ; M 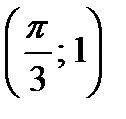
| а) f (x) = 2x2 – x; M 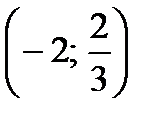 б) f (x) = sin 3x; M
б) f (x) = sin 3x; M 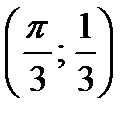
|
Дополнительные задания 4) Найти первообразные функции.
у =  ; у =
; у = 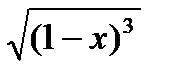 ; у = 2е – 3х + 1; у = 32х ; у = 2– 5х ; у =
; у = 2е – 3х + 1; у = 32х ; у = 2– 5х ; у = 
5) Вычислить интеграл
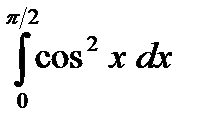 ;
; 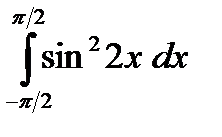 ;
; 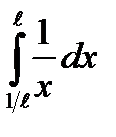 ;
;  ;
; 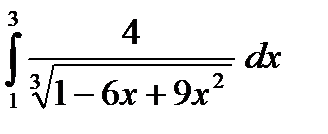 ;
; 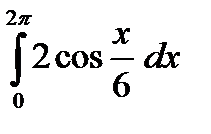 ;
;
 ;
;  ;
;  ;
;  ;
; 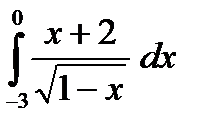 ;
; 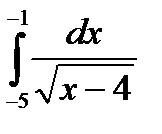
6) Вычислить площадь фигуры, ограниченной линиями,
а) f (x) = ех – 5, х = 0, х = 1 и Ох.
б) f (х) = – 2sin х, х = п, х =  п, у = 0.
п, у = 0.
в) f (х) = sin х/2, х = – п/3, х = п/3, у = 0.
г) f (х) = е 2х – 3, х = – 1, х = 1 и осью абсцисс.
д) f (х) = х2 – 4х + 5, касательной к графику в точке с абсциссой
хо = – 2 и осью ординат.
е) f (х) = sin х, касательной к графику в точке с абсциссой х0 = п и прямой х = п/2.
Вариант № 5* Вариант № 6*
1) Вычислить интеграл.
а) 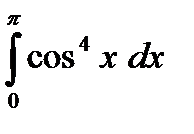 б)
б) 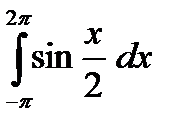 в)
в) 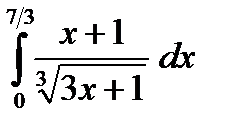 г)
г) 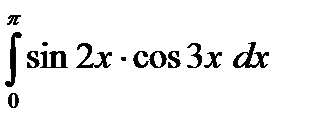 д)
д) 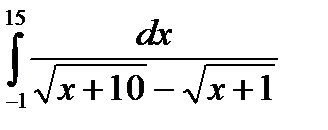 е)
е) 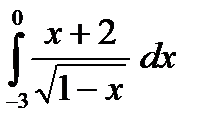 ж)
ж) 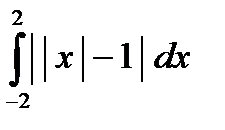 з)
з) 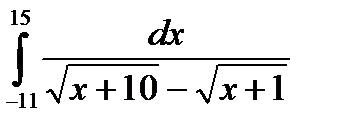
| а) 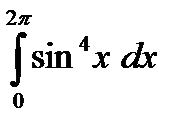 б)
б)  в)
в) 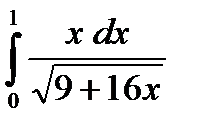 г)
г) 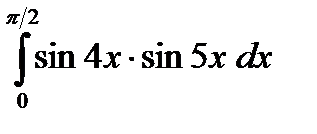 д)
д)  е)
е) 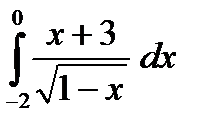 ж)
ж) 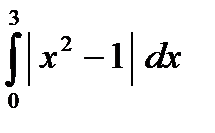 з)
з) 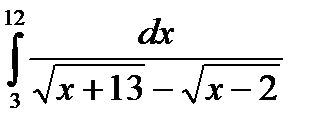
|
2) Найти максимумы ( 2 в. – минимумы ) функции
f (x) = 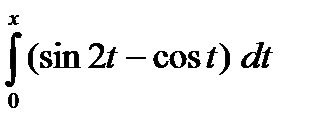 , 0 , 0 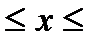 п п
| f (x) = 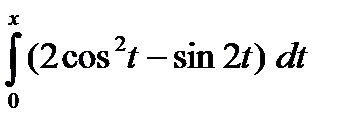 , 0 , 0 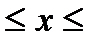 п п
|
3) Вычислить площадь фигуры, ограниченной линиями,
а) Осью Ох, у = 2х2 и касательной к этой кривой в точке с абсциссой равной 2.
б) у = х2 – 4х + 5 и прямыми, касающимися её в точках с абсциссами х1 = 2 и х2 = 4.
в) f (х) = сos х, касательной к графику в точке с абсциссой х0 = 5п/2 и прямой х = 2п.
г) у = 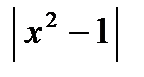 и у = 5 +
и у = 5 +  .
.
д) 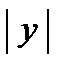 = 2х – х2.
= 2х – х2.
4) Какую часть площади квадрата отсекает парабола, проходящая через две соседние вершины квадрата и касающаяся середины одной из его сторон?
5*) Площадь фигуры, ограниченной линиями у = 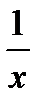 , у =
, у = 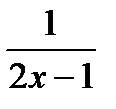 , х = 2,
, х = 2,
х = р, у = 0, равна ln  . Найдите р.
. Найдите р.
6) Найдите те первообразные функции f (x), графики которых
касаются прямой.
| f (x) = x2 – 5x + 3, y = – 3x – 1 | f (x) = x2 – x + 2, y = 2x – 1 |
7) Найти все значения параметра р, для каждого из которых выполняется неравенство.
а)  , р > 0
б) , р > 0
б) 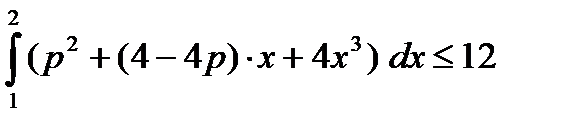
| а)  , р > 1
б) , р > 1
б) 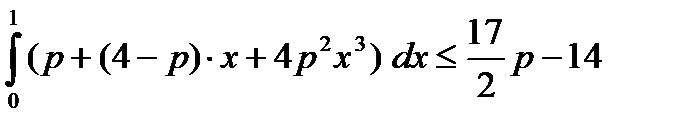
|
8) Найти а) наименьшее, б) наибольшее значение интеграла
а)  б)
б) 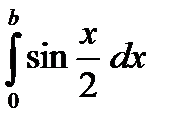
| а) 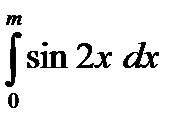 б)
б) 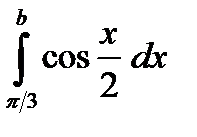
|
9) Для функции f (x) найдите первообразную, обладающую указанными свойствами а) f (x) = 4х + 8 [ f (x) = – х + 3 ] и график первообразной имеет только одну общую точку с прямой у = 3 [ у = 7 ];
б) график первообразной проходит через точки А(1; 10) и В(4; – 2), если  [ А(– 1; 4) и В(3; 4), если
[ А(– 1; 4) и В(3; 4), если 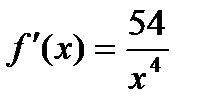 ].
].
Тема 4 «Уравнения и неравенства»
Вариант1.
1. Вычисление значений выражений.
№1. Найдите значение выражения:
1) 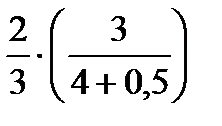 2)
2) 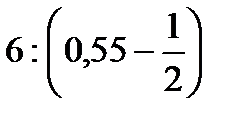 3)
3) 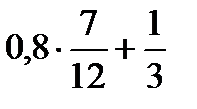 № 2. Вычислить:
№ 2. Вычислить:
1) 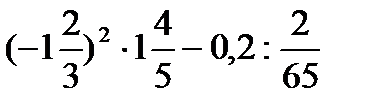
2) 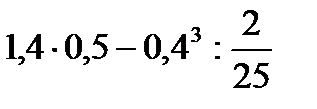
№ 3. Вычислить: 1) 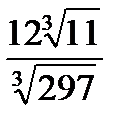 2)
2) 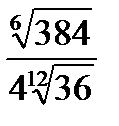
№ 4. Представить в виде степени:
1) 
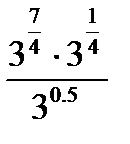 2)
2) 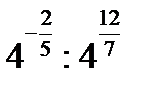
Дата: 2019-05-28, просмотров: 370.