Фактор времени учитывают с помощью методов наращения и дисконтирования.

Наращение - увеличение первоначальной суммы за счет начисленных процентов. Метод наращения позволяет определить будущую величину (future value – FV) современной стоимости (present value – PV) через некоторый промежуток времени n, исходя из заданной процентной ставки (или ставки роста) r ( interest rate).

Дисконтирование – способ определения современной стоимости (PV) по ее известному или предполагаемому значению в будущем (FV). Дисконтирование – операция, обратная наращению, с использованием процентной ставки (нормой дисконта) r.

В качестве процентной ставки r используют: стоимость заемных денежных средств; норму доходности производимых операций (отношение полученной прибыли к величине вложенных средств); альтернативную стоимость капитала.

Простые проценты.

Как правило, простые проценты используются в краткосрочных финансовых операциях, срок проведения которых меньше или равен году. Базой для исчисления процентов за каждый период в этом случае является первоначальная (исходная) сумма сделки. В общем случае наращение по годовой ставке простых процентов вычисляют по формуле:

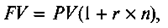
где FV— будущая стоимость (величина);

PV — современная величина;

n — число периодов (лет); 

r — процентная ставка.

На практике продолжительность краткосрочной операции обычно меньше года. В этом случае срок проведения операции корректируется следующим образом:

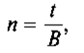
где t — число дней проведения операции;

В — временная база (число дней в году: 360, 365 или 366).

С учетом корректировки срока операции ее будущую стои­мость можно определить как:

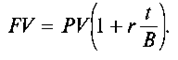
Обычно при определении продолжительности операции даты ее начала и окончания считаются за один день.

В процессе проведения анализа в качестве временной базы В удобно использовать условный, или финансовый, год, состоящий из 360 дней (12 месяцев по 30 дней). Исчисляемые по такой базе проценты называют обыкновенными, или коммерческими.

Точные проценты получают при базе, равной фактическому числу дней в году, т. е. при В = 365 или 366.

Дисконтирование по простым процентам

В зависимости от вида процентной ставки при анализе краткосрочных финансовых операций применяют два метода дисконтирования — математическое и коммерческое (так называемый банковский учет). В первом случае в качестве нормы приведения используют ставку г, применяемую при наращении. Во втором случае в роли нормы приведения выступает учетная ставка, для обозначения которой в дальнейшем будет использоваться символ d.

Математическое дисконтирование

Математическое дисконтирование представляет собой задачу, обратную наращению, и сводится к определению величины PV по известным значениям величин FV, r, n. С учетом принятых обозначений формула дисконтирования по ставке r будет иметь следующий вид:

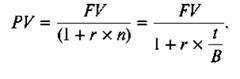
Разность FV- PV называют дисконтом, или скидкой, а используемую норму приведения r — декурсивной ставкой процентов.

В практике финансового управления более важную роль играют сложные проценты, которым в дальнейшем и будет уделено основное внимание.

Сложные проценты

Сложные проценты широко применяются в финансовых операциях, срок проведения которых превышает один год. Вместе с тем они могут использоваться и в краткосрочных финансовых операциях, если это предусмотрено условиями сделки либо вызвано объективной необходимостью (например, высоким уровнем инфляции, риска и т. д.). При этом база для исчисления процентов за период включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов.

Наращение по сложным процентам подразумевает реинвестирование полученных доходов. Процесс реинвестирования полученных доходов получил название капи­тализации. Общее соотношение для определения будущей величины имеет вид:

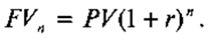
На практике, в зависимости от условий финансовой сделки, проценты могут начисляться несколько раз в году, например ежемесячно, ежеквартально и т. д. В этом случае соотношение для исчисления будущей стоимости будет иметь следующий вид:

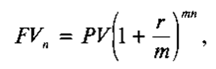 где m — число периодов начисления в году.

Дисконтирование по сложным процентам

Формулу для определения современной величины по сложным процентам можно легко вывести из формулы наращения делением её обеих частей на величину (1 + r)^n. Выполнив соответствующие ма­тематические преобразования, получим: