Волновые свойства микрочастиц

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

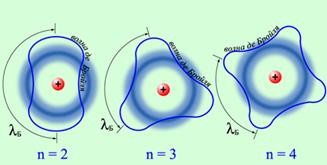
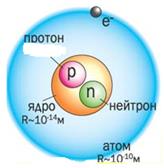
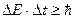Гипотеза де Бройля[53] основана на идее корпускулярно-волновой двойственности свойств частиц вещества.

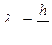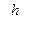Формула де Бройля устанавливает зависимость длины волны, связанной с движущейся частицей вещества, от импульса р частицы:

= ,

где т - масса частицы,

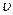- скорость частицы,

h = 6,625∙10^-34 Дж∙с – постоянная Планка.

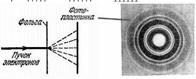
В 1948 году Л.М. Биберман, Н.Г. Сушкин и В. А. Фабрикант экспериментально подтвердили, что волновые свойства присущи не только потоку электронов, но и каждому электрону в отдельности.

Эксперимент показал, что даже в случае слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других, возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов, в миллионы раз более интенсивных.

Соотношения неопределенностей Гейзенберга[54]. Волновые свойства микрочастиц вносят ограничения в возможность применять к таким частицам понятия координаты и импульса в их классическом смысле.

Соотношениями неопределенностей Гейзенберга называются неравенства:

соотношение неопределенностей для координаты и импульса

соотношение неопределенностей для энергии и времени

Соотношение неопределенностей для координаты и импульса. Здесь

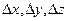означают интервалы координат, в которых может быть локализована частица, описываемая волной де Бройля, если проекции ее импульса по осям координат заключены в интервалах 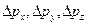соответственно. Соотношения Гейзенберга показывают, что координаты частицы х, у. z и проекции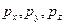 её импульса на соответствующие оси не могут одновременно иметь значения в точности равные х и р_х, у и р_y, z и р _z . Эти физические величины могут иметь значения, заданные с точностью, определяемой соотношениями Гейзенберга. Чем более точно определено положение частицы, т. е. чем меньше 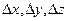, тем менее точно определены значения проекций ее импульса (т. е. тем больше 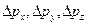). Если положение частицы на оси ОХ определено точно и 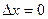, то 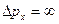и значение проекции импульса 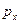становится совершенно неопределенным.

6.36.Найдите длину волны де Бройля для электрона, кинетическая
энергия которого равна 1 МэВ. [ 12,3 пм]

6.37.Найдите длину волны де Бройля для электронов, прошедших разность потенциалов: 1) 1 В, 2) 100 В. [1) 1,22∙10^{-9 м}; 2) 0,122∙10^-9 м]

6.38.Найдите длину волны де Бройля для атома водорода, движущегося при температуре 20 °С, с наиболее вероятной скоростью. [180пм]

6.39.Электронный пучок ускоряется в электроннолучевой трубке разностью потенциалов 1 кВ. Известно, что неопределенность скорости составляет 0,1 % от ее числового значения. Определите неопределенность координаты электрона. [61 нм]

6.40.Оцените неопределенность координаты электрона в электроннолучевой трубке, если составляющая импульса электрона определена с точностью 5∙10^-28 кг∙м/с.

6.41.Электрон с кинетической энергией 4 эВ локализован в области размером 1 мкм. Оцените с помощью соотношения неопределенностей относительную неопределенность его скорости.

6.42.Длительность возбужденного состояния атома водорода соответствует примерно 0,1 мкс. Какова неопределенность энергии в этом состоянии.

6.46.Принимая, что электрон находится внутри атома диаметром 0,3 нм, определите (в электрон-вольтах) неопределенность энергии этого электрона. [16,7 эВ]

Волновая функция и ее статистическая интерпретация. Положение частицы в пространстве в данный момент времени определяется в квантовой механике заданием волновой функции (пси-функции) .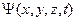

Вероятность 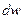того, что частица находится в элементе объема dV , пропорциональна 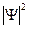и элементу объема dV :

= ,

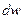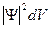где 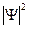- квадрат модуля 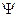-функции: 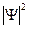= 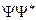. Здесь 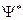- функция, комплексно сопряженная с 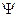-функцией.

Величина 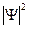есть плотность вероятности 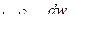- задает вероятность пребывания частицы в данной точке пространства. Интенсивность волны де Бройля определяется величиной .

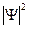Условие нормировки вероятностей следует из определения 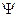-функции:

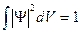где тройной интеграл по объему вычисляется по координатам, х, у и z от — 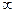до + 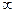, т. е. по всему бесконечному пространству.

Условие нормировки указывает на то, что пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице.

Уравнение Шрёдингера[55]. Временным уравнением Шрёдингера называется основное дифференциальное уравнение квантовой механики относительно волновой функции 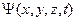. Оно определяет 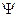-функцию для микрочастиц, движущихся в силовом поле с потенциальной энергией 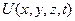со скоростью 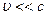, где с — скорость света в вакууме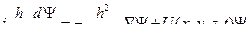

В уравнении: 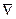- оператор Лапласа[56],

т - масса частицы,

h = 6,625∙10^-34 Дж∙с – постоянная Планка

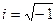- мнимая единица.

Уравнение Шрёдингера дополняется условиями, которые накладываются на 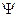-функцию:

а) функция должна быть конечной, однозначной и непрерывной;

б) производные 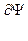, 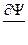и 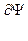должны быть непрерывны,

в) функция 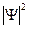должна быть интегрируема, т.е. интеграл должен быть конечным. Это условие в простейших случаях сводится к условию нормировки вероятностей.

Стационарное уравнение Шрёдингера 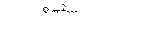- для случая, когда 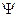-функция не зависит от времени ,

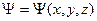В уравнении: E – полная энергия частицы.

Функции 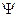, удовлетворяющие уравнению Шредингера при заданном виде потенциальной энергией 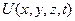, называются собственными функциями. Они существуют лишь при определенных значениях E, называемых собственными значениями энергии. Совокупность собственных значений E образует энергетический спектр частицы.

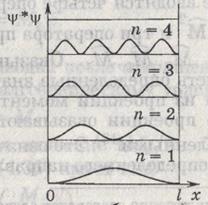
Стационарное уравнение Шрёдингера для частицы в потенциальной яме имеет вид:

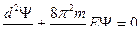или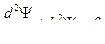

при краевых условиях 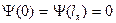, означающих, что 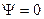и 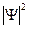=0 вне области 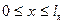, т. е. что вероятность найти частицу вне потенциальной ямы равна нулю.

Решение уравнения Шрёдингера:

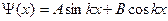
где А и В - постоянные,

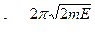- волновое число.

Вероятность обнаружить частицу в любой точке пространства постоянна.

Для волны, распространяющейся в положительном направлении оси ОХ,

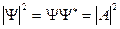, где А-нормировочный коэффициент.

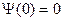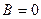Из краевых условий следует, что так как , то ; и 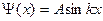, , 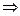, ,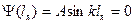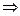решением уравнения 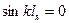является

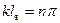, т.е. волновое число принимает ряд дискретных значений, соответствующих требованию:

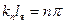, где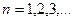

Последнее уравнение означает, что:

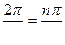или .

На длине потенциальной ямы должно укладываться целое число полуволн де Бройля.

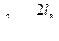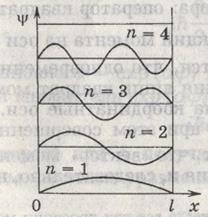
Из графиков, например, следует, что в состоянии с n=2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы несовместимо с представлениях о траекториях.

Собственные значения 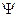функции уравнения Шрёдингера находятся из условия

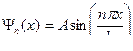Для нахождения коэффициента 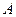воспользуемся условием нормировки согласно которому должно выполняться равенство 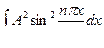=1

Произведем интегрирование[57]

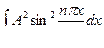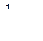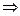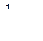= , , =1, 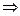, 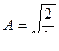. Таким образом, собственные функции имеют вид

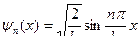Квантованными физическими величинами называются величины, которые могут принимать лишь определенные дискретные значения.

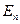Квантование энергии. Собственные значения энергии

частицы в одномерной потенциальной яме бесконечной глубины имеют дискретный характер

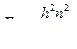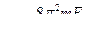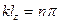Так как , а , то

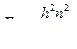Квантованные значения E_n называются уровнями энергии, а числа 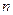, определяющие энергетические уровни частицы в потенциальной яме, называются квантовыми числами.

При больших квантовых числах происходит относительное сближение энергетических уровней частицы в потенциальной яме.

Туннельным эффектом называется прохождение («просачивание») частиц сквозь потенциальные барьеры.

Туннельный эффект является квантовомеханическим эффектом, связанным с тем, что частицы обладают волновыми свойствами.

Парадокс туннельного эффекта заключается в том, что прохождение частицы сквозь потенциальный барьер позволяет обнаружить ее в области запрещенной с классической точки зрения, где потенциальная энергия частицы превышает ее энергию.

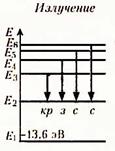
Квантовые характеристики электрона. Теория Бора приписывала четырем электронным оболочкам К, L, M и N квантовое число и, равное соответственно 1, 2, 3 и 4. Эти числа соответствуют повышающимся энергетическим уровням оболочек. Однако электронные оболочки в действительности расщеплены на подоболочки, каждая со своим собственным квантовым энергетическим уровнем.

n	1	2	3	4
Обозначение оболочки	K	L	M	N

l	0	1	2	3
Обозначение подоболочки	s «резкая» (sharp)	p «главная» (principal)	d «диффузная» (diffuse)	f «фундаментальная» (fundamental)

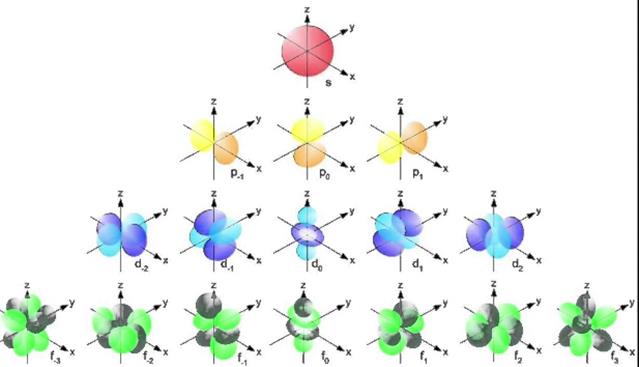
Линии, обусловленные переходами между этими подоболочками, испытывают дальнейшее расщепление, если атомы элементов помещены во внешнее магнитное поле. Это расщепление называется эффектом Зеемана. Экспериментально установлено, что указанное расщепление возможно только для р-, d- и f-подоболочек. Каждый энергетический уровень, на который они расщепляются в магнитном поле, соответствует одной орбитали в подоболочке. Магнитное поле не оказывает влияния на s-подоболочку, так как она состоит всего из одной s-орбитали сферической формы.

В отсутствие магнитного поля все орбитали одной подоболочки имеют одинаковую энергию. Орбитали, имеющие одинаковую энергию, называются вырожденными.

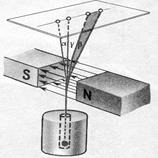
Атомные спектры элементов при определенных условиях обнаруживают расщепление, обусловленное наличием у электрона особого свойства -спина, которое можно представить себе как вращение электрона вокруг собственной оси. По направлению это вращение может быть правосторонним (по часовой стрелке) либо левосторонним (против часовой стрелки).

Таким образом, энергетический уровень электрона в атоме определяется следующими четырьмя характеристиками: оболочкой, подоболочкой, орбиталъю и спином. Каждой из этих характеристик сопоставляется определенное квантовое число.

Четыре квантовых числа характеризуют состояние каждого электрона в атоме:

Квантовые числа

Обозначение	Наименование	Принимаемые значения
n	главное	1,2,3…
l	орбитальное	0,1,2,…,(n-1)
m_l	магнитное	0,±1,±2,±… ±l
s m_s	спиновое магнитное спиновое	±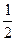

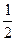
Следует отметить, что каждый электрон имеет свой индивидуальный набор квантовых чисел, которым он отличается от всех других электронов данного атома.

В 1925 г. Паули установил квантово - механический принцип (принцип запрета Паули): в любом атоме не может быть двух электронов, находящихся в одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел: n, l , m, ms.

Принцип Паули дал возможность теоретически обосновать периодическую систему элементов Менделеева, создать квантовые статистики, современную теорию твердых тел и др.

Для одного фиксированного значения главного квантового числа n существует 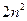различных квантовых состояний электрона.

Принцип Паули дает объяснение периодической повторяемости свойств атома, системе Менделеева.

Порядковый номер химического элемента Z равен общему числу электронов в атоме.

Если Z - число электронов в атоме, находящихся в состоянии, которое задается набором 4-х квантовых чисел n, l, m, m_s, то Z(n, l, m, m_s) = 0 или 1.

Если Z - число электронов в атоме, находящихся в состояниях, определяемых набором 3-х квантовых чисел n, l, m, то Z(n, l, m)=2. Такие электроны отличаются ориентацией спинов.

Если Z - число электронов в атоме, находящихся в состояниях, определяемых 2-мя квантовыми числами n, l,то Z(n, l)=2(2l+1).

Если Z - число электронов в атоме, которые находятся в состояниях, определяемых значением главного квантового числа n, то Z(n)= .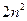

Электроны в атоме, занимающие совокупность состояний с одинаковыми значениями главного квантового числа n, образуют электронный слой: при n=1 К - слой; при n=2 L - слой; при n=3 М - слой; при n=4 N - слой; при n=5 О - слой и т.д.

6.47.Запишите возможные значения орбитального квантового числа l и магнитного квантового числа т _l для главного квантового числа п = 4.[ l =0, т _l = 0; l =1, т _l = 0, ±1; l =2, т _l = 0, ±1, ±2; l =3, т _l = 0, ±1, ±2, ±3]

6.48.Определите, сколько различных волновых функций соответствует главному квантовому числу п = 3.[9]

6.49.Постройте и объясните диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий (с учетом правил отбора) при переходах между состояниями с l = 2 и l = 1.

6.50.Определите числовое значение: 1) собственного механического момента импульса (спина); 2) проекции спина на направление внешнего магнитного поля.

6.51.Учитывая принцип Паули, определите максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом.

6.52.Заполненной электронной оболочке соответствует главное квантовое число п=3 . Определите число электронов на этой оболочке, которые имеют одинаковые квантовые числа: 1) m_s= -1/2 ; 2) m_l = 0; 3) m_l =-1, m_s =1/2.[1) 9; 2) 6; 3) 2]

6.53.Заполненной электронной оболочке соответствует главное квантовое число п = 4. Определите число электронов на этой оболочке, которые имеют одинаковые квантовые числа: 1) т _l=-3; 2) m_s =1/2, l=2;3) m_s=-l/2, т _l =1.[1) 2; 2) 5; 3) 3]

6.54.Запишите квантовые числа, определяющие внешний, или валентный, электрон в основном состоянии атома натрия.[n=3, l =0, т _l =0, m_s =±1/2]

Раздел 4. Физика ядра

Основные формулы

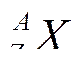
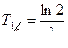
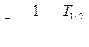
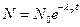
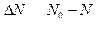
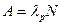
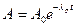
-зарядовое число -номер атома в таблице Д.И. Менделеева -число протонов в ядре

Правила смещения

a- распад	β^- - распад	β⁺ - распад

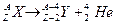
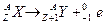
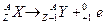
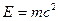
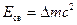
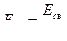
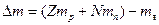
Энергия связи, приходящаяся на 1 а.е.м. (1 а.е.м.=1,660565∙10^{-27 кг), равна 931,4 МэВ.}

Энергия ядерной реакции: Q=c²[(m₁+m₂)-(m₃+m₄)]

Величина		Единица
Обозначение	Наименование	Единица
Z	порядковый номер водородоподобного элемента	-	-
N₀	число атомов в начальный момент времени
l _р	постоянная распада	1/с	1/с
τ	среднее время жизни атома радиоактивного вещества	с	с
А₀	начальная активность	Бк(беккерель)	с^-1
E _св	энергия связи	Дж	кг∙м²/c²
E _уд	удельная энергия связи	Дж/нуклон
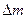
	дефект массы	кг	кг
m _р	масса протона	кг	кг
m_n	масса нейтрона	кг	кг
m _я	масса ядра	кг	кг

r₀ = 1,4∙10^{-15 м} – коэффициент пропорциональности

с ≈ 3∙10⁸ м/с – скорость света в вакууме

Масса частиц
электрона	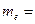9,1×10^–31кг » 5,5×10^–4 а.е.м.
протона	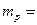1,672648586∙10^-27 кг=1,00727647011 а.е.м.
нейтрона	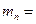1,674954386∙10^-27 кг=1,00866501237 а.е.м.

Масса нейтральных атомов

Элемент

Порядко-вый номер

Изотоп

Масса, а.е.м.

Элемент

Порядко-вый номер

Изотоп

Масса, а.е.м.

(Нейтрон)	0	п	1,00867	Азот	7	¹³ N	13,00574
Водород	1	¹Н	1,00783			¹⁴ N	14,0030
		²Н	2,01410			¹⁵ N	15,00011
		³Н	3,01605	Кислород	8	¹⁶ O	15,99491
Гелий	2	³Не	3,01603			¹⁷ О	16,99913
		⁴ Не	4,00260			¹⁸ O	17,99916
Литий	3	⁶ Li	6,01513	Фтор	9	¹⁹ F	18,99840
		⁷ Li	7,01601	Натрий	11	²² Na	21,99444
Бериллий	4	⁷ Be	7,01693			²³ Na	22,98977
		⁹ Be	9,01219	Магний	12	²³ Mg	22,99414
		¹⁰ Be	10,01354	Алюминий	13	³⁰ Al	29,99817
Бор	5	⁹B	9,01333	Кремний	14	³¹ Si -	30,97535
		¹⁰ В	10,01294	Фосфор	15	³¹ P	30,97376
		¹¹ В	11,00931	Калий	19	⁴¹ K	40,96184
Углерод	6	¹⁰ С	10,00168	Кальций	20	⁴⁴ Ca	43,95549
		¹² С	12,00000	Свинец	82	²⁰⁶ Pb	205,97446
		¹³ С	13,00335	Полоний	84	²¹⁰ Po	209,98297
		¹⁴ С	14,00324

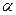Радиоактивность - превращение атомных ядер в другие ядра, сопровождающееся испусканием различных частиц и электромагнитного излучения. Отсюда и название явления: на латыни radio – излучаю, activus – действенный.

- излучение - ионизирующее излучение, состоящее из альфа-частиц (ядра атома гелия 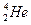), характеризующееся малой проникающей способностью (от него защищает ткань, лист бумаги) и высокой относительной биологической эффективностью; используется в лучевой терапии;

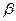-излучение (бета-лучи) - поток электронов ( 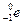) или позитронов ( 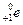), испускаемых при бета-радиоактивном распаде атомов, для защиты от него используются толстые слои металла;

γ -излучение – поток высокочастотного электромагнитного излучения, обладает высокой проникающей способностью, его можно ослабить, используя толстые листы свинца и железобетонные конструкции.

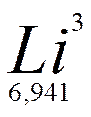
В ядерной физике участников ядерной реакции принято записывать:

Массовое число A может быть только целым, так как показывает количество нуклонов.

модель атома и ядра

Изотопы (от греч. isos — одинаковый и topos — место), разновидности атомов одного и того же химического элемента, атомные ядра которых содержат одинаковое число протонов и различное число нейтронов.

В ядрах водорода всегда 1 протон, а число нейтронов может быть равно 0 (протий), 1 (дейтерий), 2 (тритий).

Альфа-расп а д ( 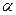-распад) – это испускание альфа-частиц атомными ядрами в процессе самопроизвольного (спонтанного) радиоактивного распада.

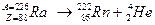
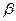Бета-распад ( -распад) - это радиоактивный распад атомного ядра, сопровождающийся вылетом из ядра электрона.

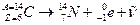
Этот процесс обусловлен самопроизвольным превращением одного из нуклонов ядра в нуклон другого рода, а именно превращением нейтрона ( 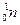) в протон ( ).

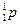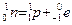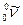
Период полураспада – это время, в течение которого распадается половина атомов данного количества радиоактивного вещества. Период полураспада обозначается Т.
Единицы измерения [c].

Ядерные силы - это силы взаимодействия между нуклонами; обеспечивают большую величину энергии связи. Ядерные силы являются наиболее важным и распространённым примером сильного взаимодействия. Ядерные силы примерно в 100 раз превосходят электростатические силы и на десятки порядков превосходят силы гравитационного взаимодействия нуклонов.

Ядерные силы не зависят от наличия или отсутствия у частиц электрического заряда, протоны и нейтроны ведут себя одинаково.

Особенностью ядерных сил является то, что они действуют на малых расстояниях, около 10^{-14 м.}

Энергия связи атомных ядер. Энергия связи ядра равна минимальной энергии, которую необходимо затратить для полного расщепления ядра на отдельные частицы. Из закона сохранения энергии следует, что энергия связи равна той энергии, которая выделяется при образовании ядра из отдельных частиц.

Е_св= ∆Мс²

c ≈ 3×10⁸ м/с– скорость света в вакууме;

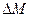- дефект массы, [кг] или [а.е.м.] (атомная единица массы[58])

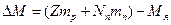
Z - зарядовое число;

m_p – масса протона, [кг] или [а.е.м.];

N_n - количество нейтронов;

m_n – масса нейтрона, [кг] или [а.е.м.];

M_я- масса ядра, [кг] или [а.е.м.];

N_р - количество протонов.

Ядерная реакция – это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением вторичных частиц или γ-квантов.

При ядерных реакциях выполняются законы сохранения: импульса, энергии, зарядового и массового числа.

6.55.Укажите второй продукт ядерной реакции: ²⁷₁₃Al + ¹₀n = ? + ⁴₂He.

6.56.Укажите второй продукт ядерной реакции: ¹⁴₇N + ⁴₂He = ¹₁H + ?

6.57.Какая доля радиоактивных атомов распадается через промежуток времени, равный двум периодам полураспада?

6.58.Определите период полураспада радиоактивного изотопа, если 5/8 начального количества ядер этого изотопа распалось за 849 с. [10 мин]

6.59.Постоянная радиоактивного распада изотопа 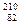РЬ равна 10^-9 с^-1. Определите время, в течение которого распадется 2/5 начального количества ядер этого радиоактивного изотопа. [16,2 лет]

6.60.Вычислите дефект массы и энергию связи ядра 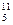В.[0,079 а.е.м.;73,64 МэВ]

6.61.Определите удельную энергию связи ядра 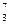Li .

6.62.Объясните, как изменится положение химического элемента в таблице Менделеева после a- и β-распадов ядер его атомов.

6.63. Ядро изотопа урана 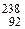U после нескольких радиоактивных распадов превратилось в ядро изотопа 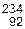U. Какие это были распады?

6.64.Пользуясь таблицей Менделеева и правилами смещения, определите, в какой элемент превращается 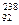U после трех a- и двух β -распадов.

6.65.Радиоактивный изотоп радия 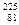Ra претерпевает четыре a -распада и два β - распада. Определите для конечного ядра: 1) зарядовое число Z; 2) массовое число А.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Детлаф А.А.,.Яворский Б.М. Курс физики. М.: Высшая школа, 1989.

2. Савельев И.В. Курс общей физики. М.: Наука, т. 1-3, 1978.

3. Яворский Б.М., Детлаф А.А. Справочник по физике. – М.: Наука, 1985.

4. Анисимов В.М., Данилова И.Н., Солохина Г.Э., Пронина В.С. Лабораторные работы по физике. Часть 1. Часть 2 / Под ред. Г.Г.Спирина, - М.: ОАО Авиаиздат, 2007.

5. Анисимов В.М., Третьякова О.Н.. Механика. Практический курс/ Под ред. Г.Г.Спирина, М.: ОАО Авиаиздат, 2007.

6. Анисимов В.М., Третьякова. Основы квантовой физики. Практический курс. / Под ред. . Г.Г.Спирина, М.: ОАО Авиаиздат, 2007.

7.Ваулин Е.Л., Гордеев О.А., Коновалова З.И.,.Мартыненко Т.П, Одинцова Г.А., Тарасов В.Е., Третьякова О.Н. Квантовая физика. Практический курс. /Под ред. проф. Г.Г.Спирина, - М.: ОАО Авиаиздат, 2007.

8.Лаушкина Л.А, Солохина Г.Э., Черкасова М.В. Молекулярная физика и термодинамика. Практический курс/Под ред. проф. Г.Г.Спирина, - М.: ОАО Авиаиздат, 2007.

9.Лаушкина Л.А., Солохина Г.Э., Хохлачева Г.М, Электромагнетизм. Практический курс /Под ред. проф. Г.Г.Спирина, - М.: ОАО Авиаиздат, 2007.

10.Рудакова Л.И., Соколова Е.Ю., Ющенко Т.А. Волновая оптика. Практический курс. /Под ред. проф. Г.Г.Спирина, - М.: ОАО Авиаиздат, 2007.

11.Яворский Б.М., Детлаф А.А. Справочник по физике. – М.: Наука, 1985.

СПРАВОЧНЫЙ ОТДЕЛ

Таблица 1.

Справочные данные

Постоянные величины	Приставки
G = 6,67×10^–11 Н∙м²/кг² N_А= 6,02×10²³моль^-1 k = 1,38×10^-23 Дж/К R = 8,31 Дж/(моль∙ К) к = 9×10⁹ Н∙м²/Кл² e₀= 8,85×10^-12 Ф/м c ≈ 3×10⁸ м/с h = 6,63×10^-34Дж∙с	Э экса 10¹⁸ П пэта 10¹⁵ Т тера 10¹² Г гига 10⁹ М мега 10⁶ к кило 10³ г гекто 10² да дека 10¹	д деци 10^-1 с санти 10^-2 м милли 10^-3 мк микро 10^-6 н нано 10^-9 п пико 10^-12 ф фемто 10^-15 аа а атто 10^-18

Таблица 2.

Диэлектрическая проницаемость некоторых веществ

Вещество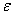
Вода (чистая)	81
Воздух	1,0006
Кварц	4,5
Парафин	2,3
Слюда	6-8
Стекло	4-7

Дата: 2019-04-23, просмотров: 402.

⇐ Предыдущая 17 18 19 20 21 22 23 242526 Следующая ⇒