Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Основные формулы

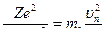
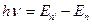
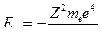
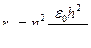     v =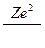   

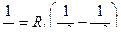
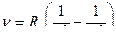  , n = 1, 2, 3, …; n΄ = n+1, n+2,…

Серия Лаймана (ультрафиолетовый диапазон)	Серия Бальмера (видимый диапазон)	Серия Пашена (инфракрасный диапазон)
n=1	n=2	n=3

 

            

                        

 

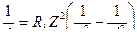
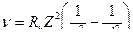
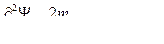
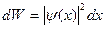
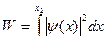
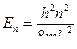
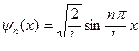
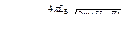
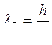
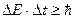
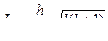
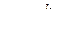
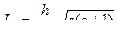
Квантовые числа

Обозначение	Наименование	Принимаемые значения
n	главное	1,2,3…
l	орбитальное	0,1,2,…,(n-1)
ml	магнитное	0,±1,±2,±… ±l
s   ms	спиновое   магнитное спиновое	±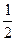

 

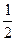
n	1	2	3	4
Обозначение оболочки	K	L	M	N

 

l	0	1	2	3
Обозначение подоболочки	s	p	d	f

 

Величина		Единица
Обозначение	Наименование
Z	порядковый номер водородоподобного элемента	-	-
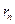
	радиус n-ой орбиты	м	м
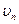
	скорость электрона на n-ой орбите	м/с	м/с
n	номер орбиты, главное квантовое число	-	-
ν	частота	Гц	1/с
λ	длина волны	м	м
Е	энергия	Дж	кг∙м2/с2
U	разность потенциалов, приложенная к рентгеновской трубке	В	кг∙м2/(А∙с3)
λБ	длина волны де Бройля	м	м
р	импульс частицы	кг∙м/c	кг∙м/c
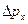
	неопределенность проекции импульса на ось х	кг∙м/c	кг∙м/c
Δх	неопределенность координаты	м	м
ΔЕ	неопределенность энергии данного квантового состояния	Дж	кг∙м2/с2
Δ t	время пребывания системы в данном квантовом состоянии	с	с
ψ(х)	волновая функция
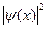
	плотность вероятности
dW	вероятность обнаружить частицу в интервале от x до х+dx
W	вероятность обнаружить частицу в интервале от x1 до х2
l я	ширина потенциального ящика	м	м
D	прозрачность потенциального барьера	-	-
U	высота потенциального барьера	Дж	кг∙м2/с2
m	масса	кг	кг
L	орбитальный момент импульса электрона	кг∙м/c	кг∙м/c
l	орбитальное квантовое число	-	-
LZ	проекция орбитального момента импульса электрона	кг∙м/c	кг∙м/c
L Б	ширина барьера	м	м
ml	магнитное квантовое число	-	-
ms	спиновое квантовое число	-	-
Т	абсолютная температура	К	К
n	концентрация	м-3	м-3
с V	молярная теплоемкость	Дж/(моль∙К)	кг∙м2/(мольК∙с2)

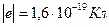
m_е = 9,1∙10^{-31 кг} – масса покоя электрона

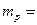1,672648586∙10^{-27 кг} – масса покоя протона

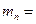1,674954386∙10^{-27 кг – масса покоя нейтрона}

e₀ = 8,85×10^-12 Ф/м – электрическая постоянная (диэлектрическая проницаемость вакуума)

R_λ=1,097∙10⁷ м^-1 – постоянная Ридберга  R_ν=R_l∙c=3,29∙10¹⁵ с^-1

h = 6,625∙10^-34 Дж∙с – постоянная Планка

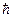=h/2π = 1,0545887∙10^-34 Дж∙с – редуцированная постоянная Планка или постоянная Дирака

с ≈ 3∙10⁸ м/с – скорость света в вакууме

k=1,38∙10^-23 Дж/К – постоянная Больцмана

Модели строения атома

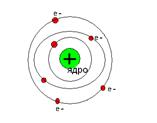
Модель Томсона[41] (пудинг с изюмом) 1903 г	Модель Резерфорда[42] (планетарная модель) 1911 г .	Модель Д.Д.Иваненко[43] и В.Гейзенберга[44] (протонно-нейтронная модель строения ядра) 1932 г .

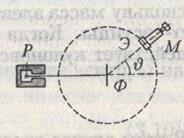
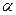Планетарная модель атома и опыты Резерфорда. Распределение положительных и отрицательных заря­дов в атоме можно выяснить, наблюдая изменение направления полета (рассеяние) -частиц при прохождении через тонкие слои вещества.

Опыт осуществлялся следующим образом. Выделяемый отверстием узкий пучок альфа-частиц, испускаемых радиоак­тивным веществом Р. падал на тонкую металлическую фольгу Ф. При прохождении через фольгу 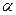-частицы от­клонялись от первоначального направления движения на различные углы - .

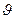Рассеянные 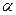-частицы ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции наблюдались в микроскоп M. Ми­кроскоп и экран можно было вращать вокруг оси, проходя­щей через центр рассеивающей фольги, и устанавливать таким образом под любым углом. Весь прибор поме­щался в откачанный кожух, чтобы устранить рассеяние 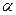-частиц за счет столкновений с молекулами воздуха.

Оказалось, что некоторое количество 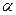-частиц рассеи­вается на очень большие углы (почти до 180°). Проанали­зировав результаты опыта, Резерфорд пришел к выводу, что столь сильное отклонение 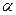-частиц возможно только в том случае, если внутри атома имеется чрезвычайно сильное электрическое поле, которое создается зарядом, связанным с большой массой и сконцентрированным в очень малом объеме. Основываясь на этом выводе, Ре­зерфорд предложил в 1911 г. ядерную модель атома.

Со­гласно Резерфорду атом представляет собой систему заря­дов, в центре которой расположено тяжелое положительное ядро с зарядом Ze, имеющее размеры, не превышающие 10^{-12 см, а вокруг ядра расположены} Z электронов, рас­пределенных по всему объему, занимаемому атомом. По­чти вся масса атома сосредоточена в ядре.

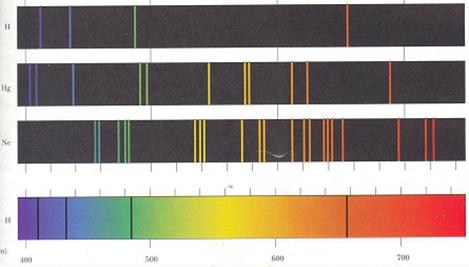
Энергетический спектр атомов и молекул - упорядоченная по длинам (частотам[45]) совокупность монохроматических волн, на которую разлагается свет или иное электромагнитное излучение. Типичный пример светового спектра - хорошо известная всем радуга.

Спектральным анализом называют совокупность физических методов качественного и количественного определения состава веществ в результате исследования их спектров излучения или поглощения.

Спектральный анализ является мощным средством исследования свойств веществ и установле­ния новых закономерностей микромира.

Спектр можно получить, разложив данное излучение с помощью спектрального прибора (дифракционной решетки, призмы и т.д.).

Оптический спектр – это спектр излучения[46] или спектр поглощения[47] оптического излучения.

Спектры излучения : совокупность частот (или длин волн), которые содержатся в излучении какого-либо вещества.

 

 

Спектры поглощения - это совокупность частот, поглощаемых данным веществом.

Спектры поглощения получают, пропуская свет от источника, дающего сплошной спектр, через вещество, атомы которого на­ходятся в невозбужденном состоянии.

 

Виды спектров	Состав спектра	Источники
Непрерывный	Содержит все длины волн определенного диапазона от красного с λ ≈ 7,6.10-7 м до фиолетового с λ ≈ 4.10-7 м	Излучают нагретые твердые и жидкие вещества, газы, нагретые под большим давлением
Линейчатый	Состоит из отдельных линий разного цвета (длины волны, частоты), имеющих разные расположения	Испускается газами в атомарном состоянии. Каждый атом излучает набор электромагнитных волн определенных частот. Каждый химический элемент имеет свой спектр
Полосатый	Состоят из широких спектральных полос, положение которых характерно для данного вещества	Испускается газом в молекулярном состоянии.

 

Характерным свойством всех атомов и молекул является то, что спектр каждого элемента, молекулы данного вещества индивидуален, неповторим и служит в спектральном анализе средством его идентификации ("удостоверением личности").

В настоящее время составлены каталоги спектров всех эле­ментов. Это позволяет выполнять поэлементный спектральный анализ сложных веществ путем расшифровки спектров в резуль­тате сравнения их с теми, которые находятся в каталогах спектров.

Спектр атома водорода.. Теоретический расчет спектров многоэлектронных атомов и молекул является очень сложной квантовомеханической (и мате­матической) задачей. Наиболее простыми системами, дающими линейчатые спектры, являются атом водорода и водородоподобные атомы или ионы, то есть такие, у которых на последней (валентной) электронной оболочке находится один электрон.

В 1885 г. швейцарский ученый Иоган Бальмер обратил внимание на закономерности расположения спектральных линий в видимой и близкой к ультрафиолетовой области спектра атома водорода.

 

Частоты (длины волн) спектральных линий для атома водорода и водородоподобных атомов, лежащих в видимой части спектра, определяются по формулам:

ν = R_ν ( 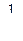 - 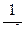), или = R_λ (  - ),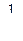

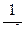где 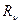 = 3,29∙10¹⁵ с^-1 или R_λ = 1,097∙10⁷ м^-1 – постоянные Ридберга.

В 1906 г. Теодор Лайман открыл спектральную серию в ультрафиолетовой части спектра водорода (серия Лаймана). Причем частоты спектральных линий для атома водорода и водородоподобных атомов могут быть определены по формулам:

ν = R_ν (1 - 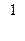) или = R_λ (1 - ),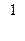

Фридрих Пашен обнаружил в 1908 г. первые две линии инфракрасного участка спектра, которые могут быть рассчитаны по формуле:

ν = R_ν (  - 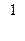) или = R_λ (  - ).

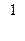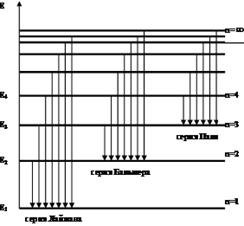
Все представленные серии спектральных линий атома водорода можно представить общими формулами:

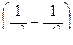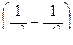ν = R_ν  или = R_λ . (1)

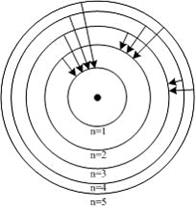
При n = 1 получается серия Лаймана, лежащая в далёкой ультрафио-летовой области спектра;

при n = 2 - серия Бальмера, линии которой расположены в видимой и близкой ультрафиолетовой областях;

При n = 3 - серия Пашена в инфракрасной области спектра.

Позже были обнаружены в инфракрасном диапазоне еще серии спектрального излучения, законы распределения которых также определяются формулами (1). Целые числа n и n₁ называются главными квантовыми числами, причем 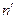 = n+1, n+2 и т.д.

Постулаты Бора . С точки зрения классической физики наличие спектральных линий у атомов объяснить невозможно. Согласно теории электромагнитного излучения движущаяся заряженная частица – электрон является источником электромагнитного излучения, в процессе движения и излучения электрон должен терять свою энергию постепенно, следовательно, атом должен излучать непрерывный спектр.

Датский физик Н. Бор [48]в 1913 г. для объяснения устойчивости атома ввел основные допущения (постулаты), которые легли в основу теории атома Бора, явившейся предшественницей квантовой механики.

Теория Бора является первой попыткой аналитического описания закономерностей строения атома и спектра его излучения и дает хорошее согласование с экспериментом только для атома водорода и водородоподобных атомов.

В основе теории два постулата:

Первый постулат существования в атоме стационарных состояний (орбит движения электронов), не изменяющихся во времени без внешнего воздействия:

В атоме существует ряд дискретных стационарных состояний, которым соответствуют определенные значения энергии атома. В стационарном состоянии атом не излучает и не поглощает энергии.

Дискретные стационарные состояния в теории Бора отбираются с помощью "правила квантования орбит": момент импульса[49] электрона на стационарной орбите кратен постоянной Планка:

mvr = n 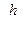 или  mvr = n ħ, (2)

где m = 9,1∙10^{-31 кг – масса электрона,}

v – скорость электрона на орбите,

r – радиус орбиты,

h = 6,63∙10^-34 Дж∙с – постоянная М. Планка,

ħ = 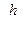= 1,05∙10^-34 Дж∙с

n = 1,2,3… - главное квантовое число.

Второй постулат испускания или поглощения одного кванта энергии при переходе атома из одного стационарного состояния в другое стационарное состояние.

При переходе атома из одного стационарного состояния в другое атом излучает и поглощает квант энергии ε = hν , равный разности энергий двух стационарных состояний:

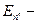
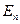
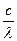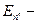
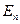hν = или h  = . (3)             

Теория Бора позволяет рассчитать параметры электрона в атоме (радиус орбиты, скорость, энергию).

r = 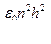; v = 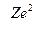  ; Е_полн. = – .

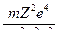Радиус орбиты. Полагаем, что из атома удалены все электроны, кроме одного; и электрон вращается по круговой орбите вокруг неподвижного ядра, тогда

заряд ядра атома q = Z|e|,

где |е| = 1,6∙10^-19 Кл - элементарный заряд,

Z - порядковый номер химического элемента в периодической таблице элементов Д.И. Менделеева.

Между положительно заряженным ядром (заряд q₁ = Z|e|) и электроном (модуль заряда q₂ = |e|) действует сила электростатического взаимодействия, которая согласно закону Кулона[50] может быть представлена:

F = 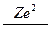, где

r – радиус орбиты,

ε₀ = 8,85∙10^-12 Ф/м – электрическая постоянная.

C другой стороны, так как электрон движется по окружности, следовательно, он обладает центростремительным (нормальным) ускорением

а =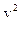

Согласно второму закону Ньютона: F = ma.

Значит:

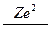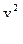= m . (4)

С помощью правила квантования орбит можно исключить скорость из формулы (2) и получить выражения для возможных радиусов орбит:

r = 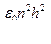. (5)

Скорость электрона в водородоподобном атоме. Используя формулу (4), можно получить выражение для расчета скоростей движения электрона по соответствующим орбитам:

v = 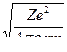 (6,а)

Если учесть формулу (5), то получим зависимость скорости от главного квантового числа

v = 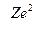  (6,б) .

Энергия электрона в водородоподобном атоме. Полная энергия электрона складывается из кинетической

К =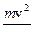            

и потенциальной[51]

    U = – 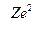 энергий. Учитывая выражение (6,а), получим:

Е_полн. = 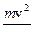 –  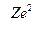= – 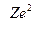. (7)                                 

Если воспользоваться формулой (4), то увидим, что полная энергия зависит от квантового числа:

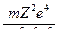Е_полн. = – . (8)

По второму постулату Бора при переходе электрона с орбиты (3):

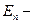
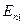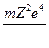
hν = = 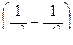, следовательно,

ν = 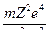 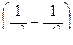= Z²R_ν 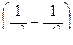, где

R_ν = 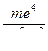 = 3,29∙10¹⁵ с^-1 – постоянная Ридберга.

Или

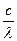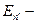
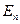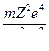
h  = =  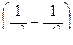, следовательно,

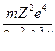
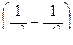 =  = Z²R_λ 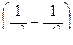, (9)

где

R_λ = 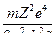= 1,097∙10⁷ м^-1.

Из формул (5), (6,б), (8) видно, что для электрона в атоме (ионе) радиусы орбит, скорости и энергии в стационарных состояниях могут принимать только дискретные значения, определяемые квантовым числом n.

Атом водорода (Z = 1) имеет наиболее простой линейчатый спектр излучения.

Опыт Франка и Герца[52] 1914 г. – подтверждает существование дискретных энергетических уровней атома (квантование энергии).

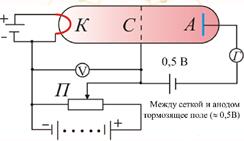
В трубке, заполненной парами ртути под не­большим давлением (~ 1ммрт. ст.), имелись три элек­трода: катод К, сетка С и анод А. Электроны, выле­тавшие из катода вследствие термоэлектронной эмиссии, ускорялись разностью потенциалов U , приложенной между катодом и сеткой.

Эту разность потенциалов можно было плавно менять с помощью потенциометра П.

Между сеткой и анодом создавалось слабое электрическое поле
(разность потенциалов порядка 0,5 В), тормозившее движение электронов к аноду.

Исследовалась зависимость силы тока I в цепи анода от напряжения U между катодом и сеткой. Сила тока измерялась гальвано­метром Г, напряжение — вольтметром V .

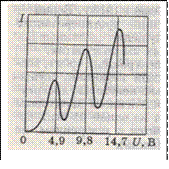
Полученные результаты представлены на рис. Видно, что сила тока вначале монотонно возрастала, достигая максимума при U = 4,9 В, после чего с дальнейшим увеличением U резко падала, достигая минимума, и снова начинала ра­сти. Максимумы силы тока повторялись при U , равном 9,8; 14,7 В и т. д.).

Такой ход кривой объясняется тем, что вследствие дис­кретности энергетических уровней атомы могут восприни­мать энергию только порциями: 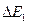=  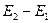либо 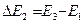 и т.д.

До тех пор, пока энергия электрона меньше 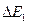 соударения между электроном и атомом ртути носят упру­гий характер, причем, поскольку масса электрона во много раз меньше массы атома ртути, энергия электрона при столкновениях практически не изменяется. Часть элек­тронов попадает на сетку, остальные же, проскочив через сетку, достигают анода, создавая ток в цепи гальванометра Г. Чем больше скорость, с которой электроны достигают сетки (чем больше U ), тем больше доля электронов, про­скочивших через сетку, и тем, следовательно, больше сила тока I.

Когда энергия, накапливаемая электроном в промежут­ке катод-сетка, достигает значения 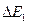 соударения перестают быть упругими - электроны при ударах об атомы передают им энергию  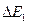и продолжают затем двигаться с меньшей скоростью. Поэтому число электро­нов, достигающих анода, уменьшается. Например, при U = 5,3 В электрон сообщает атому энергию, соответству­ющую 4,9 В (первый потенциал возбуждения атома ртути), и продолжает двигаться с энергией 0,4 эВ. Если даже та­кой электрон окажется между сеткой и анодом, он не смо­жет преодолеть задерживающее напряжение 0,5 В и будет возвращен обратно на сетку.

Атомы, получившие при соударении с электронами энергию 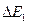, переходят в возбужденное состояние, из ко­торого они спустя время порядка 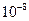с возвращаются в основное состояние, излучая фотон с частотой .

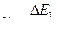При напряжении, превышающем 9,8 В, электрон на пути катод-анод может дважды претерпеть неупругое со­ударение с атомами ртути, теряя при этом энергию 9,8 эВ, вследствие чего сила тока снова начнет уменьшаться. При еще большем напряжении возможны трехкратные не­упругие соударения электронов с атомами, что приводит к возникновению максимума при U = 14,7 В, и т. д.

При достаточном разрежении паров ртути и соответ­ствующем ускоряющем напряжении электроны за время до столкновения с атомами могут приобретать скорость, достаточную для перевода атома в состояние с энергией .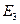

6.24. На рисунке изображены стационарные орбиты атома водорода согласно модели Бора, а также условно изображены переходы электрона с одной стационарной орбиты на другую, сопровожда-ющиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, в инфракрасной – серию Пашена. Какой переход соответствует наибольшей частоте кванта в серии Лаймана?

6.25.Определите длину волны спектральной линии, соответст­вующую переходу электрона в атоме водорода с шестой боровской орбиты на вторую. К какой серии относится эта линия и которая она по счету? [0,41 мкм; четвертая линия серии Бальмера]

6.26.Определите длину волны, соответствующую второй спек­тральной линии в серии Пашена.

6.27.Определите максимальную и минимальную энергии фото­на в видимой серии спектра водорода (серии Бальмера). [3,41 эВ; 1,89 эВ]

6.28.Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на вто­рой. [1,89 эВ]

6.29.Определите частоту света, излучаемого возбужденным атомом водорода, при переходе электрона на второй энергетический уровень, если радиус орбиты электрона изменился в 9 раз.

6.30.Определите энергию ионизации атома водорода и найдите энергию фотона, соответствующую самой длинно­волновой линии серии Лаймана.     [13,6 эВ; 10,2 эВ]

6.31.Определите первый потенциал возбуждения атома водо­рода.

6.32.Определите работу, которую необходимо совершить, чтобы удалить электрон со второй боровской орбиты атома водорода за пределы притяжения его ядром. [5,45∙10^-19 Дж]

6.33.Электрон выбит из атома водорода, находящегося в ос­новном состоянии, фотоном энергии 17,7 эВ. Определите скорость электрона за пределами атома. [2,49 Мм/с]

6.34.Определите, какая энергия требуется для полного отрыва электрона от ядра однократно ионизованного атома гелия, если: 1) электрон находится в основном состоянии; 2) электрон находится в состоянии, соответствующем главному квантовому числу   3. [1) 54,4 эВ; 2) 6,04 э B]

6.35. Определите работу, которую необходимо совершить, чтобы удалить электрон со второй боровской орбиты атома водорода за пределы притяжения его ядром. [0,006 нм; 0,009 нм]