Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Если число экспериментов велико, то составляются корреляционные таблицы. Для этого среди результатов эксперимента выбираются x_min, x_max, y_min, y_max. Интервал [x_min, x_{ma )}] возможных значений X делим с шагом h ₁ на n частичных интервалов, Интервал [y_min,y_max] для Y делим с шагом h ₂ на m частичных интервалов. Границы интервалов по X записываются в 1-ый столбец, по Y - в 1-ую строку.

Для каждой пары (x_i, y_i) определяем в какую строку попало значение x_i и в какой столбец y_i. В клетку, расположенную на пересечении найденной строки и столбца, ставим палочку (или точку) . Операцию проводим для всех пар. Подчитываем число палочек (точек) в каждой клетке и записываем полученное число в клетку. Просуммируем числа, стоящие в 1- ой строке, получим частоту 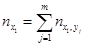- число пар (x_i,y_i), у которых первая координата попала в первый частичный интервал. Проведём суммирование по всем остальным строкам, полученные числа 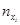заносим в последний столбец.

 

Таблица 7

Y,V   X, U	[y0, y1) y1*, v1	[y1, y2) y2*, v2	……	[yj1,yj)  yj*, vj C2	……	[ym-1, ym) ym*, vm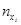
[x0, x1) x1*, u1			……		……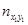
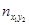
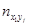
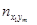
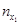
[x1, x2) x2*, u2			……		……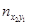
………	………	………	……	………	……	…………	…………
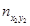
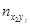
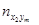
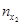
[xi-1,xi) C1, xi*, ui			……		……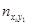
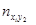
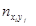
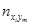
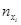
[xn1,xn) xn*,un			……		……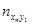
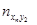
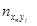
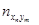
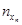
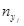
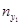
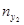
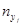
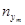
			……		……		N

Просуммируем величины, которые стоят в первом столбце. Получим частоту 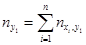- число пар (x_i, y_i), у которых y попадает в первый интервал. Найдём суммы по всем столбцам. Полученное значение запишем в последнюю строку. Суммы полученных значений равны N:

 

 

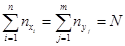
По виду корреляционной таблице можно судить о виде корреляционной зависимости.

Вычислим середины частичных интервалов

 

;

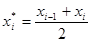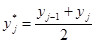
i =1,…, n ; j =1,…, m .

 

Внесем найденные значения в корреляционную таблицу. По таблице вычислим оценки математических ожиданий и дисперсий

 

; ;

; ;

; ;

.

 

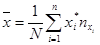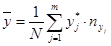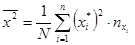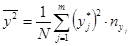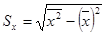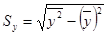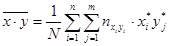Коэффициент линейной корреляции определяются по формуле:

 

.

 

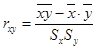Для простоты вычислений обычно используют замену переменных:

 

; ;

 

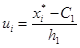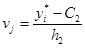где С₁ и С₂ – значения x_i ^* и y_j ^* соответствующие максимальной частоте 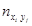. Желательно, чтобы клетка с данной частотой находилась в середине таблицы. Точку (С₁,С₂) называют ложным нулем. Переменные U и V – принимают значения: 0; ±1; ±2,…

 

, , ,

; .

 

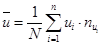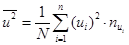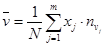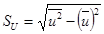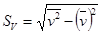При вычислениях используем, что

 

; .

 

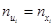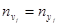Коэффициент корреляции вычисляется по формуле:

 

.

 

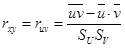Вернемся к исходным переменным:

 

; ;

; .

 

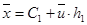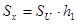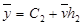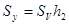Уравнения регрессии:

 

; .

 

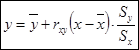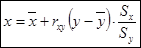Графики функций пересекаются в точке .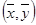

Пример:

Даны результаты 78 экспериментов:

X	Y	X	Y	X	Y	X	Y
73	-291	57	-219	61	-241	68	-264
69	-270	71	-281	62	-243	62	-240
72	-279	66	-262	63	-245	70	-277
72	-282	76	-302	71	-282	70	-279
65	-254	70	-275	65	-252	65	-253
67	-264	68	-267	70	-276	70	-275
56	-216	74	-290	70	-276	63	-248
70	-276	68	-266	63	-246	63	-243
63	-248	71	-283	73	-284	67	-264
64	-253	60	-237	68	-271	68	-267
70	-276	56	-222	59	-227	55	-213
67	-262	71	-281	64	-256	56	-218
60	-234	68	-269	79	-309	58	-223
80	-313	66	-257	77	-300	70	-278
71	-278	60	-235	78	-310	59	-236
74	-292	70	-275	66	-255	68	-263
68	-271	69	-276	63	-252	69	-268
65	-256	72	-282	69	-274	63	-243
73	-291	70	-277	74	-291	70	-271
63	-243	69	-270

 

Начало первого интервала x₀ = 53, y₀ = –321;

Длина интервала h₁ = 5, h₂ = 17.    

1. Построить корреляционное поле для 4-ых столбцов X и Y и методом “натянутой нити” найти линейные функции регрессии.

2. Составить корреляционную таблицу. Вычислить коэффициент линейной корреляции, найти уравнения регрессий и построить их графики.

3. Проверить гипотезу о незначимости коэффициента корреляции.

Решение.

1. По последним столбцам X и Y находим:

x_min=55; y_min=-279;

x_max=70; y_max=-213;

На осях отображаем тот промежуток, где находятся значения X и Y. Представляя в виде точек пары чисел (x₁; y_j) строим корреляционное поле:

 

 

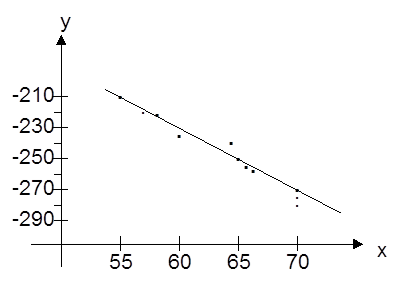
Используя метод “натянутой нити”, проведём прямую. На прямой выберем две точки (57, -220) и (69, -270), расположенные достаточно далеко друг от друга.. Подставляя значения в функцию y=ax+b, получим систему уравнений относительно a и b.

 

 ,

 

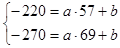Получим решение a = - 4,17; b = 17,69. Уравнение линейной регрессии имеет вид: y = - 4,17 x + 17,69.

2. Найдём минимальные и максимальные значения X и Y среди результатов эксперимента:

x_min=55; y_min=-313; x_max=80; y_max=-213;

Составим корреляционную таблицу с шагом h₁=5 по X и h₂=17 по Y. Учитываем, что левая граница входит в интервал, а правая нет.

Клетка в шапке сверху содержит границы интервала по Y [y_j, y_j+1], значение середины интервала y_j^* и значение середины интервала для условной переменной V. Клетка в шапке слева содержит границы интервала по X [x_i, x_i+1], значение середины интервала x_i^* и значение середины интервала для условной переменной U.

Произвольная клетка таблицы содержит число результатов 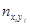, попавших в соответствующие интервалы. В нижней строке записываются суммы чисел в столбцах. В крайнем левом столбце – суммы чисел в строках.

 

Таблица 8.

Y,V     X,U	[321,-304) -312,5; -2	[304,-287) -295,5; -1	[287,-270) -278,5; 0	[270,-253) -261,5;  1	[253,-236) -244,5;  2	[236,-219) -227, 5; 3	[219,-202) -210,5 ; 4	nx nu
[53,58) 55,5;-3						. 1	. . . . 4	5
[58,63) 60,5;-2					. . . . 4	. . . . 5		9
[63,68) 65,5;-1				. . . . 9	. . . . . 11			20
[68,73) 70,5;0		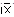	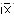.. 24	. . . . 9				33
[73,78) 75,5;1		. . . . 7	.  1					8
[78,83) 80,5;2	. . . 3							3
ny, nv	3	7	25	18	15	6	4	78

 

 Переход к условным вариантам.

 

; ;

 

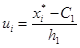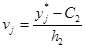C₁=70,5; С₂=-278,5 – координаты клетки с максимальным числом результатов экспериментов.

 

, ,…, ;

, ,…, ;

 

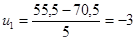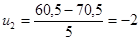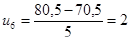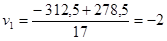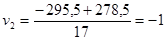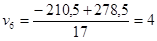Вычисляем средние:

 

.

 

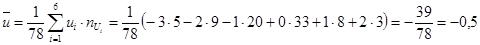
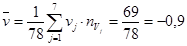Вычислим среднее квадратов:

 

.

 

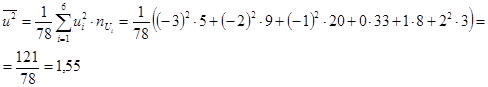
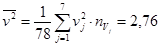Вычислим среднее квадратическое отклонение:

; ;

;

 

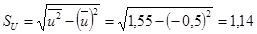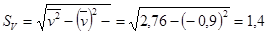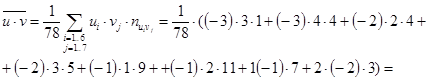
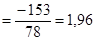Коэффициент корреляции:

 

;

 

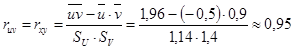Находим статистические характеристики X, Y:

 

; ;

; ;

 

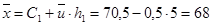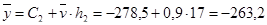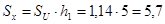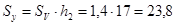Уравнение регрессии:

 

; ;

;

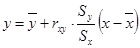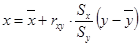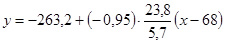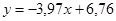 (I);

;

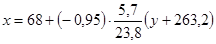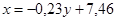 (II)

 

 

Определим координаты двух точек для каждого графика:

 

X	60	75
Y	-231,4	-291

Y	-300	-220
X	76,46	58,06

 

 

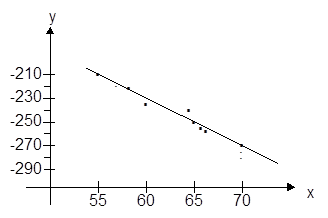
Графики пересеклись в точке M(68; -263,2)

 

3. Проверим гипотезу о незначимости коэффициента корреляции. Наблюдаемое значение критерия:

 

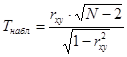; N = max { n , m };

n , m – число частичных интервалов по X и Y.

n = 6; m = 7; N = 7.

 

;

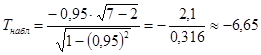T _кр = T (0,05; N -2)= T (0,05; 5)=2,57 – по таблице распределения Стьюдента.

Так как | T _набл |=6,65>2,57, то гипотеза отвергается, следовательно r _xy значим.

 

Вывод

 

В курсовую работу вошли задачи, решаемые на стадии предварительного эксперимента. При решении этих задач использованы идеи и методы математической статистики, в частности ее разделы - оценивание параметров и проверка статистических гипотез. Используя эти методы, проверяются следующие гипотезы: о воспроизводимости результатов эксперимента, о виде распределения результатов эксперимента, о наличии корреляционных связей между факторами и переменной состояния и др.

 

Список литературы

 

1.Егоров А.Е., Азаров Г.Н., Коваль А.В. Исследование устройств и систем автоматики методом планирования эксперимента. – К.: Вища школа, 1986.

2.Бондарь А.Г., Статюха Г.А. Планирование эксперимента в химической технологии. – К.: Вища школа, 1978.

3.Кафаров В.В. Методы кибернетики в химии и химической технологии. – М.: Химия, 1971.

4.Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Высшая школа, 1991.

5.Твердохлебов Г.Н., Бродский А.Л., Старобина Е.К., Кутакова Д.А. Методические указания по математическим методам анализа и планирования эксперимента для студентов всех химических специальностей. -Ворошиловград, 1985.

 

Приложение 1

(таблица значений функции Лапласа Ф(х))

 

(Таблица значений функции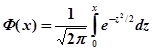  

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0.00	0.0000	0.22	0.0871	0.44	0.1700	0.66	0.2454
0.01	0.0040	0.23	0.0910	0.45	0.1736	0.67	0.2486
0.02	0.0080	0.24	0.0948	0.46	0.1772	0.68	0.2517
0.03	0.0120	0.25	0.0987	0.47	0.1808	0.69	0.2549
0.04	0.0160	0.26	0.1026	0.48	0.1844	0.70	0.2580
0.05	0.0199	0.27	0.1064	0.49	0.1879	0.71	0.2611
0.06	0.0239	0.28	0.1103	0.50	0.1915	0.72	0.2642
0.07	0.0279	0.29	0.1141	0.51	0.1950	0.73	0.2673
0.08	0.0319	0.30	0.1179	0.52	0.1985	0.74	0.2703
0.09	0.0359	0.31	0.1217	0.53	0.2019	0.75	0.2734
0.10	0.0398	0.32	0.1255	0.54	0.2054	0.76	0.2764
0.11	0.0438	0.33	0.1293	0.55	0.2088	0.77	0.2794
0.12	0.0478	0.34	0.1331	0.56	0.2123	0.78	0.2823
0.13	0.0517	0.35	0.1368	0.57	0.2157	0.79	0.2852
0.14	0.0557	0.36	0.1406	0.58	0.2190	0.80	0.2881
0.15	0.0596	0.37	0.1443	0.59	0.2224	0.81	0.2910
0.16	0.0636	0.38	0.1480	0.60	0.2257	0.82	0.2939
0.17	0.0675	0.39	0.1517	0.61	0.2291	0.83	0.2967
0.18	0.0714	0.40	0.1554	0.62	0.2324	0.84	0.2995
0.19	0.0753	0.41	0.1591	0.63	0.2357	0.85	0.3023
0.20	0.0793	0.42	0.1628	0.64	0.2389	0.86	0.3051

0.88	0.3106	1.14	0.3729	1.40	0.4192	1.66	0.4515
0.89	0.3133	1.15	0.3749	1.41	0.4207	1.67	0.4525
0.90	0.3159	1.16	0.3770	1.42	0.4222	1.68	0.4535
0.91	0.3186	1.17	0.3790	1.43	0.4236	1.69	0.4545
0.92	0.3212	1.18	0.3810	1.44	0.4251	1.70	0.4554
0.93	0.3238	1.19	0.3830	1.45	0.4265	1.71	0.4564
0.94	0.3264	1.20	0.3849	1.46	0.4279	1.72	0.4573
0.95	0.3289	1.21	0.3869	1.47	0.4292	1.73	0.4582
0.96	0.3315	1.22	0.3883	1.48	0.4306	1.74	0.4591
0.97	0.3340	1.23	0.3907	1.49	0.4319	1.75	0.4599
0.98	0.3365	1.24	0.3925	1.50	0.4332	1.76	0.4608
0.99	0.3389	1.25	0.3944	1.51	0.4345	1.77	0.4616
1.00	0.3413	1.26	0.3962	1.52	0.4357	1.78	0.4625
1.01	0.3438	1.27	0.3980	1.53	0.4370	1.79	0.4633
1.02	0.3461	1.28	0.3997	1.54	0.4382	1.80	0.4641
1.03	0.3485	1.29	0.4015	1.55	0.4394	1.81	0.4649
1.04	0.3508	1.30	0.4032	1.56	0.4406	1.82	0.4656
1.05	0.3531	1.31	0.4049	1.57	0.4418	1.83	0.4664
1.06	0.3554	1.32	0.4066	1.58	0.4429	1.84	0.4671
1.07	0.3577	1.33	0.4082	1.59	0.4441	1.85	0.4678
1.08	0.3599	1.34	0.4099	1.60	0.4452	1.86	0.4686
1.09	0.3621	1.35	0.4115	1.61	0.4463	1.87	0.4693
1.10	0.3643	1.36	0.4131	1.62	0.4474	1.88	0.4699
1.11	0.3665	1.37	0.4147	1.63	0.4484	1.89	0.4706
1.12	0.3686	1.38	0.4162	1.64	0.4495	1.90	0.4713
1.13	0.3708	1.39	0.4177	1.65	0.4505	1.91	0.4719

 

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
1.92	0.4726	2.18	0.4854	2.52	0.4941	2.84	0.4977
1.93	0.4732	2.20	0.4861	2.54	0.4945	2.86	0.4979
1.94	0.4738	2.22	0.4868	2.56	0.4948	2.88	0.4980
1.95	0.4744	2.24	0.4875	2.58	0.4951	2.90	0.4981
1.96	0.4750	2.26	0.4881	2.60	0.4953	2.92	0.4982
1.97	0.4756	2.28	0.4887	2.62	0.4956	2.94	0.4984
1.98	0.4761	2.30	0.4893	2.64	0.4959	2.96	0.4985
1.99	0.4767	2.32	0.4898	2.66	0.4961	2.98	0.4986
2.00	0.4772	2.34	0.4904	2.68	0.4963	3.00	0.49865
2.02	0.4783	2.36	0.4909	2.70	0.4965	3.20	0.49931
2.04	0.4793	2.38	0.4913	2.72	0.4967	3.40	0.49966
2.06	0.4803	2.40	0.4918	2.74	0.4969	3.60	0.499841
2.08	0.4812	2.42	0.4922	2.76	0.4971	3.80	0.499928
2.10	0.4821	2.44	0.4927	2.78	0.4973	4.00	0.499968
2.12	0.4830	2.46	0.4931	2.80	0.4974	4.50	0.499997
2.14	0.4838	2.48	0.4934	2.82	0.4976	5.00	0.499997
2.16	0.4846	2.50	0.4938

 

 

Приложение 2

(таблица критических точек критерия Пирсона)

c² – распределение (распределение Пирсона)

f	b
	0.05	0.01	0.005
1 2 3 4 5 6 7 8 10 12 14 16 18 20 22 24 26 28 30	3.84 5.99 7.81 9.49 11.1 12.6 14.1 15.5 18.3 21.0 23.7 26.3 28.9 32.4 33.9 36.4 38.9 41.3 43.8	6.63 9.21 11.3 13.3 15.1 16.8 18.5 20.1 23.2 26.2 29.1 32.0 34.8 37.6 40.3 43.0 45.6 48.3 50.9	7.88 10.6 12.8 18.5 20.5 22.5 24.3 26.1 29.6 32.9 36.1 39.3 42.3 45.3 48.3 51.2 54.1 56.9 59.7

 

 

Приложение 3

(таблица критических точек критерия Стьюдента)

(t – критерий)

ft	a
	0.05	0.01	0.005
1 2 3 4 5 6 7 8 9 10 12 14 16 18 20 22 24 26 30 ¥	12.71 4.30 3.18 2.78 2.57 2.45 2.36 2.31 2.26 2.23 2.18 2.14 2.12 2.11 2.09 2.07 2.06 2.06 2.04 1.6	63.66 9.92 5.84 4.60 4.03 3.71 3.50 3.36 3.25 3.17 3.06 2.98 2.92 2.88 2.84 2.82 2.80 2.78 2.75 2.56	127.3 14.1 7.45 5.60 4.77 4.32 4.03 3.83 3.69 3.58 3.43 3.33 3.25 3.19 3.15 3.12 3.09 3.07 3.03 2.81

 

 

Приложение 4

(таблица критических точек критерия Фишера)

(F – распределение для уровня значимости q=0.05)

f2	f1
	1	2	3	4	5	8	12	24	¥
1 2 3 4 5 6 7 8 10 12 16 20 60 ¥	164 18.5 10.1 7.71 6.61 5.99 5.50 5.32 4.96 4.75 4.49 4.35 4.00 3.84	199 19.0 9.55 6.94 5.79 5.14 4.74 4.46 4.10 3.88 3.63 3.49 3.15 2.99	215 19.2 9.28 6.59 5.41 4.76 4.35 4.07 3.71 3.49 3.24 3.10 2.76 2.60	224 19.2 9.12 6.39 5.19 4.53 4.12 3.84 3.48 3.26 3.01 2.87 2.52 2.37	234 19.3 8.94 6.16 4.95 4.28 3.87 3.58 3.22 3.00 2.74 2.60 2.25 2.09	239 19.4 8.84 6.04 4.82 4.15 3.73 3.44 3.07 2.85 2.59 2.45 2.10 1.94	243 19.4 8.74 5.91 4.68 4.00 3.57 3.28 2.91 3.69 2.42 2.28 1.92 1.75	249 19.4 8.64 5.77 4.53 3.84 3.41 3.12 2.74 2.50 2.24 2.08 1.70 1.52	254 19.5 8.53 5.63 4.36 3.67 3.23 2.93 2.54 2.30 2.01 1.84 1.39 1.00

Примечание. f₁ – число степеней свободы большей дисперсии, f₂ – число степеней свободы меньшей дисперсии.

 

Приложение 5

(таблица критических точек критерия Кохрена)

(G- критерий для уровня значимости q=0.05)

få	fu
	1	2	3	4	5	7	9	16	36	¥
2 3 4 5 6 7 8 9 10 15 20 30 60 120	0.998 0.967 0.906 0.841 0.781 0.727 0.680 0.638 0.602 0.471 0.389 0.293 0.174 0.100	0.975 0.871 0.768 0.684 0.616 0.561 0.516 0.478 0.445 0.335 0.270 0.198 0.113 0.063	0.939 0.798 0.684 0.598 0.532 0.480 0.438 0.403 0.373 0.276 0.220 0.159 0.090 0.050	0.906 0.746 0.629 0.544 0.480 0.431 0.391 0.358 0.331 0.242 0.192 0.138 0.076 0.042	0.877 0.707 0.589 0.506 0.445 0.397 0.360 0.329 0.303 0.220 0.174 0.124 0.068 0.037	0.833 0.653 0.536 0.456 0.398 0.354 0.318 0.290 0.267 0.191 0.150 0.106 0.058 0.031	0.801 0.617 0.502 0.424 0.368 0.326 0.293 0.266 0.244 0.174 0136 0.096 0.052 0.028	0.734 0.547 0.437 0.364 0.314 0.276 0.246 0.223 0.203 0.143 0.111 0.077 0.041 0.022	0.660 0.475 0.372 0.307 0.261 0.228 0.202 0.182 0.166 0.114 0.088 0.060 0.032 0.016	0.500 0.333 0.250 0.200 0.167 0.143 0.125 0.111 0.100 0.067 0.050 0.033 0.017 0.008

Примечание. f_u – число степеней свободы числителя; f_å -- число степеней свободы знаменателя.

 

 

Приложение 6

(таблица критических точек r ‑ критерия)

(r – критерий для уровней значимости q={0.05;0.01})

f	q=0.05	q=0.01
2 3 4 5 6 7 8 9 10 12 14 16 18 20 25 30 35 40 45 50	1.41 1.69 1.87 2.00 2.09 2.17 2.24 2.29 2.34 2.43 2.49 2.55 2.60 2.64 2.73 2.80 2.86 2.91 2.96 2.99	1.41 1.72 1.96 2.13 2.26 2.37 2.46 2.54 2.61 2.71 2.80 2.87 2.93 2.98 3.09 3.17 3.24 3.29 3.34 3.38