Статистической называют гипотезу о виде неизвестного распределения или о параметрах известного распределения.

Например, гипотеза H ₀ - случайная величина распределена по нормальному закону.

Нулевой (основной) называется выдвинутая гипотеза H ₀.

Альтернативной (конкурирующей) называется гипотеза, противоречащая основной (конкурирующих гипотез может быть несколько).

Например, основная гипотеза - математическое ожидание случайной величины Y равно 5

H ₀ : M_y =5,

конкурирующие:

H ₁ :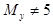

H ₂ :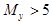

H ₃ :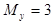

Статистическим критерием (К) называется случайная величина, точное или приближённое распределение, которой известно и которая служит для проверки справедливости нулевой гипотезы.

Множество возможных значений критерия делится на две непересекающихся области:

1) значения, при которых нулевая гипотеза справедлива (область принятия гипотезы).

2) значения, при которых нулевая гипотеза отвергается (критическая область).

Критическая область может быть односторонней (левосторонней, правосторонней) или двусторонней.

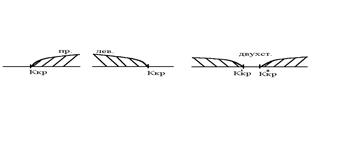
Рис.1. Виды критических областей: правосторонняя, левосторонняя и двусторонняя.

Точка К_кр, отделяющая критическую область от области принятия гипотезы, называется критической точкой.

Чтобы определить критическую область, выбирают число q-уровень значимости. q - вероятность того, что при справедливости нулевой гипотезы значение критерия К попадает в критическую область. Тогда для правосторонней критической области К_кр определяется из условия:

P { K > K_kp } = q .

Значение критерия табулировано, т. е. K_kp можно найти по таблице распределения критических точек в зависимости от уровня значимости q и числа степеней свободы f . -Наблюдаемое значение критерия K _набл определяется по результатам эксперимента.

Если K _набл < K_kp, то гипотеза H ₀ принимается. Если K _набл > K_kp, то H ₀ отвергается, а принимается конкурирующая гинотеза H ₁.

Для левосторонней критической области критическая точка определяется из условия:

P { K < K_kp } = q .

Для двухсторонней:

P { K < K ’ _kp } + P { K > K ” _kp } = q .

Если двусторонняя область симметрична относительно начала координат, то:

P { K < K ’ _kp } = .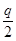

Так как наблюдаемое значение критерия определялось по результатам эксперимента, то К_набл-случайная величина и, следовательно, могут возникать ошибки при принятии гипотезы. Различают ошибки первого и второго рода. К ошибкам первого рода относят те, при которых отвергается правильная гипотеза. К ошибкам второго рода, относят те, при которых принимается неправильная гипотеза. Допустимой вероятностью ошибки первого рода является q-уровень значимости. Однако. если уменьшать q, то возрастает вероятность принятия неверной гипотезы, т. е. вероятность ошибок второго рода. Если справедлива гипотеза H ₁, то это считается доказанным, если справедлива гипотеза H ₀-то говорят, что результаты эксперимента не противоречат нулевой гипотезы. Для того чтобы считать H ₀ доказанной нужно или вновь повторить эксперимент или проверить гипотезу с помощью других критериев.