Статистическая проверка гипотез

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Содержание

Введение

Статистическая проверка гипотез

Статистическая гипотеза. Статистический критерий. Ошибки, возникающие при проверке гипотез

2. Порядок проверки статистических гипотез

3. Проверка однородности результатов эксперимента в целях исключения грубых ошибок

4. Проверка гипотезы о воспроизводимости опытов

5. Проверка гипотезы о нормальном распределении ошибок эксперимента

6. Проверка гипотезы о виде распределения. ( Критерий согласия Пирсона )

6.1 Расчёт теоретических частот для нормального распределения

7.Проверка гипотезы о согласованности мнений экспертов (априорное ранжирование переменных)

8. Уравнение линейной регрессии. Коэффициент корреляции. Проверка гипотезы о значимости коэффициента корреляции

Метод наименьших квадратов

Проверка незначимости коэффициента корреляции

Использование корреляционной таблицы для вычисления коэффициента корреляции

Вывод

Список литературы

Приложения

Введение

Тема курсовой работы «Статистическая проверка гипотез».

К важнейшим направлениям научно-технического прогресса относятся автоматизация производства, широкое применение компьютеров и роботов, создание гибких автоматизированных устройств и т.д. Во всех этих направлениях ведущая роль принадлежит электронике.

При создании электронной и электромеханической аппаратуры основные трудозатраты приходятся на ее настройку, снятие характеристик и испытания. При этом нередко используется малоэффективный традиционный метод однофакторного эксперимента, недостаточно внимания уделяется организации и планированию эксперимента и вероятностно-статистическому анализу получаемых данных. Чтобы повысить производительность труда в данной области, специалистам необходимо знать основы математической теории эксперимента и успешно применить ее на практике.

Цель работы – ознакомится со статистической проверкой гипотез, а именно:

о воспроизводимости результатов эксперимента, о виде распределения результатов эксперимента, о наличии корреляционных связей между факторами и переменной состояния и др., рассмотрении практических примеров.

Статистическая проверка гипотез

Порядок проверки статистических гипотез

1) Выбор нулевой и альтернативной гипотез H ₀ и H ₁.

2) Выбор критерия K и уровня значимости q.

3) Вычисление K _набл по результатам эксперимента.

4) Поиск K_kp по таблице распределения критических точек для выбранного критерия.

5) Если K _набл попадает в критическую область, то принимается альтернативная гипотеза H ₁, если K _набл попадает в область принятия гипотезы, то принимается основная гипотеза H ₀.

Метод наименьших квадратов

Будем искать уравнение регрессии в виде линейной зависимости:

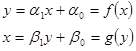
Коэффициенты a₀ и a₁ определяются из условия: сумма квадратов отклонений экспериментальных значений y от рассчитанных по уравнению регрессии должна быть минимальной.

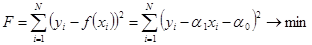
Для отыскания минимума составим систему уравнений

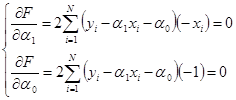
Решая эту систему, получаем значения коэффициентов:

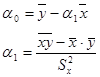
Обозначим через r_xy оценку коэффициента линейной корреляции:

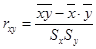Тогда коэффициенты регрессии определяются равенствами

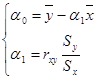
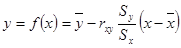- уравнение линейной регрессии.

Аналогичные вычисления для второго уравнения регрессии x = b ₁ y + b ₀ = g ( y ) дают следующие значения коэффициентов:

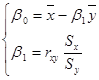Тогда уравнение регрессии имеет вид:

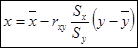Свойства коэффициента линейной корреляции:

1.Коэффициент линейной корреляции r_xy по абсолютной величине не превышает 1: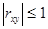

2.Если X и Y (случайные величины) независимы, то r_xy =0, обратное утверждение верно не всегда.

3.Если r_xy = ± 1, то величины X , Y связаны функциональной линейной зависимостью.

4.Если 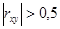, то зависимость X и Y строят в виде линейной функции. В случае 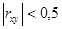рассматриваются другие виды зависимости, например, квадратичная зависимость, гиперболическая, логарифмическая:

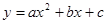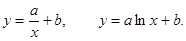
Вывод

В курсовую работу вошли задачи, решаемые на стадии предварительного эксперимента. При решении этих задач использованы идеи и методы математической статистики, в частности ее разделы - оценивание параметров и проверка статистических гипотез. Используя эти методы, проверяются следующие гипотезы: о воспроизводимости результатов эксперимента, о виде распределения результатов эксперимента, о наличии корреляционных связей между факторами и переменной состояния и др.

Список литературы

1.Егоров А.Е., Азаров Г.Н., Коваль А.В. Исследование устройств и систем автоматики методом планирования эксперимента. – К.: Вища школа, 1986.

2.Бондарь А.Г., Статюха Г.А. Планирование эксперимента в химической технологии. – К.: Вища школа, 1978.

3.Кафаров В.В. Методы кибернетики в химии и химической технологии. – М.: Химия, 1971.

4.Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Высшая школа, 1991.

5.Твердохлебов Г.Н., Бродский А.Л., Старобина Е.К., Кутакова Д.А. Методические указания по математическим методам анализа и планирования эксперимента для студентов всех химических специальностей. -Ворошиловград, 1985.

Приложение 1

(таблица значений функции Лапласа Ф(х))

(Таблица значений функции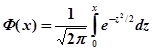

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0.00	0.0000	0.22	0.0871	0.44	0.1700	0.66	0.2454
0.01	0.0040	0.23	0.0910	0.45	0.1736	0.67	0.2486
0.02	0.0080	0.24	0.0948	0.46	0.1772	0.68	0.2517
0.03	0.0120	0.25	0.0987	0.47	0.1808	0.69	0.2549
0.04	0.0160	0.26	0.1026	0.48	0.1844	0.70	0.2580
0.05	0.0199	0.27	0.1064	0.49	0.1879	0.71	0.2611
0.06	0.0239	0.28	0.1103	0.50	0.1915	0.72	0.2642
0.07	0.0279	0.29	0.1141	0.51	0.1950	0.73	0.2673
0.08	0.0319	0.30	0.1179	0.52	0.1985	0.74	0.2703
0.09	0.0359	0.31	0.1217	0.53	0.2019	0.75	0.2734
0.10	0.0398	0.32	0.1255	0.54	0.2054	0.76	0.2764
0.11	0.0438	0.33	0.1293	0.55	0.2088	0.77	0.2794
0.12	0.0478	0.34	0.1331	0.56	0.2123	0.78	0.2823
0.13	0.0517	0.35	0.1368	0.57	0.2157	0.79	0.2852
0.14	0.0557	0.36	0.1406	0.58	0.2190	0.80	0.2881
0.15	0.0596	0.37	0.1443	0.59	0.2224	0.81	0.2910
0.16	0.0636	0.38	0.1480	0.60	0.2257	0.82	0.2939
0.17	0.0675	0.39	0.1517	0.61	0.2291	0.83	0.2967
0.18	0.0714	0.40	0.1554	0.62	0.2324	0.84	0.2995
0.19	0.0753	0.41	0.1591	0.63	0.2357	0.85	0.3023
0.20	0.0793	0.42	0.1628	0.64	0.2389	0.86	0.3051

0.88	0.3106	1.14	0.3729	1.40	0.4192	1.66	0.4515
0.89	0.3133	1.15	0.3749	1.41	0.4207	1.67	0.4525
0.90	0.3159	1.16	0.3770	1.42	0.4222	1.68	0.4535
0.91	0.3186	1.17	0.3790	1.43	0.4236	1.69	0.4545
0.92	0.3212	1.18	0.3810	1.44	0.4251	1.70	0.4554
0.93	0.3238	1.19	0.3830	1.45	0.4265	1.71	0.4564
0.94	0.3264	1.20	0.3849	1.46	0.4279	1.72	0.4573
0.95	0.3289	1.21	0.3869	1.47	0.4292	1.73	0.4582
0.96	0.3315	1.22	0.3883	1.48	0.4306	1.74	0.4591
0.97	0.3340	1.23	0.3907	1.49	0.4319	1.75	0.4599
0.98	0.3365	1.24	0.3925	1.50	0.4332	1.76	0.4608
0.99	0.3389	1.25	0.3944	1.51	0.4345	1.77	0.4616
1.00	0.3413	1.26	0.3962	1.52	0.4357	1.78	0.4625
1.01	0.3438	1.27	0.3980	1.53	0.4370	1.79	0.4633
1.02	0.3461	1.28	0.3997	1.54	0.4382	1.80	0.4641
1.03	0.3485	1.29	0.4015	1.55	0.4394	1.81	0.4649
1.04	0.3508	1.30	0.4032	1.56	0.4406	1.82	0.4656
1.05	0.3531	1.31	0.4049	1.57	0.4418	1.83	0.4664
1.06	0.3554	1.32	0.4066	1.58	0.4429	1.84	0.4671
1.07	0.3577	1.33	0.4082	1.59	0.4441	1.85	0.4678
1.08	0.3599	1.34	0.4099	1.60	0.4452	1.86	0.4686
1.09	0.3621	1.35	0.4115	1.61	0.4463	1.87	0.4693
1.10	0.3643	1.36	0.4131	1.62	0.4474	1.88	0.4699
1.11	0.3665	1.37	0.4147	1.63	0.4484	1.89	0.4706
1.12	0.3686	1.38	0.4162	1.64	0.4495	1.90	0.4713
1.13	0.3708	1.39	0.4177	1.65	0.4505	1.91	0.4719

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
1.92	0.4726	2.18	0.4854	2.52	0.4941	2.84	0.4977
1.93	0.4732	2.20	0.4861	2.54	0.4945	2.86	0.4979
1.94	0.4738	2.22	0.4868	2.56	0.4948	2.88	0.4980
1.95	0.4744	2.24	0.4875	2.58	0.4951	2.90	0.4981
1.96	0.4750	2.26	0.4881	2.60	0.4953	2.92	0.4982
1.97	0.4756	2.28	0.4887	2.62	0.4956	2.94	0.4984
1.98	0.4761	2.30	0.4893	2.64	0.4959	2.96	0.4985
1.99	0.4767	2.32	0.4898	2.66	0.4961	2.98	0.4986
2.00	0.4772	2.34	0.4904	2.68	0.4963	3.00	0.49865
2.02	0.4783	2.36	0.4909	2.70	0.4965	3.20	0.49931
2.04	0.4793	2.38	0.4913	2.72	0.4967	3.40	0.49966
2.06	0.4803	2.40	0.4918	2.74	0.4969	3.60	0.499841
2.08	0.4812	2.42	0.4922	2.76	0.4971	3.80	0.499928
2.10	0.4821	2.44	0.4927	2.78	0.4973	4.00	0.499968
2.12	0.4830	2.46	0.4931	2.80	0.4974	4.50	0.499997
2.14	0.4838	2.48	0.4934	2.82	0.4976	5.00	0.499997
2.16	0.4846	2.50	0.4938

Приложение 2

(таблица критических точек критерия Пирсона)

c² – распределение (распределение Пирсона)

f	b
f	0.05	0.01	0.005
1 2 3 4 5 6 7 8 10 12 14 16 18 20 22 24 26 28 30	3.84 5.99 7.81 9.49 11.1 12.6 14.1 15.5 18.3 21.0 23.7 26.3 28.9 32.4 33.9 36.4 38.9 41.3 43.8	6.63 9.21 11.3 13.3 15.1 16.8 18.5 20.1 23.2 26.2 29.1 32.0 34.8 37.6 40.3 43.0 45.6 48.3 50.9	7.88 10.6 12.8 18.5 20.5 22.5 24.3 26.1 29.6 32.9 36.1 39.3 42.3 45.3 48.3 51.2 54.1 56.9 59.7

Приложение 3

(таблица критических точек критерия Стьюдента)

(t – критерий)

f_t	a
f_t	0.05	0.01	0.005
1 2 3 4 5 6 7 8 9 10 12 14 16 18 20 22 24 26 30 ¥	12.71 4.30 3.18 2.78 2.57 2.45 2.36 2.31 2.26 2.23 2.18 2.14 2.12 2.11 2.09 2.07 2.06 2.06 2.04 1.6	63.66 9.92 5.84 4.60 4.03 3.71 3.50 3.36 3.25 3.17 3.06 2.98 2.92 2.88 2.84 2.82 2.80 2.78 2.75 2.56	127.3 14.1 7.45 5.60 4.77 4.32 4.03 3.83 3.69 3.58 3.43 3.33 3.25 3.19 3.15 3.12 3.09 3.07 3.03 2.81

Приложение 4

(таблица критических точек критерия Фишера)

(F – распределение для уровня значимости q=0.05)

f₂	f₁
f₂	1	2	3	4	5	8	12	24	¥
1 2 3 4 5 6 7 8 10 12 16 20 60 ¥	164 18.5 10.1 7.71 6.61 5.99 5.50 5.32 4.96 4.75 4.49 4.35 4.00 3.84	199 19.0 9.55 6.94 5.79 5.14 4.74 4.46 4.10 3.88 3.63 3.49 3.15 2.99	215 19.2 9.28 6.59 5.41 4.76 4.35 4.07 3.71 3.49 3.24 3.10 2.76 2.60	224 19.2 9.12 6.39 5.19 4.53 4.12 3.84 3.48 3.26 3.01 2.87 2.52 2.37	234 19.3 8.94 6.16 4.95 4.28 3.87 3.58 3.22 3.00 2.74 2.60 2.25 2.09	239 19.4 8.84 6.04 4.82 4.15 3.73 3.44 3.07 2.85 2.59 2.45 2.10 1.94	243 19.4 8.74 5.91 4.68 4.00 3.57 3.28 2.91 3.69 2.42 2.28 1.92 1.75	249 19.4 8.64 5.77 4.53 3.84 3.41 3.12 2.74 2.50 2.24 2.08 1.70 1.52	254 19.5 8.53 5.63 4.36 3.67 3.23 2.93 2.54 2.30 2.01 1.84 1.39 1.00

Примечание. f₁ – число степеней свободы большей дисперсии, f₂ – число степеней свободы меньшей дисперсии.

Приложение 5

(таблица критических точек критерия Кохрена)

(G- критерий для уровня значимости q=0.05)

f_å	f_u
f_å	1	2	3	4	5	7	9	16	36	¥
2 3 4 5 6 7 8 9 10 15 20 30 60 120	0.998 0.967 0.906 0.841 0.781 0.727 0.680 0.638 0.602 0.471 0.389 0.293 0.174 0.100	0.975 0.871 0.768 0.684 0.616 0.561 0.516 0.478 0.445 0.335 0.270 0.198 0.113 0.063	0.939 0.798 0.684 0.598 0.532 0.480 0.438 0.403 0.373 0.276 0.220 0.159 0.090 0.050	0.906 0.746 0.629 0.544 0.480 0.431 0.391 0.358 0.331 0.242 0.192 0.138 0.076 0.042	0.877 0.707 0.589 0.506 0.445 0.397 0.360 0.329 0.303 0.220 0.174 0.124 0.068 0.037	0.833 0.653 0.536 0.456 0.398 0.354 0.318 0.290 0.267 0.191 0.150 0.106 0.058 0.031	0.801 0.617 0.502 0.424 0.368 0.326 0.293 0.266 0.244 0.174 0136 0.096 0.052 0.028	0.734 0.547 0.437 0.364 0.314 0.276 0.246 0.223 0.203 0.143 0.111 0.077 0.041 0.022	0.660 0.475 0.372 0.307 0.261 0.228 0.202 0.182 0.166 0.114 0.088 0.060 0.032 0.016	0.500 0.333 0.250 0.200 0.167 0.143 0.125 0.111 0.100 0.067 0.050 0.033 0.017 0.008

Примечание. f_u – число степеней свободы числителя; f_å -- число степеней свободы знаменателя.

Приложение 6

(таблица критических точек r ‑ критерия)

(r – критерий для уровней значимости q={0.05;0.01})

f	q=0.05	q=0.01
2 3 4 5 6 7 8 9 10 12 14 16 18 20 25 30 35 40 45 50	1.41 1.69 1.87 2.00 2.09 2.17 2.24 2.29 2.34 2.43 2.49 2.55 2.60 2.64 2.73 2.80 2.86 2.91 2.96 2.99	1.41 1.72 1.96 2.13 2.26 2.37 2.46 2.54 2.61 2.71 2.80 2.87 2.93 2.98 3.09 3.17 3.24 3.29 3.34 3.38

Содержание

Введение

Статистическая проверка гипотез

Дата: 2019-05-28, просмотров: 159.

12 3 4 5 6 Следующая ⇒