После отсеивания незначимых факторов проверяется наличие корреляционных связей между факторами и между факторами и переменной состояния. Из статистики известно, что линейная связь между величинами X и Y оценивается с помощью коэффициента корреляции.
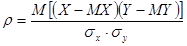
Пусть проведены N экспериментов, в результате которых получены следующие значения величин X и Y:
| X | x1,x2,............,xN |
| Y | y1,y2,............,yN |
Нанесём результаты экспериментов на координатную плоскость в виде точек, координатами которых является xi , y i , получим корреляционное поле
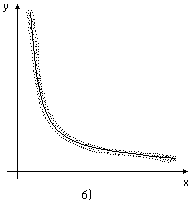
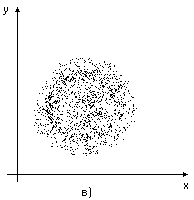
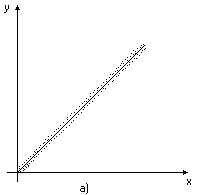
Рис.3. Корреляционное поле.
На рис.3а) – явно линейная зависимость между X и Y,
на рис.3б) –зависимость нелинейная,
на рис.3в) – зависимость между X и Y отсутствует.
Простейшим видом эмпирической формулы является линейная зависимость
Y = aX + b.
Функцию f(x) = ax + b называют линейной регрессией Y на X .
Существуют различные методы вычисления коэффициентов a и b: метод “натянутой нити”, метод сумм и метод наименьших квадратов.
Рассмотрим метод “натянутой нити”.
Нанесём результаты эксперимента на координатную плоскость (см. рис.4)) . Мысленно натянем нить таким образом, чтобы по обе стороны от неё оставалось приблизительно равное число точек, при этом суммы расстояний от точек до нити с обеих сторон должны быть одинаковы и минимальны.
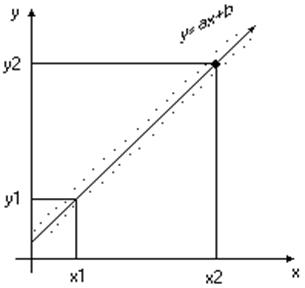 |
Рис.4. Метод ”натянутой нити”.
На прямой, совпадающей с направлением нити, выберем две точки с координатами (x1,y1) и (x2,y2). Подставим координаты точек в уравнение y=ax+b. Получим систему из двух уравнений с двумя неизвестными a и b и решаем её
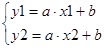
Составим уравнение y=ax+b, используя решение (a,b) системы.
Метод наименьших квадратов
Будем искать уравнение регрессии в виде линейной зависимости:
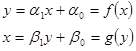
Коэффициенты a0 и a1 определяются из условия: сумма квадратов отклонений экспериментальных значений y от рассчитанных по уравнению регрессии должна быть минимальной.
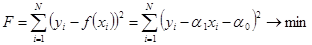
Для отыскания минимума составим систему уравнений
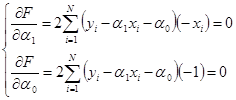
Решая эту систему, получаем значения коэффициентов:
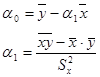
Обозначим через rxy оценку коэффициента линейной корреляции:
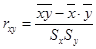 .
.
Тогда коэффициенты регрессии определяются равенствами
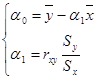
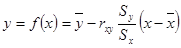 - уравнение линейной регрессии.
- уравнение линейной регрессии.
Аналогичные вычисления для второго уравнения регрессии x = b 1 y + b 0 = g ( y ) дают следующие значения коэффициентов:
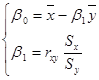 .
.
Тогда уравнение регрессии имеет вид:
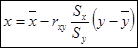 .
.
Свойства коэффициента линейной корреляции:
1.Коэффициент линейной корреляции rxy по абсолютной величине не превышает 1: 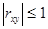
2.Если X и Y (случайные величины) независимы, то rxy =0, обратное утверждение верно не всегда.
3.Если rxy = ± 1, то величины X , Y связаны функциональной линейной зависимостью.
4.Если 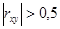 , то зависимость X и Y строят в виде линейной функции. В случае
, то зависимость X и Y строят в виде линейной функции. В случае 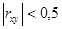 рассматриваются другие виды зависимости, например, квадратичная зависимость, гиперболическая, логарифмическая:
рассматриваются другие виды зависимости, например, квадратичная зависимость, гиперболическая, логарифмическая:
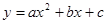 ,
, 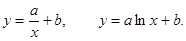
Дата: 2019-05-28, просмотров: 367.