Суть метода состоит в том, что специалистам (экспертам), хорошо знакомым с исследуемым процессом, предлагается расположить факторы в порядке убывания степени их влияния на переменную состояния.
Пусть приглашены m экспертов, которым предложено проранжировать n факторов: x1, x2,...,xn. Обозначим через а ij - ранг, выставляемый i-ым экспертом j-му фактору (1£а ij £n; i=1,...,m; j=1,...,n).
Результаты опроса заносятся в сводную таблицу:
Таблица 5.
| фактор | X 1 | X 2 | ................ | Xn |
| №спец | ||||
| 1 2 : : : m | a11 a21 : : : am1 | A12 a22 : : : am2 | ................ ................ ................ ................ ................ ................ | A1n a2n : : : amn |
Сумма рангов по строке (сумма рангов, выставляемых конкретным экспертом) для всех строк одинакова
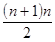 .
.
Среднее значение рангов в строке:
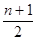
Среднее значение суммы рангов фиксированного фактора:
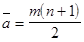
По результатам опроса экспертов проверяется гипотеза H 0: мнение экспертов согласованы, при альтернативной гипотезе H 1: мнения экспертов не согласованы. Вычисляется коэффициент согласия (коэффициент конкордации):
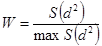 ,
,
где S ( d 2 ) - сумма квадратов отклонения суммы рангов от средней суммы:
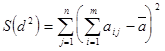 ,
,
а 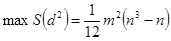 .
.
Если мнения экспертов согласованны, то:
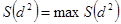
Если мнения экспертов рассогласованны, то: S ( d 2 ) близко к 0.
Таким образом, получаем, что если мнения экспертов согласованны, то коэффициент конкордации W = 1. Если мнения экспертов полностью рассогласованны, то W » 0.
Для проверки нулевой гипотезы в качестве статистического критерия выбираем случайную величину ( n -1) × m × W. Доказано, что при n >7 эта случайная величина имеет c 2.- распределение с числом степеней свободы f = n - 1. Таким образом, критическое значение критерия определяется по таблице критических точек c 2.-распределения в зависимости от q и f. Наблюдаемое значение:
c 2.набл.= ( n -1) × m × W
Если c 2.набл.> c 2.кр., то мнения экспертов согласуются. В противном случае мнения экспертов рассогласованны (критическая область левосторонняя).
Если из нескольких факторов эксперт ни одному не может отдать предпочтение, то в этом случае в таблицу ранжирования этим факторам он выставляет одинаковые дробные ранги . Коэффициент конкордации вычисляется по формуле:
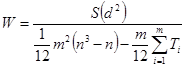 ,
,
где
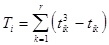 ,
,
где i - номер эксперта;
k - номер повторения;
tik - число одинаковых рангов в k-ом повторении.
Если мнения экспертов согласованны, то строится ранжировочная диаграмма. В ней по оси абсцисс откладываются факторы, по оси ординат - суммы рангов в обратном порядке. По виду диаграммы судят о значимом или незначимом влиянии факторов на переменную состояния и об использовании факторов в основном эксперименте.
Пример:
Для некоторого технологического объекта рассматриваются шесть факторов, влияющих на переменную состояния. Мнения четырёх экспертов приведены в таблице. Проверить гипотезу о согласованности экспертов и, если она справедлива, то изобразить гистограмму ранжирования.
Таблица 7.
| №ф./ №спец | x 1 | x 2 | X 3 | X 4 | x 5 | x 6 | ti1 | t3i1-ti1 | ti2 | t3i2- ti2 | Ti |
| 1 | 1.5 | 5 | 1.5 | 4 | 3 | 6 | 2 | 6 | 0 | 6 | |
| 2 | 2 | 3 | 1 | 4.5 | 4.5 | 6 | 2 | 6 | 0 | 6 | |
| 3 | 2 | 3 | 1 | 5.5 | 5.5 | 4 | 2 | 6 | 0 | 6 | |
| 4 | 1.5 | 3.5 | 1.5 | 5 | 3.5 | 6 | 2 | 6 | 2 | 6 | 12 |
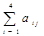
| 7 | 14.5 | 5 | 19 | 16.5 | 2.2 | |||||
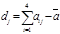
| -7 | 0.5 | -9 | 5 | 2.5 | 8 | |||||
| dj2 | 49 | 0.25 | 81 | 25 | 6.25 | 64 |
m=4; n=6.
Средняя сумма рангов в столбце:
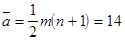 .
.
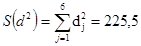 .
.
Вычислим коэффициент конкордации:
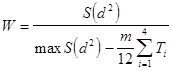
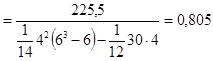 .
.
Наблюдаемое значение критерия определяется по формуле:
c 2.набл =m(n-1)W=4×5×0,805=16,1..
Критическое значение критерия находим в таблице для уровня значимости q=0.05 и числа степеней свободы f = n - 1 = 6 – 1 = 5:
c 2.кр.= c 2.(0,05;5)=11,07.
Так как c 2.набл.> c 2.кр., то мнения экспертов согласованны.
 åаij
åаij





 0
0







 10
10





 20
20


 30 X
30 X
X3 X1 X2 X5 X4 X6
Рис.2. Ранжировочная гистограмма.
Дата: 2019-05-28, просмотров: 279.