Перечень функций обработки данных, расположенных в директории MATLAB-а datafun приведен в Приложении 8 .
Рассмотрим гипотетический числовой пример, который основан на ежечасном подсчете чис-ла машин, проходящих через три различные пункта в течении 24 часов. Допустим, результа-ты наблюдений дают следующую матрицу count
count =
11 11 9
7 13 11
14 17 20
11 13 9
43 51 69
38 46 76
61 132 186
75 135 180
38 88 115
28 36 55
12 12 14
18 27 30
18 19 29
17 15 18
19 36 48
32 47 10
42 65 92
57 66 151
44 55 90
114 145 257
35 58 68
11 12 15
13 9 15
10 9 7
Таким образом, мы имеем 24 наблюдения трех переменных. Создадим вектор времени, t, со-стоящий из целых чисел от 1 до 24: t = 1 : 24. Построим теперь зависимости столбцов матри-цы counts от времени и надпишем график:
plot(t, count)
legend('Location 1','Location 2','Location 3',0)
xlabel('Time')
ylabel('Vehicle Count')
grid on
где функция plot(t, count) строит зависимости трех векторов-столбцов от времени; функция
legend('Location 1','Location 2','Location 3',0) показывает тип кривых; функции xlabel и ylabel надписывают координатные оси, а grid on выводит координатную сетку. Соответству-ющий график показан ниже.
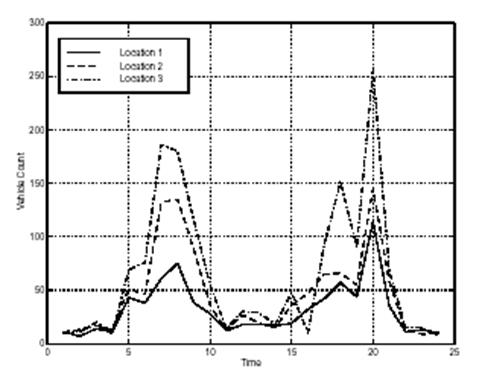
Применим к матрице count функции max (максимальное значение), mean (среднее значение) и std (стандартное, или среднеквадратическое отклонение).
mx = max(count)
mu = mean(count)
sigma = std( count)
В результате получим
mx =
114 145 257
mu =
32.00 46.5417 65.5833
sigma =
25.3703 41.4057 68.0281
где каждое число в строке ответов есть результат операции вдоль соответствующего столбца матрицы count. Для определения индекса максимального или минимального элемента нужно в соответствующей функции задать второй выходной параметр. Например, ввод
[mx,indx] = min(count)
mx =
7 9 7
indx =
2 23 24
показывает, что наименьшее число машин за час было зарегестрировано в 2 часа для первого пункта наблюдения (первый столбец) и в 23 и 24 чч. для остальных пунктов наблюдения.
Вы можете вычесть среднее значение из каждого столбца данных, используя внешнее произ-ведение вектора, составленного из единиц и вектора mu (вектора средних значений)
e = ones(24, 1)
x = count - e*mu
Перегруппировка данных может помочь вам в оценке всего набора данных. Так, использование в системе MATLAB в качестве единственного индекса матрицы двоеточия, приводит к представлению этой матрицы как одного длинного вектора, составленного из ее столбцов. Поэтому, для нахождения минимального значения всего множества данных можно ввести
Min(count(:))
что приводит к результату
ans =
7
Запись count(:) в данном случае привела к перегруппировке матрицы размера 24х3 в вектор-столбец размера 72х1.
Матрица ковариаций и коэффициенты корреляции
Для статистической обработки в MATLAB-е имеются две основные функции для вычисле-ния ковариации и коэффициентов корреляции:
· cov – В случае вектора данных эта функция выдает дисперсию, то есть меру распреде-
ления (отклонения) наблюдаемой переменной от ее среднего значения. В случае
матриц это также мера линейной зависимости между отдельными переменными,
определяемая недиагональными элементами.
· corrcoef – Коэффициенты корреляции – нормализованная мера линейной вероятност-ной зависимости между перменными.
Применим функцию cov к первому столбцу матрицы count
Cov(count(:,1))
Результатом будет дисперсия числа машин на первом пункте наблюдения
ans =
643.6522
Для массива данных, функция cov вычисляет матрицу ковариаций. Дисперсии столбцов мас-сива данных при этом расположены на главной диагонали матрицы ковариаций. Остальные элементы матрицы характеризуют ковариацию между столбцами исходного массива. Для матрицы размера mхn, матрица ковариаций имеет размер n-by-n и является симметричной, то есть совпадает с транспонированной.
Функция corrcoef вычисляет матрицу коэффициентов корреляции для массива данных, где каждая строка есть наблюдение, а каждый столбец – переменная. Коэффициент корреляции – это нормализованная мера линейной зависимости между двумя переменными. Для некор-релированных (линейно-независимых) данных коэффициент корреляции равен нулю; экива-лентные данные имеют единичный коэффициент корреляции. Для матрицы mхn, соответст-вующая матрица коэффициентов корреляции имеет размер nхn. Расположение элементов в матрице коэффициентов корреляции аналогично расположению элементов в рассмотренной выше матрице ковариаций. Для нашего примера подсчета количества машин, при вводе
Corrcoef( count)
получим
ans =
1.0000 0.9331 0.9599
0.9331 1.0000 0.9553
0.9599 0.9553 1.0000
Очевидно, здесь имеется сильная линейная корреляция между наблюдениями числа машин в трех различных точках, так как результаты довольно близки к единице.
Конечные разности
MATLAB предоставляет три функции для вычисления конечных разностей.
| Функция | Описание |
| diff | Разность между двумя последовательными элементами вектора. Приближенное дифференцирование. |
| gradient | Приближенное вычисление градиента функции. |
| del2 | Пятиточечная аппроксимация Лапласиана. |
Функция diff вычисляет разность между последовательными элементами числового вектора, то есть diff(X) есть [X(2) -X(1) X(3) -X(2) ... X(n) -X(n-1)]. Так, для вектора A,
A = [9 -2 3 0 1 5 4];
Diff(A)
MATLAB возвращает
ans =
-11 5 -3 1 4 -1
Помимо вычисления первой разности, функция diff является полезной для определения опре-деленных характеристик вектора. Например, вы можете использовать diff для определения, является ли вектор монотонным (значения элементов или всегда возрастают или убывают), или имеет ли он равные приращения и т.д. Следующая таблица описывает несколько различ-ных путей использования функции diff с одномерным вектором x.
| Применение (тест) | Описание |
| diff(x) == 0 | Тест на определение повторяющихся элементов |
| all(diff(x) > 0) | Тест на монотонность |
| all(diff(diff(x)) == 0) | Тест на опредедление равных приращений |
Обработка данных
В данном разделе рассматривается как поступать с:
· Отсутствующими значениями
· Выбросами значений или несовместимыми («неуместными») значениями
Отсутствующие значения
Специальное обозначение NaN, соответствует в MATLAB-е нечисловое значение. В соответ-ствие с принятыми соглашениями NaN является результатом неопределенных выражений та-ких как 0/0. Надлежащее обращение с отсутствующими данными является сложной пробле-мой и зачастую меняется в различных ситуациях. Для целей анализа данных, часто удобно использовать NaN для представления отсутствующих значений или данных которые недос-тупны. MATLAB обращается со значениями NaN единообразным и строгим образом. Эти значения сохраняются в процессе вычислений вплоть до конечных результатов. Любое мате-матическое действие, производимое над значением NaN, в результате также производит NaN. Например, рассмотрим матрицу, содержащую волшебный квадрат размера 3х3, где це-нтральный элемент установлен равным NaN.
a = magic(3); a(2,2) = NaN;
a =
8 1 6
NaN 7
4 9 2
Вычислим сумму элементов всех столбцов матрицы:
sum( a)
ans =
NaN 15
Любые математические действия над NaN распространяют NaN вплоть до конечного резуль-тата. Перед проведением любых статистических вычислений вам следует удалить все NaN-ы из имеющихся данных. Вот некоторые возможные пути выполнения данной операции.
| Программа | Описание |
| i = find( ~ isnan(x)); x = x(i) | Найти индексы всех эементов вектора, не равных NaN, и затем сохранить только эти элементы |
| x = x (find( ~ isnan(x))) | Удалить все NaN-ы из вектора |
| x = x ( ~ isnan(x)); | Удалить все NaN-ы из вектора (быстрее). |
| x (isnan(x)) = [ ]; | Удалить все NaN-ы из вектора |
| X (any(isnan(X’)), :) = [ ]; | Удалить все строки матрицы X содержащие NaN-ы |
Внимание. Для нахождения нечисловых значений NaN вам следует использовать специаль-ную функцию isnan, поскольку при принятом в MATLAB-е соглашении, логическое сравне-ние NaN == NaN всегда выдает 0. Вы не можете использовать запись x(x==NaN) = [ ] для удаления NaN-ов из ваших данных.
Если вам часто приходится удалять NaN-ы, воспользуйтесь короткой программой, записан-ной в виде М-файла.
function X = excise(X)
X(any(isnan(X')),:) = [ ];
Тогда. напечатав
X = excise(X);
вы выполните требуемое действие (excise по английски означает вырезать)
Удаление выбросов значений
Вы можете удалить выбросы значений или несовместимые данные при помощи процедур, весьма схожих с удалением NaN-ов. Для нашей транспортной задачи, с матрицей данных count, средние значения и стандартные (среднеквадратические) отклонения каждого столбца матрицы count равны
mu = mean(count)
sigma = std(count)
mu =
32.0000 46.5417 65.5833
sigma =
25.3703 41.4057 68.0281
Число строк с выбросами значений, превышающими утроенное среднеквадратическое откло-нение от среднего значения можно получить следующим образом:
[n, p] = size(count)
outliers = abs(count - mu(ones(n, 1),:)) > 3*sigma(ones(n, 1),:);
nout = sum( outliers)
nout =
1 0 0
Имеется только один выброс в первом столбце. Удалим все наблюдение при помощи выра-жения
count( any( outliers'),:) = [ ];
Регрессия и подгонка кривых
Часто бывает полезным или необходимым найти функцию, которая описывает взаимосвязь между некоторыми наблюдаемыми (или найденными экспериментально) переменными. Оп-ределение коэффициентов такой функции ведет к решению задачи переопределенной систе-мы линейных уравнений, то есть системы, у которой число уравнений превышает число не-известных. Указанные коэффициенты можно легко найти с использованием оператора обрат-ного деления \ (backslash). Допустим, вы производили измерения переменной y при разных значениях времени t.
t = [0 0.3 0.8 1.1 1.6 2.3]';
y = [0.5 0.82 1.14 1.25 1.35 1.40]';
Plot(t,y,'o'); grid on
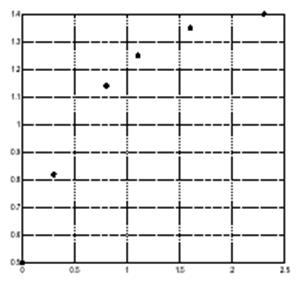
В следующих разделах мы рассмотрим три способа моделирования (аппроксимации) этих данных:
· Методом полиномиальной регрессии
· Методом линейно-параметрической (linear-in-the-parameters) регрессии
· Методом множественной регрессии
Полиномиальная регрессия
Основываясь на виде графика, можно допустить, что данные могут быть аппроксимированы полиномиальной функцией второго порядка:
y = a 0 + a 1 t + a 2 t 2
Неизвестные коэффициенты a0 , a1 и a2 могут быть найдены методом среднеквадратичес-кой подгонки (аппроксимации), которая основана на минимизации суммы квадратов отклоне-ний данных от модели. Мы имеем шесть уравнений относительно трех неизвестных,
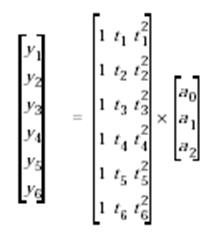
представляемых следующей матрицей 6х3:
X = [ ones( size( t)) t t.^2]
X = 1.0000 0 0
1.0000 0.3000 0.0900
1.0000 0.8000 0.6400
1.0000 1.1000 1.2100
1.0000 1.6000 2.5600
1.0000 2.3000 5.2900
Решение находится при помощи оператора \ :
a = X\ y
a =
0.5318
0.9191
- 0.2387
Следовательно, полиномиальная модель второго порядка наших данных будет иметь вид
y = 0.5318 + 0.9191 t – 0.2387 t2
Оценим теперь значения модели на равноотстоящих точках (с шагом 0.1) и нанесем кривую на график с исходными данными.
T = (0 : 0.1 : 2.5)';
Y = [ones(size(T)) T T.^2]*a;
Plot(T,Y,'-',t,y,'o'); grid on
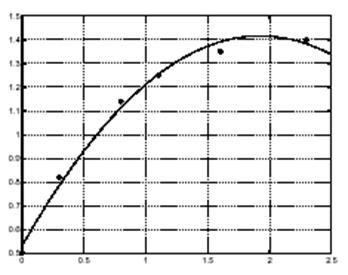
Очевидно, полиномиальная аппроксимация оказалась не столь удачной. Здесь можно или по-высить порядок аппроксимирующего полинома, или попытаться найти какую-либо другую функциональную зависимость для получения лучшей подгонки.
Линейно-параметрическая регрессия[1]
Вместо полиномиальной функции, можно было-бы попробовать так называемую линейно-параметрическую функцию. В данном случае, рассмотрим экспоненциальную функцию
y = a 0 + a 1 ℮- t + a 2 t ℮- t
Здесь также, неизвестные коэффициенты a0 , a1 и a2 могут быть найдены методом наимень-ших квадратов. Составим и решим систему совместных уравнений, сформировав регресси-онную матрицу X, и применив для определения коэффициентов оператор \ :
X = [ones(size(t)) exp(- t) t.*exp(- t)];
a = X\ y
a =
1.3974
- 0.8988
0.4097
Значит, наша модель данных имеет вид
y = 1.3974 – 0.8988 ℮- t + 0.4097 t ℮- t
Оценим теперь, как и раньше, значения модели на равноотстоящих точках (с шагом 0.1) и на-несем эту кривую на график с исходными данными.
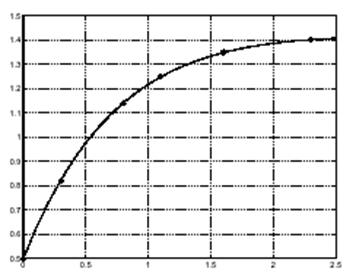
Как видно из данного графика, подгонка здесь намного лучше чем в случае полиномиальной функции второго порядка.
Множественная регрессия
Рассмотренные выше методы аппроксимации данных можно распространить и на случай бо-лее чем одной независимой переменной, за счет перехода к расширенной форме записи. До-пустим, мы измерили величину y для некоторых значений двух параметров x 1 и x 2 и полу-чили следующие результаты
x1 = [0.2 0.5 0.6 0.8 1.0 1.1]' ;
x2 = [0.1 0.3 0.4 0.9 1.1 1.4]' ;
y = [0.17 0.26 0.28 0.23 0.27 0.24]' ;
Множественную модель данных будем искать в виде
y = a 0 + a 1 x 1 + a 2 x 2
Методы множественной регрессии решают задачу определения неизвестных коэффициентов a0 , a1 и a2 путем минимизации среднеквадратической ошибки приближения. Составим сов-местную систему уравнений, сформировав матрицу регрессии X и решив уравнения отно-сительно неизвестных коэффициентов, применяя оператор \ .
X = [ones(size(x1)) x1 x2];
a = X\ y
a =
0.1018
0.4844
-0.2847
Следовательно, модель дающая минимальную среднеквадратическую ошибку аппроксима-ции имеет вид
y = 0.1018 + 0.4844x1 – 0.2847x2
Для проверки точности подгонки найдем максимальное значение абсолютного значения от-клонений экспериментальных и расчетных данных.
Y = X*a;
MaxErr = max(abs(Y - y))
MaxErr =
0.0038
Эта ошибка дает основание утверждать, что наша модель достаточно адекватно отражает ре-зультаты наблюдений.
Дата: 2019-05-28, просмотров: 307.