Если матрица А является квадратной и невырожденной, уравнения AX = I и XA = I имеют одинаковое решение X. Это решение называется матрицей обратной к A, обозначается через A-1 и вычисляется при помощи функции inv. Понятие детерминанта (определителя) матрицы полезно при теоретических выкладках и некоторых типах символьных вычислений, но его масштабирование и неизбежные ошибки округления делают его не столь привлекательным при числовых вычислениях. Тем не менее, если это требуется, функция det вычисляет определитель квадратной матрицы. Например,
A = pascal (3)
A =
1 1 1
1 2 3
1 3 6
d = det (A)
X = inv (A)
d =
1
X =
3 -3 1
-3 5 -2
1 -2 1
Опять таки, поскольку A является симметричной матрицей целых чисел и имеет единичный определитель, то же самое справедливо и для обратной матрицы. С другой стороны, для
B = magic(3)
B =
8 1 6
3 5 7
4 9 2
d = det( B)
X = inv( B)
d =
-360
X =
0.1472 -0.1444 0.0639
-0.0611 0.0222 0.1056
-0.0194 0.1889 -0.1028
Внимательное изучение элементов матрицы X, или использование формата rational , показы-вает, что они являются целыми числами, разделенными на 360.
Если матрица A является квадратной и несингулярной, то, пренебрегая ошибками округле-ния, выражение X = inv(A)*B теоретически означает то же, что и X = A\B , а Y = B*inv(A) теоретически есть то же, что и Y = B/A. Однако вычисления включающие операторы \ и / более предпочтительны, поскольку требуют меньше рабочего времени, меньшей памяти и имеют лучшие свойства с точки зрения определения ошибок.
Псевдообратные матрицы
Прямоугольные матрицы не имеют детерминантов и обратных матриц. Для таких матриц по крайней мере одно из уравнений AX = I или XA = I не имеет решения. Частично данный про-бел восполняется так называемой псевдообратной матрицей Мура-Пенроуза, или просто псевдообратной матрицей, которая вычисляется при помощи функции pinv. На практике необходимость в этой операции встречается довольно редко. Желающие могут всегда обра-титься к соответствующим справочным пособиям.
Степени матриц и матричные экспоненты
Положительные целые степени
Если А есть некоторая квадратная матрица, а р – положительное целое число, то A^p эквива-лентно умножению A на себя р раз.
X = A^2
X =
3 6 10
6 14 25
10 25 46
Отрицательные и дробные степени
Если А является квадратной и невырожденной, то A^(-p) эквивалентно умножению inv(A) на себя p раз.
Y = B^(-3)
Y =
0.0053 -0.0068 0.0018
-0.0034 0.0001 0.0036
-0.0016 0.0070 -0.0051
Дробные степени, например A^(2/3), также допускаются; результаты при этом зависят от ра-спределения собственных значений матрицы А.
Поэлементное возведение в степень
Оператор .^ (с точкой !) осуществляет поэлементное возведение в степень. Например,
X = A.^2
A =
1 1 1
1 4 9
1 9 36
Вычисление корня квадратного из матрицы и матричной экспоненты
Для невырожденных квадратных матриц А функция sqrtm вычисляет главное значение квад-ратного корня , т.е. если X = sqrtm(A) , то X*X = A . Буква m в sqrtm означает, что выпол-няется матричная операция. Это отличает данную функцию от sqrt(A), которая, подобно A.^(1/2) (обратите внимание на точку !), выполняет операцию извленчения корня поэлемен-тно.
Система обыкновенных линейных дифференциальных уравнений первого порядка может быть записана в виде
dx/dt = Ax
где x = x(t) есть векторная функция от t, а A есть постоянная матрица не зависящая от t.
Решение данной системы может быть выражено в виде матричной экспоненты.
x( t) = ℮ At x(0)
Функция expm(A) вычисляет матричную экспоненту. Рассмотрим пример системы диффере-нциальных уравнений со следующей 3х3 матрицей коэффициентов
A =
0 -6 -1
6 2 -16
-5 20 -10
и начальными условиями x(0)
x0 = [ 1 1 1]’.
Использование матричной экспоненты для вычисления решения дифференциального уравне-ния в 101 точке с шагом 0.01 на интервале 0 ≤ t ≤ 1 записывается в виде
X = [ ];
for t = 0 : 0.01 : 1
X = [ X expm( t* A)* x0];
end
Трехмерный график решения в фазовом пространстве может быть получен при помощи спе-циальной функции
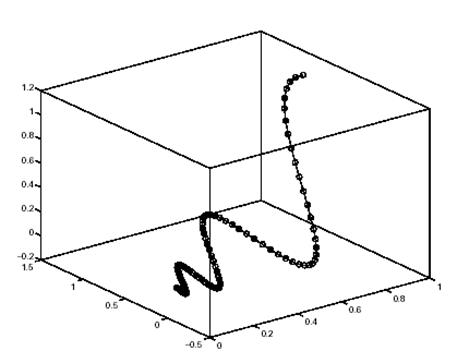
Plot3(X(1,:), X(2,:), X(3,:), '-o')
Решение имеет вид спиральной функции сходящейся к началу координат (см. рис. ниже). Та-кое решение обусловлено комплексными собственными значениями матрицы коэффициен-тов А.
Дата: 2019-05-28, просмотров: 339.