Функция polyval вычисляет значение полинома в заданных точках. Для вычисления p в точ-ке s = 5, следует записать
Polyval( p,5)
ans =
110
Можно также вычислить значение матричного полинома. Так, вместо полинома Валлиса мо-жно записать:
p( X) = X3 - 2 X – 5 I
где X является квадратной матрицей, а I - единичной матрицей. Например, сформируем сле-дующую квадратную матрицу X
X = [2 4 5; -1 0 3; 7 1 5];
и вычислим значение заданного выше полинома p(X) на данной матрице.
Y = polyvalm(p, X)
Y =
377 179 439
111 81 136
490 253 639
Умножение и деление полиномов
Для умножения и деления полиномов предназначены соответственно функции conv и deconv. Рассмотрим полиномы a(s) = s2 + 2s + 3 и b(s) = 4s2 + 5s + 6. Для вычисления их произведения следует ввести
a = [1 2 3]; b = [4 5 6];
c = conv( a, b)
MATLAB возвращает
c =
4 13 28 27 18
Для получения из с полинома b воспользуемся функцией deconv:
[q, r] = deconv(c, a)
q =
4 5 6
r =
0 0 0 0 0
где r – остаток после деления (в данном случае нулевой вектор). В общем случае для поли-номов q, r , c, a в функции deconv справедливо соотношение
c = conv( q, a) + r
Вычисление производных от полиномов
Функция polyder вычисляет производную любого полинома. Для получения производной от нашего полинома p = [1 0 -2 -5], введем
q = polyder( p)
q =
3 0 - 2
Функция polyder вычисляет также производные от произведения или частного двух полино-мов. Например, создадим два полинома a и b:
a = [1 3 5]; b = [2 4 6];
Вычислим производную произведения a*b вводом функции polyder с двумя входными аргу-ментами a и b и одним выходным:
c = polyder(a, b)
c =
8 30 56 38
Вычислим производную от частного a/b путем ввода функции polyder с двумя выходными аргументами:
[q, d] = polyder(a, b)
q =
-2 -8 -2
d =
4 16 40 48 36
где отношение двух полиномов q/d является результатом операции дифференцирования.
Аппроксимация кривых полиномами
Функция polyfit находит коэффициенты полинома заданной степени n , который аппрокси-мирует данные (или функцию y(x)) в смысле метода наименьших квадратов:
p = polyfit(x, y, n)
где x и y есть векторы, содержащие данные x и y, которые нужно аппроксимировать полино-мом. Например, рассмотрим совокупность данных x-y, полученную экспериментальным пу-тем
x = [1 2 3 4 5]; y = [5.5 43.1 128 290.7 498.4].
Аппроксимация функциональной зависимости y(x) в виде полинома третьего порядка
p = polyfit( x, y,3)
дает коэффициенты полинома
p =
-0.1917 31.5821 -60.3262 35.3400
Рассчитаем теперь значения полинома, полученного при помощи функции polyfit, на более мелкой шкале (с шагом 0.1) и построим для сравнения графики (это делает функция plot) реальных данных и аппроксимирующей кривой.
x2 = 1 : 0.1 : 5;
y2 = polyval(p, x2);
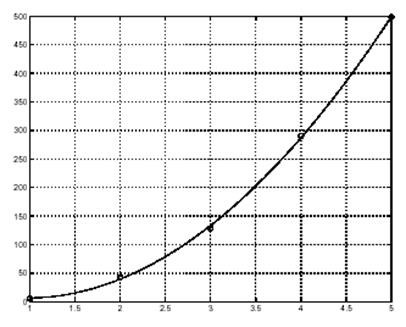
Plot(x, y, 'o', x2, y2); grid on
где функция grid on служит для нанесения координатной сетки, а экспериментальные дан-ные на графике отмечены маркерами о.
 .
.
Как видно из рисунка, полином третьего порядка достаточно хорошо аппроксимирует наши данные.
Разложение на простые дроби
Функция residue вычисляет вычеты, полюса и многочлен целой части отношения двух поли-номов. Это особенно полезно при представлении систем управления в виде передаточных функций. Для полиномов a(s) и b(s), при отсутствии кратных корней имеем
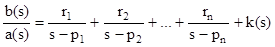
где r есть вектор-столбец вычетов, p есть вектор-столбец полюсов, а k есть вектор-строка це-лой части дробно-рациональной функции. Рассмотрим передаточную функцию

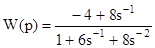
Для полиномов числителя и знаменателя этой функции имеем:
b = [-4 8]; a = [1 6 8].
Введя
[r, p, k] = residue(b, a)
получим
r =
-12
8
p =
-4
-2
k =
[ ]
Функция residue с тремя входными (r, p, и k) и двумя выходными (b2, a2) аргументами вы-полняет обратную функцию свертки имеющегося разложения на простые дроби, в дробно-рациональную функцию отношения двух полиномов.
[b2, a2] = residue(r, p, k)
b2 =
-4 8
a2 =
1 6 8
т.е. из данных предыдущего примера мы восстановили исходную передаточную функцию.
В случае кратных корней процедура несколько усложняется, но остается разрешимой.
Интерполяция
Интерполяция является процессом вычисления (оценки) промежуточных значений функций, которые находятся между известными или заданными точками. Она имеет важное приме-нение в таких областях как теория сигналов, обработка изображений и других. MATLAB обеспечивает ряд интерполяционных методик, которые позволяют находить компромисс ме-жду точностью представления интерполируемых данных и скоростью вычислений и исполь-зуемой памятью.
Обзор функций интерполяции
Одномерная интерполяция
Двумя основными типами одномерной интерполяции в MATLAB-е являются полиномиаль-ная интерполяция и интерполяция на основе быстрого преобразования Фурье.
Полиномиальная интерполяция
Функция interp1 осуществляет одномерную интерполяцию – важную операцию в области анализа данных и аппроксимации кривых. Эта функция использует полиномиальные методы, аппроксимируя имеющийся массив данных полиномиальными функциями и вычисляя соот-ветствующие функции на заданных (желаемых) точках. В наиболее общей форме эта функ-ция имеет вид
yi = interp1( x, y, xi, method)
где y есть вектор, содержащий значения функции; x – вектор такой же длины, содержащий те точки (значения аргумента), в которых заданы значения y; вектор xi содержит те точки, в ко-торых мы хотим найти значения вектора y путем интерполяции; method – дополнительная строка, задающая метод интерполяции. Имеются следующие возможности для выбора мето-да:
• Ступенчатая интерполяция (method = 'nearest'). Этот метод приравнивает значение функ-ции в интерполируемой точке к ее значению в ближайшей существующей точке имеющихся данных.
• Линейная интерполяция (method = 'linear'). Этот метод аппроксимирует функцию между любыми двумя существующими соседними значениями как линейную функцию, и возвр-ащает соответствующее значение для точки в xi (метод используется по умолчанию).
• Интерполяция кубическими сплайнами (method = 'spline'). Этот метод аппроксимирует ин-терполируемую функцию между любыми двумя соседними значениями при помощи куби-ческих функций, и использует сплайны для осуществления интерполяции.
• Кубическая интерполяция (method = 'pchip' или 'cubic'). Эти методы идентичны. Они ис-пользуют кусочную кубическую Эрмитову аппроксимацию и сохраняют монотонность и форму данных.
Если какой-либо из элементов вектора xi находится вне интервала, заданного вектором x, то выбранный метод интерполяции используется также и для экстраполяции. Как альтернатива,
функция yi = interp1(x, y, xi, method, extrapval) заменяет экстраполированные значения теми, которые заданы вектором extrapval. Для последнего часто используется нечисловое значение NaN.
Все методы работают на неравномерной сетке значений вектора x .
Рассмотрение скорости, требуемой памяти и гладкости методов. При выборе метода ин-терполяции всегда нужно помнить, что некоторые из них требуют большего объема памяти или выполняются быстрее, чем другие. Однако, вам может потребоваться использование лю-бого из этих методов, чтобы достичь нужной степени точности интерполяции (гладкости результатов). При этом нужно исходить из следующих критериев.
• Метод ступенчатой аппроксимации является самым быстрым, однако он дает наихудшие результаты с точки зрения гладкости.
• Линейная интерполяция использует больше памяти чем ступенчатая и требует несколько большего времени исполнения. В отличие от ступенчатой аппроксимации, результирующая функция является непрерывной, но ее наклон меняется в значениях исходной сетки (исход-ных данных).
• Кубическая интерполяция сплайнами требует наибольшего времени исполнения, хотя тре-бует меньших объемов памяти чем кубическая интерполяция. Она дает самый гладкий ре-зультат из всех других методов, однако вы можете получить неожиданные результаты, если входные данные распределены неравномерно и некоторые точки слишком близки.
• Кубическая интерполяция требует большей памяти и времени исполнения чем ступенчатая или линейная. Однако в данном случае как интерполируемые данные, так и их производные являются непрерывными.
Относительные качественные характеристики всех перечисленных методов сохраняются и в случае двух- или многомерной интерполяции.
2. Интерполяция на основе быстрого преобразования Фурье _
Функция interpft осуществляет одномерную интерполяцию с использованием быстрого пре-образование Фурье (FFT). Этот метод вычисляет преобразование Фурье от вектора, который содержит значения периодической функции. Затем вычисляется обратное преобразование Фурье с использованием большего числа точек. Функция записывается в форме
y = interpft( x, n)
где x есть вектор, содержащий дискретные значения периодической функции, заданной на равномерной сетке, а n - число равномерно распределенных точек, в которых нужно оценить значения интерполируемой функции.
Двумерная интерполяция
Функция interp2 осуществляет двумерную интерполяцию - важную операцию при обработке изображений и графического представления данных. В наиболее общей форме эта команда имеет вид
ZI = interp2( X, Y, Z, XI, YI, method)
где Z есть прямоугольный массив, содержащий значения двумерной функции; X и Y являют-ся массивами одинаковых размеров, содержащие точки в которых заданы значения двумер-ной функции; XI и YI есть матрицы, содержащие точки интерполяции (то есть промежуточ-ные точки, в которых нужно вычислить значения функции); method – строка, определяющая метод интерполяции. В случае двумерной интерполяции возможны три различных метода:
• Ступенчатая интерполяция (method = 'nearest'). Этот метод дает кусочно-постоянную поверхность на области значений. Значение функции в интерполируемой точке равно значе-нию функции в ближайшей заданной точке.
• Билинейная интерполяция (method = 'linear'). Метод обеспечивает аппроксимацию данных при помощи билинейной поверхности (плоскости) на множестве заданных значений двумер-ной функции. Значение в точке интерполяции является комбинацией значений четырех бли-жайших точек. Данный метод можно считать «кусочно-билинейным»; он быстрее и требует меньше памяти, чем бикубическая интерполяция.
• Бикубическая интерполяция (method = 'cubic'). Данный метод аппроксимирует поверх-ность при помощи бикубических поверхностей. Значение в точке интерполяции является комбинацией значений в шестнадцати ближайших точках. Метод обеспечивает значительно более гладкую поверхность по сравнению с билинейной интерполяцией. Это может быть ключевым преимуществом в приложениях типа обработки изображений. Особенно эффек-тивным данный метод является в ситуациях, когда требуется непрерывность как интерполи-руемых данных, так и их производных.
Все эти методы требуют, чтобы X и Y были монотонными, то есть или всегда возрастающи-ми или всегда убывающими от точки к точке. Эти матрицы следует сформировать с исполь-зованием функции meshgrid, или же, в противном случае, нужно убедиться, что «схема» то-чек имитирует сетку, полученную функцией meshgrid. Перед интерполяцией, каждый из указанных методов автоматически отображает входные данные в равномерно распреде-ленную сетку. Если X и Y уже распределены равномерно, вы можете ускорить вычисления добавляя звездочку к строке метода, например, '*cubic'.
Дата: 2019-05-28, просмотров: 361.