В узле сопряжения стенки резервуара с. днищем возникают изгибающий момент Мо и поперечная сила Qo, которые распространяются вдоль образующей и относительно быстро затухают. Поскольку из-за небольшой жесткости днища соединение нельзя считать жестким защемлением, принято считать нижний край стенки упруго защемленным в днище. Следовательно, в заполненном резервуаре происходят деформации как стенки, так и днища, а так как сопряжение их неразъемно, то сумма деформаций стенки и днища в узле должна быть равна нулю. Для отыскания неизвестных Мо и Qo принято использовать один из методов строительной механики решения статически неопределимых стержневых систем. В самом деле, мысленно вырезав полоску единичной ширины из стенки резервуара и днища, благодаря симметричности нагрузки можем считать их системой из двух соединенных стержней. Расчетная схема узла сопряжения приведена на рис.77.
Для определения неизвестных напишем канонические уравнения метода сил, представляющие собой по сути уравнения неразрывности деформаций в узле:
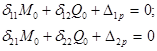 (3)
(3)
где 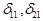 —единичные перемещения от действия;
—единичные перемещения от действия;
Мо = 1;
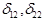 - единичные перемещения от действия Qo = 1l;
- единичные перемещения от действия Qo = 1l;
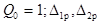 - перемещения от действия внешней нагрузки.
- перемещения от действия внешней нагрузки.
Каждое перемещение слагается из перемещений стенки и перемещения днища, т. е.
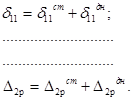
Днище в горизонтальном направлении (в своей плоскости) обладает значительной жесткостью, т. е. практически нерастяжимо, в чем нетрудно убедиться на опыте (с любым эластичным материалом, стараясь растянуть его равномерно во все стороны). Поэтому часть перемещений - коэффициентов системы канонических уравнений пропадает:
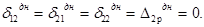
Поэтому система (3) принимает вид:
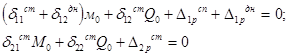 (4)
(4)
В дальнейшем решении задача сводится к отысканию единичных перемещений, являющихся коэффициентами системы уравнений (4), и решению последней.
Определение перемещений стенки
Для определения перемещений стенки напишем решение левой части дифференциального уравнения (решение однородного уравнения):
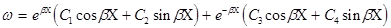 .
.
Поскольку стенка резервуара находится под действием гидростатического давления, изменяющегося по закону треугольника, то естественно предположить, что на бесконечном удалении от днища перемещения стенки должны быть равны нулю. Второе слагаемое приводимого решения действительно при 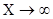 и стремится к нулю благодаря отрицательной степени при е. Первое же слагаемое может стать нулем только в том случае, если нулю равны произвольные постоянные C 1 и C 2. Таким образом, окончательно получаем:
и стремится к нулю благодаря отрицательной степени при е. Первое же слагаемое может стать нулем только в том случае, если нулю равны произвольные постоянные C 1 и C 2. Таким образом, окончательно получаем:
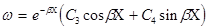 .
.
или для простоты вычислений
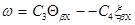 (5)
(5)
Выразим неизвестные произвольные постоянные
С3 С4 через неизвестные, но вполне определенные Мо и Qo (этот способ носит название метода начальных параметров). Для этого примем следующие граничные условия:
при х = 0
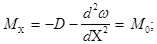
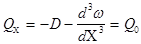 (6)
(6)
Взяв от выражения (5) вторую и третью производные (с помощью гиперболо-тригонометрических функций это сделать нетрудно) и подставив в них граничные условия (6), получим:
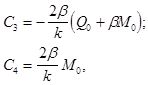
где k - величина, аналогичная коэффициенту постели в балках на упругого основании,
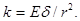
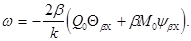 (7)
(7)
Уравнение углов поворота
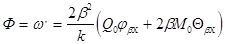 (8)
(8)
Уравнение изгибающих моментов
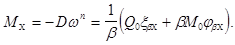 (9)
(9)
Уравнение поперечных сил
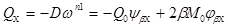 (10)
(10)
После отыскания М0 и Q0 по этим уравнениям можно построить эпюры перемещения, моментов и поперечных сил.
Перейдем непосредственно к отысканию перемещений. По существующему в методе сил правилу знаков 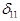 и
и 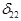 являются главными перемещениями, и если их направление совпадает с направлением действия силы (момента), то они имеют знак «плюс». Поэтому в уравнении (7) знак «минус» можно опустить.
являются главными перемещениями, и если их направление совпадает с направлением действия силы (момента), то они имеют знак «плюс». Поэтому в уравнении (7) знак «минус» можно опустить.
Для определения 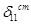 введем в уравнение (20) х = 0, Q о = 0 и М0 = 1, тогда получим:
введем в уравнение (20) х = 0, Q о = 0 и М0 = 1, тогда получим:
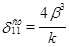
или
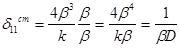
так как
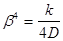 .
.
Подставив в уравнение (8) х = 0, М0 = 0 и Qo = l, получим:
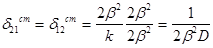 .
.
Такой же результат можно получить из уравнения (7), подставив в него х = 0, Qo = 0, Mo = 1 (по теореме о взаимности перемещений 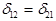 ).
).
Подставим в уравнение (7) х = 0, Мо = 0, Qo = 1, получим:
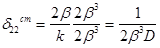 .
.
Для определения грузовых членов 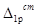 и
и 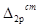 найдем частное решение для правой части уравнения
найдем частное решение для правой части уравнения
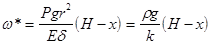 .
.
Тогда при х = 0
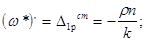
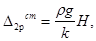
где Н—высота стенки резервуара.
Таким образом, определены все необходимые перемещения стенки.
6.4.3.1 Определение перемещений днища, лежащего на песчаной подушке. Для определения перемещений днища мысленно вырежем из него полоску единичной ширины в радиальном направлении. Будем рассматривать эту полоску как полубесконечную балку на упругом основании, нагруженную на расстоянии с от конца сосредоточенной силой (нагрузка от веса стенки и покрытия), сосредоточенным моментом М0 и равномерно распределенной нагрузкой р, т. е. гидростатическим давлением (рис. 76). Чтобы решить эту задачу, необходимо отдельно для каждого вида нагрузки составить решение для полубесконечной балки и фиктивной бесконечной балки на упругом основании, наложив эти решения для точки А (на расстоянии с от места приложения нагрузки) друг на друга, получить уравнения прогибов, углов поворота, сечений, моментов и поперечных сил для рассматриваемой балки-полоски.
Перемещение балки-полоски днища от действия изгибающего момента М0, передаваемого стенкой, будет:
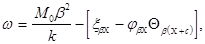 (11)
(11)
где р—коэффициент деформации днища,
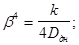
(k—коэффициент постели песчаного основания; k = 5?15 кг/см3);
D дн - цилиндрическая жесткость днища
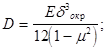
 -толщина окрайков днища;
-толщина окрайков днища; 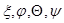 - гиперболо-тригонометрические функции. Угол поворота сечения
- гиперболо-тригонометрические функции. Угол поворота сечения
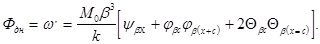 (12)
(12)
Изгибающий момент
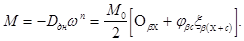 (13)
(13)
Единичное перемещение днища при х=0 (справа) получим» подставив Мо = 1 в уравнение (12):
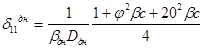
Величина изгибающего момента:
справа
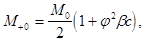
слева
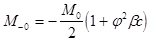
Перемещения днища от действия внешней нагрузки складываются из двух перемещений:
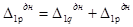
где 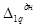 - перемещения от сосредоточенной силы q;
- перемещения от сосредоточенной силы q;
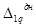 - перемещения от равномерно распределенной нагрузки р.
- перемещения от равномерно распределенной нагрузки р.
Перемещения от 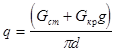 составляют
составляют
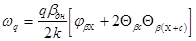 (14)
(14)
где G ст и Скр- массы соответственно стенки и крыши. Углы поворота сечений
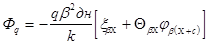 (15)
(15)
Изгибающие моменты
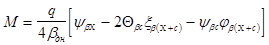 (16)
(16)
Подставив x = 0 в уравнение (15), получим
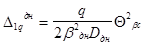
Знак «минус» опускаем, так как направление перемещения (поворота) 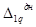 совпадает с направлением действия момента от силы q.
совпадает с направлением действия момента от силы q.
Перемещения от действия гидростатического давления P = p ∙ g ∙ H
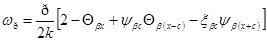 (17)
(17)
Угол поворота сечений
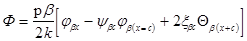 (18)
(18)
Изгибающий момент в днище
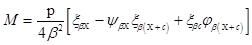 (19)
(19)
Подставив x = 0 в уравнение (18), получим:
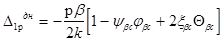
Знак «минус» в этом случае сохраняется, так как направление перемещения противоположно направлению действия нагрузки.
Подставив найденные значения перемещений в канонические уравнения (4), можно определить искомые величины М0 и Q 0. Значение поперечной силы Q0 обычно невелико (12—13% от абсолютной величины значения М0), поэтому влиянием ее на напряженное состояние узла сопряжения стенки с днищем можно пренебречь.
Эпюры изменения изгибающего момента и поперечных сил в стенке резервуара представлены на рис. Следует отметить, что явление подобное краевому эффекту у днища, имеется в зоне каждого кольцевого шва, соединяющего пояса резервуара. Однако благодаря незначительному различию толщины поясов и малой ширине самого шва влиянием этого явления можно пренебречь. Дополнительные напряжения в этих случаях по величине не превышают 5—7% значений кольцевого напряжения.
Для построения эпюр перемещений и изгибающих моментов, в стенке применяются уравнения (7), (8) и (9).
6.4.3.2 Расчет узла сопряжения при опирании резервуара на бетонное кольцо. Методика расчета узла сопряжения стенки с днищем при опирании резервуара на бетонное кольцо аналогична расчету узла резервуара, стоящего на песчаной подушке. Исключение в этом случае составляет порядок определения перемещений днища. Поскольку толщина бетонного кольца в 20—25 раз больше толщины окраек днища, трудно было бы ожидать, что кольцо будет работать, как упругое основание. Несмотря на то что модуль упругости (условный) бетона на целый порядок ниже модуля упругости стали, все же жесткость кольца больше жесткости окрайков. Осадку основания под кольцом можно не учитывать, так как после испытаний и первых заполнений его положение стабилизируется.
В расчетной схеме разбиваем (мысленно) днище на систему радиальных балок - полосок единичной ширины, но в отличие от предыдущего случая считаем каждую балку-полоску как балку на двух опорах (рис. 78,а), учитывая возможный отрыв участка днища от кольца. Балка находится под действием момента Мо, передаваемого от стенки и равномерно распределенного давления р (рис. 78,6). Нагрузку от веса стенки и покрытия здесь не учитываем, так как она вызывает только появление дополнительной реакции кольца, не влияющей на изгиб днища. Задача расчета балки по принятой схеме является нелинейной, потому что неизвестна величина пролета l (длина участка отрыва днища от кольца). Длина зависит от величины прилагаемых нагрузок. Так, с увеличением р длина l уменьшается, а с увеличением Мо возрастает. Для определения значения длины балки l введено дополнительное условие: положим, что на левом конце (см. рис. 78, б) опора В расположена там, где днище снова плотно прилегает к бетонному кольцу. Таким образом, можно считать, что на опоре В угол поворота сечения равен нулю.
Углы поворота сечений (угловые перемещения) на опорах можно определить любым способом по сопротивлению материалов (графоаналитический метод, способ Верещагина и др.).
Угол поворота сечения:
на опоре A 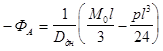 (20)
(20)
на опоре В 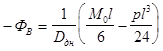 (21)
(21)
где D дн - цилиндрическая жесткость окрайков при изгибе.
По принятому ранее условию для опоры В Фв = 0.
Тогда из уравнения (21), приравнивая его 0, получим:
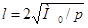
Подставив это значение l в уравнение (20), получим:
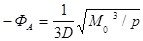
Так как направление перемещения совпадает с направлением момента Мо, знак «минус» опускаем. Окончательно имеем:
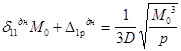 (22)
(22)
Из уравнения (22) следует, что из-за нелинейности задачи определить отдельно перемещения 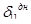 и
и 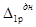 невозможно.
невозможно.
Подставив значение (22) в систему канонических уравнений (4) и решив их в общем виде, получим окончательное уравнение:
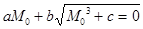 (23)
(23)
где
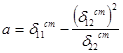 ;
;
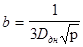 ;
;
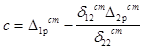
Уравнение (23) можно решить методом подбора значения Мо с помощью таблиц квадратов и кубов чисел или на ЭВМ. В обоих случаях полезно знать пределы изменения Мо. Нижнее значение определяется как М0 = 0 (шарнирное закрепление), а верхнее значение - из условия абсолютного жесткого защемления:
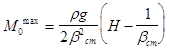 .
.
Расчет плавающей крыши
Для создания плавучести плавающей крыши прежде всего необходимо определить объем погруженной части понтонного кольца крыши, обеспечивающий достаточную для плавания выталкивающую силу. Условие плавания крыши можно записать так:
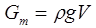
где G - масса крыши;
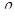 - плотность жидкости;
- плотность жидкости;
V - объем погруженной части понтонного кольца.
Расчет плавучести производят на воду и на нефтепродукт, т. е. в расчет вводят плотность воды 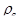 и плотность нефти или нефтепродукта
и плотность нефти или нефтепродукта 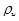 .
.
Распределенную нагрузку q, действующую на крыша, можно определить по формуле
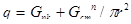
где G н.к. - и G ст - масса соответственно крыши и одной стойки;
n - число стоек;
r - радиус крыши.
Прогиб крыши под действием нагрузки q будет
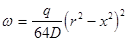
где D - цилиндрическая жесткость
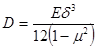 ;
;
х - текущая координата радиуса с началом в центре крыши.
Максимальный прогиб крыши будет (при х = 0)
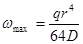 (24)
(24)
или при коэффициенте Пуассона 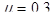 (для стали)
(для стали)
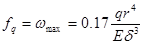 (25)
(25)
где 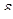 - толщина крыши.
- толщина крыши.
Конструктивный прогиб для стока воды к водоприемникам
fk = 0,01r
Таким образом, суммарный прогиб
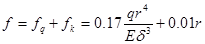
Нагрузка на опорную стойку для понтонного кольца приближенно
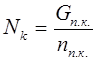
где Gn . к - масса понтонного кольца;
n п.к - число стоек под кольцом.
Напряжения в стойке
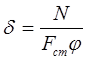
где F ст - площадь поперечного сечения стойки;
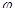 - коэффициент запаса устойчивости (для стоек под понтонным кольцом
- коэффициент запаса устойчивости (для стоек под понтонным кольцом 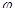 определяют с коэффициентом приведенной длины).
определяют с коэффициентом приведенной длины).
Задавшись величиной местного прогиба крыши, можно определить расстояние между стойками. Обозначим расстояние между концентрическими окружностями, по которым размещены стойки, а. Тогда прогиб между ними будет:
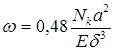
где 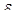 толщина крыши;
толщина крыши;
Nк - нагрузка на одну стойку.
В среднем расстояние между стойками в радиальном и кольцевом направлениях (по хорде) принимают равным 1000 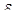 , не более, округляя эту величину до ближайшего целого (по числу стоек).
, не более, округляя эту величину до ближайшего целого (по числу стоек).
Дата: 2019-05-28, просмотров: 292.