Процессы поверхностного упрочнения требуют применения концентрированного источника нагрева с плотностью теплового потока на поверхности материала 103 - 106 Вт/см2 . Основным фактором, отличающим плазменный нагрев от лазерного нагрева, является механизм взаимодействия источника энергии с материалом. При лазерном нагреве световой поток излучения, направленный на поверхность материала, частично отражается от нее, а частично проходит в глубь материала излучение. Излучение, проникающее в глубь материала, практически полностью поглощается свободными электронами проводимости в приповерхностном слое толщиной 0,1 - 1 мкм [1]. Поглощение приводит к повышению энергии электронов, и вследствие этого, к интенсификации их столкновений между собой и передаче энергии кристаллической решеткой металла. Тепловое состояние металла характеризующееся двумя температурами: электронной Те и решеточной Тi , причем Те» Тi. С течением времени (начиная со времени релаксации tР ~ 10-9с) разность температур Те- Тi становится минимальной и тепловое состояние материала можно охарактеризовать общей температурой Тм. Дальнейшее распределение энергии вглубь материала осуществляется путем теплопроводности.
Нагрев поверхности материала плазменной струей осуществляется за счет вынужденного конвективного и лучистого теплообмена:
(2.1.)
q = q k + qл
Для приближенных расчетов тепловых потоков в поверхности используется модель лучистого и конвективного теплообмена основанная на теории пограничного слоя [2], Плотность конвективного теплового потока определяется из выражения:
(2.2.)
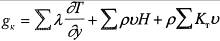
где λ – коэффициент теплопроводности,
Н - энтальпия единицы массы,
Кт - термодиффузионный коэффициент,
у - координата, нормальная к обрабатываемой поверхности.
В общем виде конвективный нагрев поверхности обусловлен переносом энергии плазменной струи под действием теплопроводности, диффузии. На практике используют более простое выражение:
(2.3.)
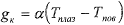
где α–коэффициент теплопроводности
Тплаз - температура плазменной струи на внешней границе
пограничного слоя,
Тпов - температура поверхности.
Связь между α и параметрами плазменной струи выражается через критериальные зависимости (число Нуссельта, Прандля, Рейнольдса и т.д.) выбор для различных случаев взаимодействия плазмы с поверхностью приведен в работах. [2].
Согласно данных работ [3] доля лучистого переноса энергии от плазменной струи к поверхности металла составляет 2-8% от общего баланса энергии. В случае использования импульсной плазменной струи доля лучистого теплообмена возрастает до 20-30%. Лучистый поток к единице площади поверхности в нормальном направлении определяется следующим образом [4]
(2.4.)
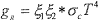
где ξ 1 - интегральная поглощательная способность поверхности,
ξ 2 -степень черноты плазмы
σс - постоянная Стефана-Больцмана
Т -температура плазмы
Учитывая, что теплообмен между струей и поверхностью в основном определяется конвективной составляющей теплового потока, то пренебрегая лучистым теплообменом (за исключением импульсной плазменной струи)
можно рассчитать тепловой поток по выражению Фея-Риддела [5]
(2.5.)
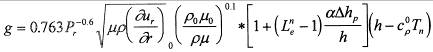
или
(2.6)
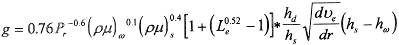
где Рг - усредненное число Прандля,
(ρµ)ω, (ρµ)s - плотность и коэффициент динамической вязкости плазмы при
температурах, соответственно, поверхности тела и внешней границы
пограничного слоя,
Lе - число Льгоса - Семенова,
Ld - энергия диссоциации, умноженная на весовую долю атомов,
соответствующую температуре струи,
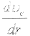 - градиент скорости в критической точке, равный ~ U плазм / d сопла
- градиент скорости в критической точке, равный ~ U плазм / d сопла
hs- полная энтальпия плазменной струи.
При нагреве поверхности металла плазменной дугой (плазмотрон прямого действия), эффективность нагрева возрастает за счет электронного тока q е
(2.7.)
q = q k + qл + qе
Дополнительная тепловая мощность за счет электронного тока рассчитывается из выражения:
(2.8.)
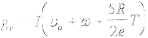
Эффективный КПД плазменно-дугового нагрева на 10-30 % выше, чем при использовании плазменной струи и может достигать 70=85 % [3,6]. Энергетический баланс плазменного нагрева при атмосферном давлении выглядит следующим образом: 70 % - конвективный теплообмен;
20 % - электронный ток;
10 % - лучистый теплообмен.
При использовании плазменной струи (дуги), как источника тепловой энергии, наибольший интерес представляет распределение теплового потока по пятну нагрева. Распределение удельного теплового потока q2в пятне нагрева приближен-но описывается законом нормального распределения Гаусса [7]
q z = q2 m exp (- Kr 2 ) (2.9.)
где К - коэффициент сосредоточенности, характеризующий форму кривой нормального распределения, а следовательно концентрацию энергии в пятне нагрева,
q2m - максимальный тепловой поток.
Коэффициент сосредоточенности играет большое значениев процессах плазменного упрочнения, т.к. - регулирует скорость нагрева поверхностного слоя металла. Максимальная плотность теплового потока в центре пятна нагрева связана коэффициентом сосредоточенности выражением [7]
(2.10.)
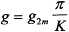
Теплообмен между плазменной струей и упрочняемой поверхностью происходит в области пятна нагрева, условный диаметр которого равен:
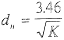
На границе этого пятна нагрева удельный тепловой поток составляет 0.05 % от максимального g 2т [7].
Параметры режима работы плазмотрона оказывают сильное влияние на коэффициент сосредоточенности. С увеличением силы тока К возрастает. Уменьшение диаметра сопла ( d !с≤5) увеличивает К. С увеличением расхода плазмообразующего газа коэффициент сосредоточенности имеет максимум, рис.2.
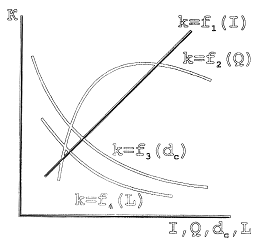
На коэффициент сосредоточенности оказывает большое влияние способ подачи газа, геометрия сопла и электрода. В таблице 2.1. приведены экспериментальные и расчетные величины эффективного КПД нагрева, коэффициента сосредоточенности, тепловой плазменной дуги в зависимости от способа подачи плазмообразующего газа, геометрии сопла и катода. Видно, что переход от максиальной к тангенциальной подаче газа в сопло (при постоянном расходе) увеличивает коэффициент сосредоточенности на 15-40 % при одновременном увеличении эффективного КПД нагрева. Параболическая форма сопла формирует хорошо направленный плазменный поток, по сравнению с другими формами, однако степень сжатия дуги при этом снижается.
Использование кольцевого катода предпочтительнее при тангенциальной подаче газа, т.к. в случае аксиальной подачи нарушается однородность столба дуги
| Диаметр сопла, мм | Длина канала сопла(мм) | U,B | I,A | Способ подачи газа в сопло | Геометрия | Эффективный КПД нагрева, % | Коэффициент сосредоточенности дуги, см. | |
| сопла | катода | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 4,4 | 35 | 100 | тангенциальный | цилиндр | стержень | 68 | 13,2 |
| 2 | 4,4 | 35 | 100 | ------/------ | парабола | ------/------ | 60 | 10,1 |
| 2 | 4,4 | 35 | 100 | ------/------ | раструб | ------/------ | 49 | 6,5 |
| 2 | 4,4 | 35 | 200 | ------/------ | цилиндр | ------/------ | 70 | 15,1 |
| 2 | 4,4 | 25 | 200 | ------/------ | парабола | ------/------ | 63 | 11,8 |
| 2 | 4,4 | 25 | 200 | ------/------ | раструб | ------/------ | 51 | 6,9 |
| 3 3 3 3 | 4,4 3,0 3,0 3,0 | 25 | 200 | аксиальный | цилиндр | стержень | 58 | 10,8 |
| 25 | 200 | ------/------ | цилиндр | ------/------ | 50 | 7,2 | ||
| 25 | 200 | ------/------ | цилиндр | ------/------ | 39 | 4,8 | ||
| 25 | 200 | Аксиально-тангенциальный | цилиндр | ------/------ | 61 | 11,2 | ||
| 4 | 5,0 | 23,5 | 300 | аксиальный | цилиндр | стержень | 63 | 11,5 |
| 4 | 5,0 | 23,5 | 300 | аксиальный | парабола | ------/------ | 54 | 8,1 |
| 4 | 5,0 | 23,5 | 300 | аксиальный | раструб | ------/------ | 50 | 5,1 |
| 4 | 5,0 | 23,5 | 300 | Аксиально-тангенциальный | цилиндр | ------/------ | 70 | 15,2 |
| 5 | 6,2 | 23 | 150 | тангенциальный | цилиндр | кольцо | 50 | 5,9 |
| 56,8 | 24 | 200 | ------/------ | ------/------ | ------/------ | 55 | 6,2 | |
| 5 6,9 | 26 | 300 | ------/------ | ------/------ | ------/------ | 60 | 6,8 | |
| 2 4 | 35 | 150 | тангенциальный | цилиндр | стержень | 65 | 17,8 | |
| 33,5 | 24 | 300 | ------/------ | ------/------ | ------/------ | 60 | 16,8 | |
| 4 6,2 | 28 | 300 | ------/------ | ------/------ | ------/------ | 64 | 17,1 | |
Табл. 2.1.
Влияние способа подачи газа (аргона) в сопло, геометрия сопла и катода на эффективный КПД нагрева и коэффициент сосредоточенности плазменной дуги
Геометрия сопла
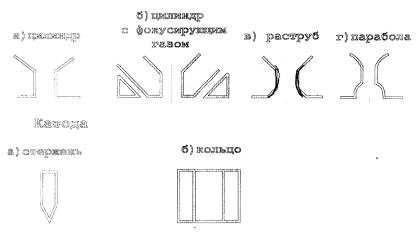
по сечению сопла. При использовании сопла с фокусирующим газом коэффициент сосредоточенности увеличивается. От степени обжатия столба дуги зависят энергетические характеристики плазмотронов (напряжение дуги, эффективная тепловая мощность, концентрации теплового потока и др.), [26,27]Так сжатие дуги, горящей в аргоне при силе тока 150-200Д-А (за счет изменения диаметра сопла и его положения по длине вольфрамового катод а), привело к увеличению напряжения дуги и напряженности электрического поля в столбе дуги, рис,2.2.

Рис.2.2. Распределение теплового потока дуги g( r) по радиусу пятна нагрева малоамперной дуги в зависимости от степени сжатия [ 26]. 1-свободно горящая электрическая дуга;
Дата: 2019-05-28, просмотров: 367.