Избыточность видеоинформации может быть описана функцией корреляции между отсчетами изображений; она проявляется в высокой степени взаимной статистической прогнозируемости близколежащих отсчетов, взятых из изображения. Конечной целью операции сжатия видеоинформации является устранение этой статистической прогнозируемости (т.е. необходимо в максимально возможной степени уменьшить коррелированность отсчетов). На блок-схеме рис. 4.7 показаны основные операции, выполняемые системой сжатия видеоинформации. Сначала выполняется операция по максимальному уменьшению коррелированности отсчетов изображения. Затем отсчеты должны быть соответствующим образом квантованы. Квантованные отсчеты кодируются в форму, благоприятную для передачи (при этом, конечно, может быть обеспечена возможность обнаружения или исправления ошибок) .

Квантование и кодирование выполняются с учетом общих правил, не зависящих от особенностей схемы декорреляции, выбранной для первого этапа обработки. Поэтому системы сжатия видеоинформации различаются видом схемы, выполняющей операции, относящиеся к первому этапу. В силу этого способам реализации первого блока схемы рис. 4.7 здесь будет уделено больше внимания, чем вопросам

Рис. 4.7. Блок-схема системы сокращения избыточности

          видеоинформации.

построения второго и третьего блоков. Такой подход полностью соответствует замыслу данной книги, посвященной техническим применениям цифровой обработки сигналов, т.е. задачам, в основном относящимся к первому блоку.

При разработке принципов реализаций первого блока схемы рис. 4.7 следует учесть ряд соображений. Рассмотрим сначала статистические свойства изображений. Если отсчеты изображения образуют сетку точек размером N N и каждый отсчет представлен Р - разрядным двойным числом, то при записи и передаче изображения с помощью обычной импульсно-кодовой модуляции (ИКМ) потребуется N ² P двоичных разрядов. Однако, как было отмечено выше, типичное изображение имеет большую избыточность. Один из способов, позволяющих измерить эту избыточность и сравнить ее с номинальным числом N ² P разрядов, заключается в построении гистограммы яркости изображения и вычислении соответствующей энтропии. С помощью Р- разрядных чисел можно описать квантованяе по 2^p уровням. Для этого следует проанализировать все N ² отсчетов и подсчитать, сколько раз встречается каждый уровень квантования. Затем следует построить гистограмму яркости изображения, т.е. для каждого уровня квантования указать число его появлений в изображения. Разделив эти числа на общее число точек N ² , можно получить аппроксимацию плотности вероятности процесса, порождающего изображение. Если обозначить нормированные частоты через p_i ( i = 1, 2, ... , 2^p ), то энтропия по определению выражается суммой

         h = 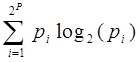^__                                 (4.19)

и равна средней информации (измеряемой числом бит, приходящихся на элемент изображения), содержащейся в каждом элементе изображения. Анализ изображений показал, что типичное значение h гораздо меньше числа разрядов Р, необходимого для стандартного представления с помощью ИКМ. В работе [20] отмечалось, что энтропия имеет величину порядка 1 бит/точка. Это означает, что разрядность массива, описывающего изображение, можно (хотя бы теоретически) сократить без потерь информации в среднем до 1 бит/точка.

Энтропия служит мерой статистической избыточности, но не дает сведений о ее происхождении. Источником избыточности, как подсказывает наблюдателю его зрение, является высокая степень однородности изображения на малых участках. Эту пространственную избыточность можно определить с помощью ковариационной матрицы изображения. Сначала лексикотрафически преобразуют матрицу из N N отсчетов изображения в N ² - компонентный вектор [т.е. элементы первой строки (или столбца) матрицы g ( j , k ) становятся компонентами вектора с номерами от 1 до N , элементы второй строки (столбца) — компонентами с номерами от N+1 до 2 N и т.д.]. Затем вычисляют ковариационную матрицу изображения

   [ C_g ] = E { ( g - E ( g ))( g - E ( g )) ^T } ,                     (4.20)

где Е - среднее значение но ансамблю, a g - вектор, построенный из отсчетов изображения. На практике редко оказывается возможным проводить усреднение по ансамблю и ковариационную матрицу получают с помощью оценки пространственной корреляции [21].

Ковариационные структуры, такие, как матрица [ C_g ], не имеют взаимно - однозначной связи с исходным изображением. Коул [21] показал, что многие неодинаковые изображения могут оказаться весьма сходными в ковариационном (или спектральном) смысле. Следовательно, имеются основания для замены сложной матричной структуры типа [C_g ] более простой. В частности, рассматривалось (см., например, работу [22] ) применение модели с авторегрессионным марковским процессом п-_го порядка, где п обычно невелико (например, n = 3). Тот факт, что подобные модели оказываются корректными, и применение их оправдано при анализе методов сжатия информации, таких, как дифференциальная импульсно - кодовая модуляция (ДИКМ), указывает на высокую степень взаимосвязи между соседними участками изображения.

При сжатии видеоинформации кроме статистических свойств изображения весьма важно учитывать и особенности получателя изображений. Зрение человека обладает ограниченными возможностями и характеризуется некоторыми известными (отчасти) отличительными особенностями. Использование, конкретных особенностей зрения для сокращения избыточности изображений называется психофизической обработкой. Известно, например, что при восприятии яркости света, попадающего в глаз, зрительная система ведет себя как нелинейная система с логарифмической характеристикой. Кроме того, система зрения человека не чувствительна к очень высоким или очень низким пространственным частотам, а в области средних частот ведет себя почти как полосовой фильтр, что обусловлено торможением нервных клеток сетчатки глаза. Нелинейность и частотная зависимость чувствительности зрительной системы позволили создать оптимальные системы сжатия видеоинформации. В этих системах для достижения большей устойчивости к ошибкам, появляющимся при кодировании и передаче, изображение обрабатывается примерно так же, как и в зрительной системе человека. Впервые это предложение было сделано Стокхэмом [23].

Сокращение избыточности информации математически строго обосновывается положениями теории кодирования при заданном критерии точности [24]. Как отмечали Маннос и Сакрисон [17], эффективные теоремы теории кодирования при заданном критерии точности в задачах сжатия видеоинформации применить не удалось. Основной причиной этого явилась сложность выбора критерия допустимой величины ошибок, согласующегося со свойствами системы зрения человека. Манное и Сакрисон смогли показать, что можно пользоваться критерием, связанным с нелинейными и пространственно-частотными свойствами зрения. Их работа имеет очень важное значение для дальнейшего развития методов сокращения избыточности изображений. Введение подходящей предварительной обработки во всех схемах, которые будут рассмотрены ниже, может значительно улучшить качество работы систем сжатия видеоинформации.