Как было отмечено выше , точное восстановление сигнала возможно только при строго ограниченном спектре сигнала и при использовании идеального ФНЧ .НА практике мы имеем дело с сигналами конечными во времени, т.е. бесконечным , теоретически , спектром и для восстановления используем реальные ФНЧ . Рассмотрим ошибки восстановления , вызванные реальностью сигнала (сигнал ограничен во времени , т.е. не ограничен по частоте ). Основная энергия сигнала сосредоточена в диапазоне частот до Fm и только малая доля будет выходить за Fm .
1)На основании т. Котельникова мы не можем восстановить спектральные составляющие , лежащие выше частоты Fm .
2)В спектре восстановленного сигнала появяться дополнительные составляющие , представляющие собой зеркальное отображение " вниз " по частоте спектральных составляющих сигнала относительно оси совпадающей с частотой среза идеального ФНЧ и равной Fm .Поясним
это на рисунке: фнч
S f(f) S1(f) S2(f) S3(f)
0 Fm 3Fm f
Огибающая спектральной плотности сигнала f(t) представляет собой функцию S1(f) . Спектр отсчетных импульсов SDf(f) представляет собой периодически повторяемую функцию S1(f) с периодом 2Fm . Идеальный ФНЧ с частотой среза Fm не пропускает составляющие основного сигнала и пропускает составляющие сектра амплитудно-модулируемой первой гармоники спектра отсчетных импульсов (2Fм) .
3)При восстановлении сигнала конечной длительности следует иметь ввиду что :
а) точность восстановления в средней части сигнала будет наибольшей, а по краям наименьшей;
б) в моменты , соответствующие отсчетам сигнал восстанавливается точно, а в средней части между отсчетными моментами ошибка максимальна
ВЫБОРКИ ИЗ АНАЛОГОВОГО СИГНАЛА.
Схема взятия выборки из аналогового сигнала.
1-Умножитель
2-Схема хранения УВХ
3-Квантователь
4-Преобразователь АЦП
5-Регистр
УВХ-устройство выборки и хранения. Перед умножителем стоит фильтр для уменьшения помех. Квантователь находит ближайший оцифрованный уровень. Устройство хранения дает время квантователю для принятия решения. Устройство хранения-конденсатор,окруженный ключами с большим сопротивлением ( т.е.RC-цепочкой с малой емкостью).Постоянная времени t стремится к единице, это переходный процесс в цепочке (т.е. конденсатор заряжается). За время Dt изменение сигнала мало,т.к. очень большое входное сопротивление преобразователя.Это и есть хранение. Преобразователь -преобразует вид кода (т.е. переводит его в бинарную систему счисления, за счет пороговых устройств). Регистр-считывает этот код, а за тем последовательно, побитно передает в линию.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
Квантование перидического сигнала.
W=2p/T
cosWT, cos2WT, ... , cosnWT.
n=3 n=Ґ
Много ли W нужно иметь и от чего это зависит (зависит от того насколько
гладкий сигнал).Если ширина спектра периодического сигнала конечно,
то он описывается конечным числом гармоник .N-кол-во отсчетов на один период.
ДПФ строго описывает периодический сигнал с конечным спектром ( если это не
соблюдается ,то появляется ошибка в представлении сигнала ДПФ ).
N-1
Cд(t)=е Ckd(t-kDt), где Т=NDt, Ck=C(kDt).
k=0
Ґ
т C(t)d(t-t)dt=C(t)-фильтрующее свойство d-функции.
-Ґ
Ґ
Cд(t)=е Cn*exp(j2npk/T) Пара преобразований Фурье
-Ґ
T
Cn=1/T тCд(t)exp(-j2npt/T)dt
0
NDt N-1
Сn=1/NDt т е Ckd(t-kDt)exp(-j2npt/T)dt={сжали ось времени symbol 120 \f "Symbol" \s 10xsymbol 61 \f "Symbol" \s 10=t/symbol 68 \f "Symbol" \s 10Dtsymbol 125 \f "Symbol" \s 10=
0 k=0
N N-1 N-1 N
=1/N т е Ckd(x-k)exp(-j2pnx/n)dx=1/N е Ck т d(x-k)exp(-j2npx/N)dx=
0 k=0 k=0 0
N-1
=1/N е Ckexp(-j2npk/N)
k=0
T=NDt
N-1
Cn=1/N е Ck exp(-j2npk/N) Пара дискретного преобразования Фурье
k=0
N-1
Ck= е Cn exp(jk2np/N)
0
Cn-комплексная гармоника, а N-кол-во отсчетов.
СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ.
1. Линейность - если в цепи отклик на сумму воздействий равен сумме откликов.
Спектр суммы сигналов равен сумме спектров сигналов.
N-1
Ck= е Сxn exp(j2npk/N)
0 Выборки двух сигналов.
N-1
Uk= е Cyn exp(j2npk/N)
0
Zk=Ck+Uk , Линейность преобразования Фурье
Сzn=Cxn+Cyn ( для интегралов и сумм).
2. Для дискретного сигнала кол-во отсчетов спектра ( Сn) равно кол-ву
отсчетов сигнала.
3.Коэффициент (Со) дает постоянную составляющую.
N-1
Со=1/N е Ck ѕ это математическое ожидание.
k=0
4. Если N-четное ,то тогда
N-1 k
Cn/2=1/N е Ck(-1)
k=0
5. Если Ck - вещественные, то Cn ,расположенные симметрично
относительно Cn/2 образуют комплексно сопряженные пары.
N-1 N-1 +
C =1/N е Ck exp(-j2pk(N-n)/N)=1/N е Ck exp(j2kp/N)=Cn
N-n k=0 k=0
Отсчеты выше C повторяют спектр от Co до C .
N/2 N/2
Но мы не нарушаем теорему Котельникова, т.к. Сn комплексное число,
оно требует два числа для своего представления. Следовательно нужно
ровно N отсчетов ,как и по Котельникову ( N=2FT=T/Dt).
ЦАП и АЦП.
1 3 5
4
2 ЦАП АЦП 2
 |
+5в +15в +5в
6 7 6
1.Стробирующий импульс ( аналоговая величина, соответствующая дис-
кретному слову).
2. N-разрядное дискретное слово (код).
3.Опорное аналоговое напряжение (определяет от какого сигнала ведется
счет т.е. служит для получения единиц измерения в дискретных долях).
4.Аналоговый сигнал.
5.Пуск (внешний сигнал - для конкретного момента времени будет получен
код).
6.Логическое питание.
7.Аналоговое питание.
Отдельные земли обеспечивают подавление импульсных помех ( т.е.возрастает
помехоустойчивость) по питанию.
Входные и выходные сигналы ЦАП и АЦП.
Сигналы ЦАП АЦП
аналоговый на выходе ; напряжение вход ; напряжение ; полярность ;
или ток ; полярность ; ве- величина ; ( есть однополярные
личина ( бывают одно- и двуполярные АЦП ) ;
и двуполярные ЦАП ) (2.5В , 5В , 10В , 10.24В , 20В)
(2.5В,5В,10В,10.24В,20В)
(1мА,1.2мА,1.5мА,2.5мА)
цифровое вход ; послед. или парал. выход ; последовательный
слово ( шина ) включение ; или параллельный ;
логические уровни :
ттл-5В ; эсл- -5В,-2.5В ;
кмоп-3В,15В ; источник
питания : анал.±15,±12В ;
дискр.+5В .
сигналы стробирующий импульс а) входной импульс начала
управления ( при завершении ввода преобразования.
слова , т.е. тактовый ввод) б) вых. “состояние”
( говорит , что на выходе
появился код )
Dt между сигналами а
и б - это врнмя , затрачи-
ваемое АЦП на преобра-
зование.
опорный эталонное напряжение , эталонное напряжение ;
относительно которого внешнее , внутреннее ;
ведется счет ; можно использавать перемен-
ное
При преобразовании мы можем получать прямой код Uвых. ( 0-10В ), или
двуполярный ( ± 10В ). При использовании ЦАП и АЦП необходимо обра-
тить внимание на используемый код ( т.к. они различны ).
Однополярные : как правило старший разряд обеспечивает 0,5 Uопор. ,
n
следующий разряд 0,25 Uопор. , ... , младший 1/ 2 Uопор. .
Двуполярные : первый разряд дает знак , следующий 0,5 Uопор. ,
n-1
младший 1/2 Uопор. .
-0,51 ё -0,38 ® 000 Декодирование аналогового
-0,38 ё -0,26 ® 001 напряжения в бинарное число
-0,26 ё -0,13 ® 010 DU = 0,128 - шаг квантования.
-0,13 ё 0 ® 011 Uразмаха = 1,024 В.
0 ё 0,13 ® 100 ( ошибка не больше 0,5 DU ).
0,13 ё 0,26 ® 101
0,26 ё 0,38 ® 110
0,38 ё 0,51 ® 111
ОСНОВНЫЕ ТИПЫ ЦАП.
1.Цепочка взвешенных резисторов.
R R Rвх.оу№0 ,Rключей№0 (удается реали-
зовать ключи с сопротивлением R»10 Ом)
2R Uвых~еIвх
4R Недостатки:
ОУ Слишком большой разброс сопротивлений
8R Uвых и как следствие трудность в изготовление
их на одной микросхеме .
Влияние Rвх.оу на цепь.
Uопорное
2.Цепочка R-2R .
+Uопорн
2R Uвых Достоинства:
Более технологична ,т.к.всего два
номинала сопротивлений.
-Uопорн 2R R Rн
2R R
2R R
2R
АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ.
А).АЦП последовательного приближения (скоростные).
xi(t) УВХ Ком- схема Umax
пар. управл Uвх
1/2Umax
ЦАП RG
Uвых Umin
цап n
вых 1 2 3 4 5
1.При подачи пускового импульса , после УВХ обнуляется регистр (RG),
затем в старший разряд регистра дается “1”,на выходе ЦАП появляется
напряжение равное 0.5Umax .Если Uвых.увх>Uвых.цап ,то ”1” в старшем
разряде остается ( иначе она стирается ).
2.Опять ставят “1” в следующий разряд регистра .......................................
.......................................................................................................................
Кол-во шагов соответствует кол-ву разрядов АЦП.
Б).АЦП параллельного действия .
Uопорн. В качестве опорного на каждый
компаратор (К) подается сетка
УВХ R напряжений - Uопорн.
xi(t) K n
2 n
R Kол-во компараторов = 2 .
K При подачи сигнала на вход АЦП ,
R ДЕКО- все компараторы у которых
K ДЕР Q2 Uопорн.<Uвх.
дадут единици.
R Q1 Наивысший номер компаратора
K находящегося в единичном состоя-
R Q0 нии соответствует выходному коду
K АЦП.
R Недостатки:
K Эти АЦП малоразрядные (4-5)
R (т.к.необходимо много компара-
K торов).
R
K
R
КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ.
x t)= x(t)+jh(t)=E(t)exp{ jy(t)} x(t) x
` `
h(t)
пре-
образ.
При определенных правилах связи комплексное число дает аналитический сигнал
( т.е. непрерывный вместе со своими производными ) .
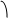h(t)
E(t) Описание сигнала через огибающюю E(t)
и фазу y(t) .
y(t)
0 x(t)
x(t)=Re{x(t)}=E(t)cosy(t)
`
Нам нужно установить правило выбора сомножителей E(t) и cos(y(t)) т.к.
если мы узнаем один , то легко найдем другой .
Понятие огибающей очень расплывчато , поясним это на примерах :
( ) -огибающие для одного процесса
разные .
Первый дал понятие огибающей и фазе Гильберт , он дал определение
мнимой составляющей ( т.е. ввел комплексные величины ) .
Ґ
(t)=1/p тxi(t )/ t-t dt
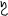Пара преобразований -Ґ
Гильберта Ґ
x(t)=1/p т h(t)/ t-t. dt
-Ґ
Преобразование Гильберта - широкополосный фазовращатель , оно
поворачивает все спектральные составляющие на 90° .
ѕѕѕѕѕ
E(t)= Ц x(t) + h(t) - огибающая понятия применимые
для любого сигнала .
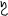y(t)=arctg[ (t)/ x(t)] - фаза
w(t)=dy(t) - частота
dt
x(t)=Acosw t ; h(t)=Asinw t ( т.е. h(t) получается приповороте x(t)
на 90° ).
x(t)= Acosw t +Asinw t = A
Схема получения АМ ОБП .
l 1/2cos(w -l)t+1/2cos(w +l )t
 | |||
 | |||
x(t) x(t)cosw t
генератор
cosw t
cos(w - l)t
+
j=p/2 j=p/2
 |
sinlt sinw t h(t)sinw t
1\2cos(w - l)t- 1/2cos(w +l)t
+ Получили АМ ОБП без использования фильтров .
Мы оперируем комплексными функциями для того
чтобы убрать основную часть энергии несущей .
Огибающие и фаза УПСП (узко-полосного случайного процесса ).
Квадратурные составляющие огибающей .
Dw<<w
460 465 470 f,кГц
y(t) = w0t- j(t)
w0 - ( ) j(t)
y(t)- ( )
t t
Фаза УПСП разбивается на две составляющие флуктуированную j(t)
и мат.ожидания w0t .
x(t) =Е(t)cosy(t)=E(t)cos(w0t -j(t))=E(t)cosj(t)cosw0t+E(t)sinj(t)sinw0t
A(t) B(t)
A(t) и B(t) медленно меняющиеся функции . Получаются , как случайные
функции времени .
x(t)=A(t)cosw0t + B(t)sinw0t , где A(t) и B(t) - квадратурные составляющие
огибающей .
В этом колебание вектор Е(t) будет колебаться , т.е. показывать флуктуацию.
A(t)
E(t)
j(t)
B(t)
Свойства функций :
1. Энергетические спектры G (w) иG (w) одинаковые .
2. Законы распределения одинаковые w (x)=w (x)=wa(x)=wб(x).
3. Коррелляционные функции равны Bx(t )=B (t ) .
4. Справедливо свойство ортогональности .
ѕѕѕѕ ѕѕѕ
h(t)x(t)=0 A(t)B(t)=0
5.-Ґ <=A(t) < Ґ ; -Ґ <=B(t)<Ґ;E(t)>=0 .
ѕ ѕ
6. Если Гауссовский шум то A(t)=0 и B(t)=0
( Т.е. нулевые мат. ожидания ) .
Если A(t)=F то это значит что в случайном процессе
появилась детерменированная ф-ия .
x(t)=A(t)cosw0t + B(t)sinw0t+ Fcosw0t
 | |||||
 | |||||
 | |||||
7. A (t)=B (t) =Gx - мощность реализации .
ѕ ѕ ѕ
E (t)= A (t)+B (t) =2Gx - мощность огибающей .
8. Ba(t)=Bб(t) ( т.к. скорости изменения одинаковы )
9. Bx(t)=Ba(t)cosw0t
ДИСКРЕТНАЯ СВЕРТКА.
Ґ
f(t)=тC(t)y(t-t)dt - Свертка -интеграл Дюамеля (прохождение
-Ґ сигнала через нелинейную инерционную
цепь)
N-1
fm=1/N* е CkUm-k - Свертка дискретных сигналов.
k=0 m=0,1,2,3,...,N-1.Т.к.число отсчетов описывающее
сигнал Х(t) ,будет описывать и функцию fn.
N-1
Ck=еСxn exp(j2pk/N) ;Cxn-амплитуда “n”-ой гармоники спектра.
n=0
N-1
Ym-k=е Cyl exp(j2pk/N)
l=0
N-1 N-1 N-1
fm=1/N е [ е Cxn exp(j2pk/N)][ е Cyl exp(j2pl(m-k)/N)]=
k=0 n=0 l=0
N-1 N-1 N-1
=1/N е е CxnCyl exp(j2plm/N) е exp(j2p(n-l)k/N)
n=0 l=0 k=0
N-1
При n=l , е exp(j2p(n-l)k/N)=N (Если n№l ,то сумма равна “0”).
k=0
Тогда получаем:
N-1
fm= е Cfn exp(j2pmn/N) ,где Cfn=CxnCyn
n=0
Если в одном из пространств пары преобразования Фурье мы
производим умножение ,то во втором пространстве будет про-
изводиться свертка .Это требуется для анализа длинной после-
довательности ,где легче перемножить спектры ,а потом взять
обратное преобразование Фурье .
Ck 2 2 2 Yk 3
2
1
 | | ||||||||
| | |||||||||
 | |||||||||
 | |||||||||
| | |||||||||
-1 0 1 2 -1 0 1 2
CmY(0-m) еXmY(1-m)
еXmY(2-m) еXmY(3-m)
еXmY(4-m)
fm
12
6
0 1 2 3 4 m
Дата: 2019-05-28, просмотров: 267.
