Видеоинформации
Поскольку часто изображения состоят из многих последовательно появляющихся кадров (как, например, в телевидении) и изображение от кадра к кадру меняется мало, то в будущем, по видимому, больше внимания будет уделяться межкадровому сжатию (в отличие от внутрикадрового). Как отмечалось ранее, схемы межкадрового сжатия методом ДИКМ уже изучались. Оказалось, что комбинация внутрикадрового и межкадрового кодирования (в тех случаях, где это возможно сделать) может привести к уменьшению объема передаваемой информации в 30—50 раз.
Интерес к цветным изображениям возрастает; уже проводились опыты по сокращению их избыточности методом ДИКМ и методом преобразования [33, 36]. Методы сжатия аналогичны рассмотренным выше, но их реализация усложняется из-за наличия трех цветовых сигналов.
В последнее время созданы гибридные системы сжатия. В них для сжатия по одной координате (обычно по строкам дискретизованного изображения, или по горизонтали) используется схема с преобразованием, а по другой координате (по столбцам, или по вертикали) - схема с ДИКМ. В результате получается более простая система ( b ней не требуются двумерные преобразования), но дающая такую же или лучшую эффективность кодирования, чем системы с ДИКМ или с преобразованием [20].
Отметим, наконец, что все рассмотренные выше схемы не являются адаптивными, т.е. в них не изменяются в зависимости от свойств изображения распределение кодовых разрядов, расположение уровней квантования и т.д. Тешер [37] показал, что за счет адаптивности можно дополнительно повысить эффективность кодирования изображений. При одинаковом качестве восстановленного непрерывного изображения ему удалось сократить объем передаваемой информации почти вдвое по сравнению с другими системами.
Повышение резкости изображений
Задача любой системы, формирующей изображение, состоит в создании резкого, чистого изображения, свободного от искажений. Это не всегда возможно сделать. Во-первых, каждая реальная система формирования изображений обладает определенными ограниченными возможностями; импульсный отклик реальной системы имеет конечную ширину, что приводит к неизбежному снижению разрешающей способности. Если на изображении необходимо выделять важные детали, размер которых близок к ширине импульсного отклика, то необходимо бороться с потерями разрешения. Так, например, с межпланетных космических аппаратов приходят снимки замечательного качества (особенно, если учесть, откуда они получены), но ученые, изучающие планеты, всегда пытаются увидеть на них элементы поверхности планеты, искаженные в силу ограниченного разрешения фотокамер. Во-вторых, изображения могут быть испорчены из-за неудачного стечения обстоятельств. Можно принять все меры предосторожности, чтобы получить высококачественные снимки, но какая-то часть их окажется испорченной либо за счет движения объекта или камеры, либо из-за плохой фокусировки и т.д. Среди плохих снимков всегда находятся столь важные или настолько редкие, что стоит пытаться их исправить. Устранение искажений относится к задачам повышения резкости (или восстановления ) изображений.
Ниже читатель увидит, что для решения задачи восстановления (или повышения резкости) изображения предложено несколько различных .методов. Для решения же рассмотренной в предыдущем разделе задачи сокращения избыточности изображений было представлено только два существенно различных метода. Как будет показано, восстановление изображений является задачей, не имеющей единственного решения, что и привело к многочисленным попыткам найти лучший способ решения.
Важные аспекты задачи повышения резкости
Изображений
Как показано выше, основное уравнение формирования изображения имеет вид
g ( x , у)= 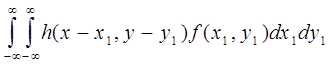
 , (4.34)
, (4.34)
где g - сформированное изображение, h - импульсный отклик или аппаратная функция, а f - функция распределения яркости объ- 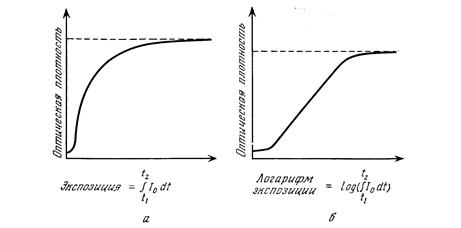
Рис. 4.11.
а - зависимость оптической плотности от экспозиции; б - зависимость оптической плотности от логарифма экспозиции.
екта. Конечно, непосредственно изображение g наблюдатель не получает; изображение существует в виде модуляции интенсивности какого-то излучения, исходящего от объекта. Изображение становится известным только после того, как оно будет воспринято и записано некоторым образом (например, на фотопленке, сетчатке глаза, люминесцентном экране). В процессе восприятия и записи в изображение вносятся шумы, поскольку при любом способе записи сигналов присутствуют шумы записывающей системы. Весь процесс получения изображения, т.е. формирование изображения, его восприятие и запись, был показан в виде блок-схемы на рис. 4.3. Таким образом, восстанавливать изображение приходится по записи, содержащей шум.
Задача повышения резкости изображения усложняется особенностями записывающей системы и ее собственным шумом. Как отмечалось в разд. 4.2, наиболее распространенная система для записи изображений, фотопленка, имеет нелинейную характеристику и вносит шум, модулированный сигналом. Типичная характеристика фотопленки приведена на рис. 4.11,а, где показана зависимость оптической плотности, определенной выше, от интенсивности падающего излучения, причем предполагается, что за .время выдержки интенсивность не изменяется. Обычно такую информацию приводят па графиках с логарифмическим масштабом по оси абсцисс (рис. 4.11,б); получающийся в таких координатах график зависимости D от log Е имеет линейный участок. Вид этой кривой иногда порождает заблуждения относительно резкой нелинейности характеристики фотопленки. Поскольку изображение записывается на пленке зернами серебра, а плотность серебряного слоя пропорциональна оптической плотности, то очевидно, что процессы записи на фотопленку нелинейны по своей сути.
Столь же сложны процессы, создающие шумы пленки. Дисперсия шума, вызванного случайным размещением зерен серебра на пленке, пропорциональна локальной .плотности проявленных серебряных зерен, причем функция пропорциональности усложняется наличием степенного множителя [8]. Таким образом, шум представляет собой флуктуации оптической плотности записи изображения, зависящие от сигнала. В общем случае задача цифровой обработки сигналов с шумом, зависящим от сигнала, еще не решена. Немногочисленные известные результаты [10] указывают, что зависимость шума от сигнала может оказаться не слишком большой проблемой. Поэтому обычно предполагают, что шум создается независимыми от сигнала флуктуациями плотности. Однако логарифмическая зависимость между оптической плотностью пленки, запечатлевшей изображение, и интенсивностью падающего на пленку излучения усложняет задачу. Даже если предположить, что флуктуации оптической плотности не зависят от сигнала, в свете, прошедшем через пленку, будет присутствовать мультипликативный шум, зависящий от сигнала. Аналогичные эффекты наблюдаются в фотоэлектронных системах (типа телевизионных и им подобных), характеристики которых описываются степенным законом.
С учетом вышеизложенного полная модель процессов формирования и записи изображения описывается соотношением
g(x,y) = s [ 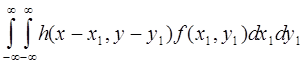 ] +
] +
+ n ( x, y ) (4.35)
где g - фактически записанное изображение, s - характеристика записывающего процесса, а п — шум. Предполагается, что п не зависит от записанного изображения. Задача повышения резкости (или восстановления) изображения заключается в определении исходного распределения интенсивности излучения объекта f ( x , у) на основе записи g ( x , у), содержащей шум.
Формула (4.35) позволяет оценить сложность задачи восстановления изображения. Искажения исходного изображения изменяют интенсивность экспонирующего света, а в нашем распоряжении имеется только нелинейная функция от этих интенсивностей. Если избавиться от нелинейности с помощью преобразования, обратного к s , то получим
s-1 { g ( x, y ) = s-1 {s [ h ( x, y ) ** f( x, y )] + n ( x, y )} , (4.36)
где знак ** означает двумерную свертку. Поскольку обратная нелинейность воздействует на сумму и оператор этой нелинейности недистрибутивен по отношению к оператору сложения, то наличие шумового слагаемого означает, что 1) получить точное обратное преобразование и исходные интенсивности невозможно, 2) при преобразовании g с использованием характеристики, обратной к нелинейной характеристике системы записи, будет получена нелинейная комбинация сигнала и шума.
Решения уравнения (4.36) в настоящее время не получены. На практике при восстановлении изображений делают одно из двух предположений. Первое предположение состоит в том, что в соотношении (4.36) операцию s-1 можно применить к слагаемым ïî отдельности, т.е.
s -1{ g( x, y) } 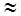 h (x, y) ** f ( x, y )+ s -1{ n ( x, y ) } , (4.37)
h (x, y) ** f ( x, y )+ s -1{ n ( x, y ) } , (4.37)
что эквивалентно замене шума на новый шумовой процесс s -1 {п}. При втором подходе данные обрабатываются в том виде, как они записаны, т.е. предполагается, что нелинейной функцией s можно пренебречь и
g ( x, у ) 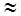 h ( x, у ) у ** f ( x, у ) + п ( x, у ). (4.38)
h ( x, у ) у ** f ( x, у ) + п ( x, у ). (4.38)
Равенства (4.37) и (4.38) были бы справедливы, если бы удовлетворялось любое из двух предположений: 1) функция s имеет слабую нелинейность и ее можно аппроксимировать линейной функцией или 2) сигнал g изменяется b малых пределах (низкоконтрастное изображение) и операторы s и s-1 близки к линейным. Графики типа изображенных на рис. 4.11 показывают, что нелинейность оператора s обычно нельзя считать слабой. При правильном выборе экспозиции диапазон изменения от черного к белому не соответствует предположению о низкой контрастности. Однако на практике изображение удается успешно восстановить в пространстве яркостей, связанном с преобразованием (4.37), или в пространстве плотностей, связанном с преобразованием (4.38), несмотря на теоретические трудности, возникающие при отбрасывании нелинейностей.
Даже при беглом взгляде на соотношения (4.37) или (4.38) видно, что восстановление изображений относится к задачам фильтрации с помощью инверсной свертки (т.е. к обработке записанной информации с помощью оператора h , который является обратным по отношению к оператору двумерной свертки с функцией h). Эта задача сложна тем, что сводится к решению плохо обусловленных систем линейных уравнений [38]. При повышении резкости изображений задача усложняется за счет того, что для многих изображений аппаратная функция сингулярна, т.е. преобразование Фурье от нее имеет нули, что наблюдается, например, при дрожании съемочной камеры или плохой ее фокусировке. Поэтому при решении задач восстановления изображений значительные усилия затрачиваются на преодоление трудностей, связанных с сингулярностью [2].
Для восстановления изображений цифровыми методами необходимо, чтобы все уравнения были записаны для дискретизованных функций. Поэтому соотношение (4.35) принимает вид
g ( j 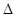 x, k
x, k 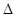 y )
y ) 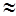 s {
s { 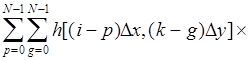
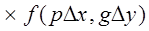 } + n ( j
} + n ( j 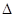 x, k
x, k 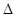 y ) , (4.39)
y ) , (4.39)
где знак (приближения указывает, что дискретные суммы не являются точным представлением исходных интегралов. Аналогичные выражения можно записать для формул (4.37) и (4.38). Интересно отметить, что соотношение (4.39) можно рассматривать как систему уравнений относительно неизвестных значений f. Если выполняются предположения, сделанные при выводе соотношения (4.38), то соответствующие дискретные уравнения (где без потери общности можно положить 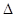 x =
x = 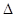 y = 1) прекращаются в систему линейных уравнений относительно f ( p , q ):
y = 1) прекращаются в систему линейных уравнений относительно f ( p , q ):
g ( j, k ) 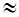
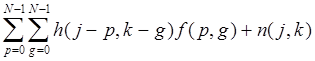 , (4.40)
, (4.40)
Формула (4.40) подсказывает, что задача восстановления изображений сводится к решению системы линейных уравнений. Это действительно так, и для подтверждения можно представить соотношение (4.40) в виде произведения матрицы на вектор. Поэтому значение цифровых методов обработки сигналов, таких, как линейная фильтрация и БПФ, состоит .в том, что они являются средством для быстрого нахождения точного или приближенного решения очень больших (с N 2 переменными) систем линейных уравнений. Такой .подход очень важен для развития более совершенных методов повышения резкости изображений, но обсуждение его требует применения теории матриц в объеме, чрезмерно большом для данной книги. Подробнее связь между матричными представлениями и восстановлением изображений методом дискретного преобразования Фурье описана в работах [2, 39, 40].
Дата: 2019-05-28, просмотров: 347.